nLab limits and colimits by example
Context
Limits and colimits
1-Categorical
2-Categorical
(∞,1)-Categorical
Model-categorical
This entry lists and discusses examples and special types of the universal constructions called limits and colimits.
It starts with very elementary and simple examples and eventually passes to more sophisticated ones.
For examples of the other kinds of universal constructions see
Contents
- Limits and colimits of sets
- Limits and colimits of topological spaces
- Limits and colimits in a preordered set
- Limits and colimits in functor categories
- Colimit of a representable functor
- Examples of limits
- Simple diagrams
- Filtered limits
- In terms of other operations
- Limits in presheaf categories
- Limits in under-categories
- Further resources
Limits and colimits of sets
In the category Set of sets, the concepts of limits and colimits reduce to the familiar operations of
- cartesian product of sets;
- disjoint union of sets;
- subsets defined by equations
- quotient sets of equivalence relations.
Limits
Terminal object
The terminal object is the limit of the empty functor . So a terminal object of is a set such that there is a unique function from any set to . This is given by any singleton set , where the unique function from any set is the function that sends every element in to .
Product
Given two sets , the categorical product is the limit of the diagram (with no non-trivial maps)
This is given by the usual product of sets, which can be constructed as the set of Kuratowski pairs
We tend to write instead of .
The projection maps and are given by
To see this satisfies the universal property of products, given any pair of maps and , we obtain a map given by
More generally, given a (possibility infinite) collection of sets , the product of the discrete diagram consisting of these sets is the usual product . This can be constructed as
Equalizer
Given a pair of functions , the equalizer is the limit of the diagram
The limit is given by a map such that given any , it factors through if and only if . In other words, factors through if and only if . Thus the limit of the diagram is given by
and the map is given by the inclusion.
Pullback
Given two maps and , the pullback is the limit of the diagram
This limit is given by
with the maps to and given by the projections.
While the definition of a pullback is symmetric in and , it is usually convenient to think of this as pulling back along (or the other way round). This has more natural interpretations in certain special cases.
If is the inclusion of a subset (ie. is a monomorphism), then the pullback of along is given by
So this is given by restricting to the elements that are mapped into .
Further, if is also the inclusion fo a subset, so that and are both subobjects of , then the above formula tells us that the pullback is simply the intersection of the two subsets.
Alternatively, we can view the map as a collection of sets indexed by elements of , where the set indexed by is given by . Under this interpretation, pulling back along gives a collection of sets indexed by elements of , where the set indexed by is given b .
General limits
Given a general Set-valued functor , if the limit exists, then by definition, for any set , a function is equivalent to a compatible family of maps for each .
In particular, since an element of a set bijects with maps from the singleton , we have
where is the functor that constantly takes the value . Thus the limit is given by the set of natural transformations from to .
More concretely, a compatible family of maps is given by an element for each , satisfying the appropriate compatibility conditions. Thus, the limit can be realized as a subset of the product of all objects:
Colimits
Initial object
The initial object in is a set such that there is a unique map from to any other set. This is given by the empty set .
Coproduct
(…)
Coequalizer
(…)
Pushout
(…)
General colimits
The colimit over a Set-valued functor is a quotient set of the disjoint union :
where the equivalence relation is that which is generated by
If is a filtered category then the resulting equivalence relation can be described as follows:
(If is not filtered, then this description doesn’t yield an equivalence relation.)
Limits and colimits of topological spaces
We discuss limits and colimits in the category Top of topological spaces.
examples of universal constructions of topological spaces:
Definition
Let be a class of topological spaces, and let be a bare set. Then
-
For a set of functions out of , the initial topology is the topology on with the minimum collection of open subsets such that all are continuous.
-
For a set of functions into , the final topology is the topology on with the maximum collection of open subsets such that all are continuous.
Example
For a single topological space, and a subset of its underlying set, then the initial topology , def. , is the subspace topology, making
a topological subspace inclusion.
Example
Conversely, for an epimorphism, then the final topology on is the quotient topology.
Proposition
Let be a small category and let be an -diagram in Top (a functor from to ), with components denoted , where and a topology on . Then:
-
The limit of exists and is given by the topological space whose underlying set is the limit in Set of the underlying sets in the diagram, and whose topology is the initial topology, def. , for the functions which are the limiting cone components:
Hence
-
The colimit of exists and is the topological space whose underlying set is the colimit in Set of the underlying diagram of sets, and whose topology is the final topology, def. for the component maps of the colimiting cocone
Hence
(e.g. Bourbaki 71, section I.4)
Proof
The required universal property of is immediate: for
any cone over the diagram, then by construction there is a unique function of underlying sets making the required diagrams commute, and so all that is required is that this unique function is always continuous. But this is precisely what the initial topology ensures.
The case of the colimit is formally dual.
Example
The limit over the empty diagram in is the point with its unique topology.
Example
For a set of topological spaces, their coproduct is their disjoint union.
In particular:
Example
For , the -indexed coproduct of the point, , is the set itself equipped with the final topology, hence is the discrete topological space on .
Example
For a set of topological spaces, their product is the Cartesian product of the underlying sets equipped with the product topology, also called the Tychonoff product.
In the case that is a finite set, such as for binary product spaces , then a sub-basis for the product topology is given by the Cartesian products of the open subsets of (a basis for) each factor space.
Example
The equalizer of two continuous functions in is the equalizer of the underlying functions of sets
(hence the largets subset of on which both functions coincide) and equipped with the subspace topology, example .
Example
The coequalizer of two continuous functions in is the coequalizer of the underlying functions of sets
(hence the quotient set by the equivalence relation generated by for all ) and equipped with the quotient topology, example .
Example
For
two continuous functions out of the same domain, then the colimit under this diagram is also called the pushout, denoted
(Here is also called the pushout of , or the cobase change of along .) If is an inclusion, one also write and calls this the attaching space.
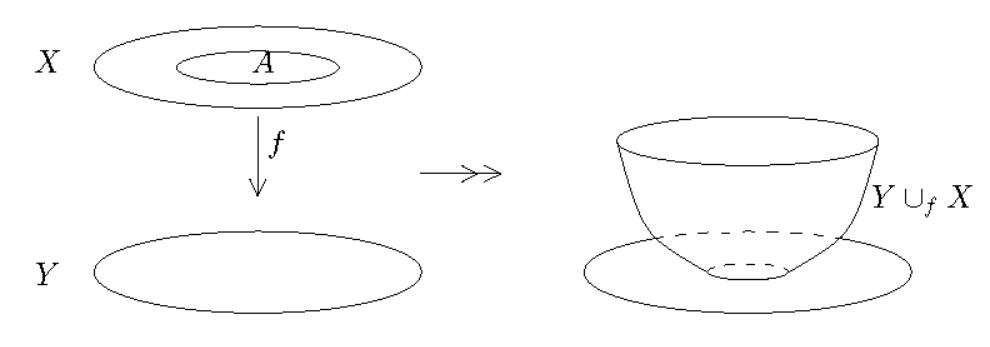
By example the pushout/attaching space is the quotient topological space
of the disjoint union of and subject to the equivalence relation which identifies a point in with a point in if they have the same pre-image in .
(graphics from Aguilar-Gitler-Prieto 02)
Example
As an important special case of example , let
be the canonical inclusion of the standard (n-1)-sphere as the boundary of the standard n-disk (both regarded as topological spaces with their subspace topology as subspaces of the Cartesian space ).
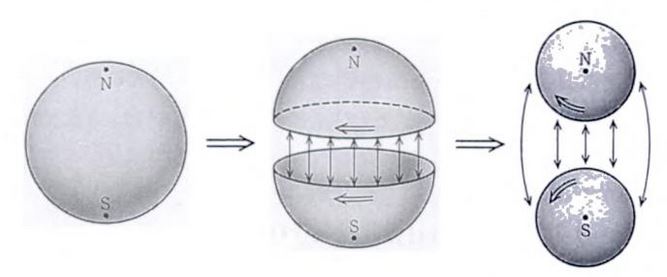
Then the colimit in Top under the diagram, i.e. the pushout of along itself,
is the n-sphere :
(graphics from Ueno-Shiga-Morita 95)
W
Limits and colimits in a preordered set
(..)
Limits and colimits in functor categories
The main point is that limits of functors are computed objectwise. See there for more
Colimit of a representable functor
The colimit of a representable functor (with values in Set) is the point, i.e. the terminal object in Set.
One can readily see this from a universal element-style argument, by direct inspection of cocones.
However, this style of reasoning does not easily generalize to higher category theory. The following gives a more abstract argument that is short and generalizes. We state it in (∞,1)-category theory just for definiteness of notation:
Proposition
(homotopy colimit over a representable functor is contractible)
Let be a small (∞,1)-category and consider an ∞-groupoid-valued (∞,1)-functor which is representable, i.e. in the image of the (∞,1)-Yoneda embedding :
Then the (∞,1)-colimit over this (∞,1)-functor is contractible, i.e. is the point, the terminal object in ∞Groupoids:
Proof
The terminal -groupoid is characterized by the fact that for each we have . Therefore it is sufficient to show that has the same property:
Here the first step is the (∞,1)-adjunction
and the second step is the (∞,1)-Yoneda lemma
Examples of limits
In the following examples, is a small category, is any category and the limit is taken over a functor .
Simple diagrams
-
the limit of the empty diagram in is, if it exists the terminal object;
-
if is a discrete category, i.e. a category with only identity morphisms, then a diagram is just a collection of objects of . Its limit is the product of these.
-
if then is the equalizer of the two morphisms .
-
if has an terminal object (so that is an initial object in ), then the limit of any is .
Filtered limits
-
if is a poset, then the limit over is the supremum over the with respect to ;
-
the generalization of this is where the term “limit” for categorical limit (probably) originates from: for a filtered category, hence a cofiltered category, one may think of as witnessing that is “larger than” in some sense, and is then the “largest” of all these objects, the limiting object. This interpretation is perhaps more evident for filtered colimits, where the codomain category is thought of as being the opposite . See the motivation at ind-object.
In terms of other operations
If products and equalizers exist in , then limit of can be exhibited as a subobject of the product of the , namely the equalizer of
and
See the explicit formula for the limit in Set in terms of a subset of a product set.
In particular therefore, a category has all limits already if it has all products and equalizers.
Limits in presheaf categories
Consider limits of functors with values in the category of presheaves over a category .
Proposition
(limits of presheaves are computed objectwise)
Limits of presheaves are computed objectwise:
Here on the right the limit is over the functor .
Similarly for colimits
Similarly colimits of presheaves are computed objectwise.
Warning The Yoneda embedding does not in general preserve colimits.
Limits in under-categories
Limits in under categories are a special case of limits in comma categories. These are explained elsewhere. It may still be useful to spell out some details for the special case of under-categories. This is what the following does.
Proposition
Limits in an under category are computed as limits in the underlying category.
Precisely: let be a category, an object, and the corresponding under category, and the obvious projection.
Let be any functor. Then, if it exists, the limit over in is the image under of the limit over :
and is uniquely characterized by .
Proof
Over a morphism in the limiting cone over (which exists by assumption) looks like
By the universal property of the limit this has a unique lift to a cone in the under category over :
It therefore remains to show that this is indeed a limiting cone over . Again, this is immediate from the universal property of the limit in . For let be another cone over in , then is another cone over in and we get in a universal morphism
A glance at the diagram above shows that the composite constitutes a morphism of cones in into the limiting cone over . Hence it must equal our morphism , by the universal property of , and hence the above diagram does commute as indicated.
This shows that the morphism which was the unique one giving a cone morphism on does lift to a cone morphism in , which is then necessarily unique, too. This demonstrates the required universal property of and thus identifies it with .
- Remark: One often says “ reflects limits” to express the conclusion of this proposition. A conceptual way to consider this result is by appeal to a more general one: if is monadic (i.e., has a left adjoint such that the canonical comparison functor is an equivalence), then both reflects and preserves limits. In the present case, the projection is monadic, is essentially the category of algebras for the monad , at least if admits binary coproducts. (Added later: the proof is even simpler: if is the underlying functor for the category of algebras of an endofunctor on (as opposed to algebras of a monad), then reflects and preserves limits; then apply this to the endofunctor above.)
Further resources
Pedagogical vidoes that explain limits and colimits are at
Last revised on April 20, 2023 at 17:58:37. See the history of this page for a list of all contributions to it.