Schreiber Towards Quantum Programming via Linear Homotopy Types
-
Towards Quantum Programming via Linear Homotopy Types
talk at
Homotopy Type Theory and Computing – Classical and Quantum,
CQTS @ New York University Abu Dhabi
19-21 April 2024
Abstract. Remarkably, among the -toposes into which HoTT interprets are “tangent -toposes” of parameterized module spectra, which behave like semantics for an enhancement of HoTT by dependent *linear* homotopy types, neatly combining the linear aspect of typed quantum programming languages (like Proto-Quipper) with homotopy-theoretic aspects needed for future *topological quantum* languages. The talk surveys this HoTT-perspective on (topological) quantum systems, developed jointly with Hisham Sati (“Topological Quantum Gates in HoTT” arXiv:2303.02382, “Entanglement of Sections” arXiv:2309.07245, “The Quantum Monadology” arXiv:2310.15735, “Quantum and Reality” arXiv:2311.11035).
Contents
(1) Quantum Systems via Linear Homotopy Types
Following Awodey 2009, it is now well-understood [Cisinski 2012, 2014; Shulman 2015, 2019] that
univalentHoTTfinds its categorical semantics
in -toposes presented by well-behaved (type-theoretic) model categories.
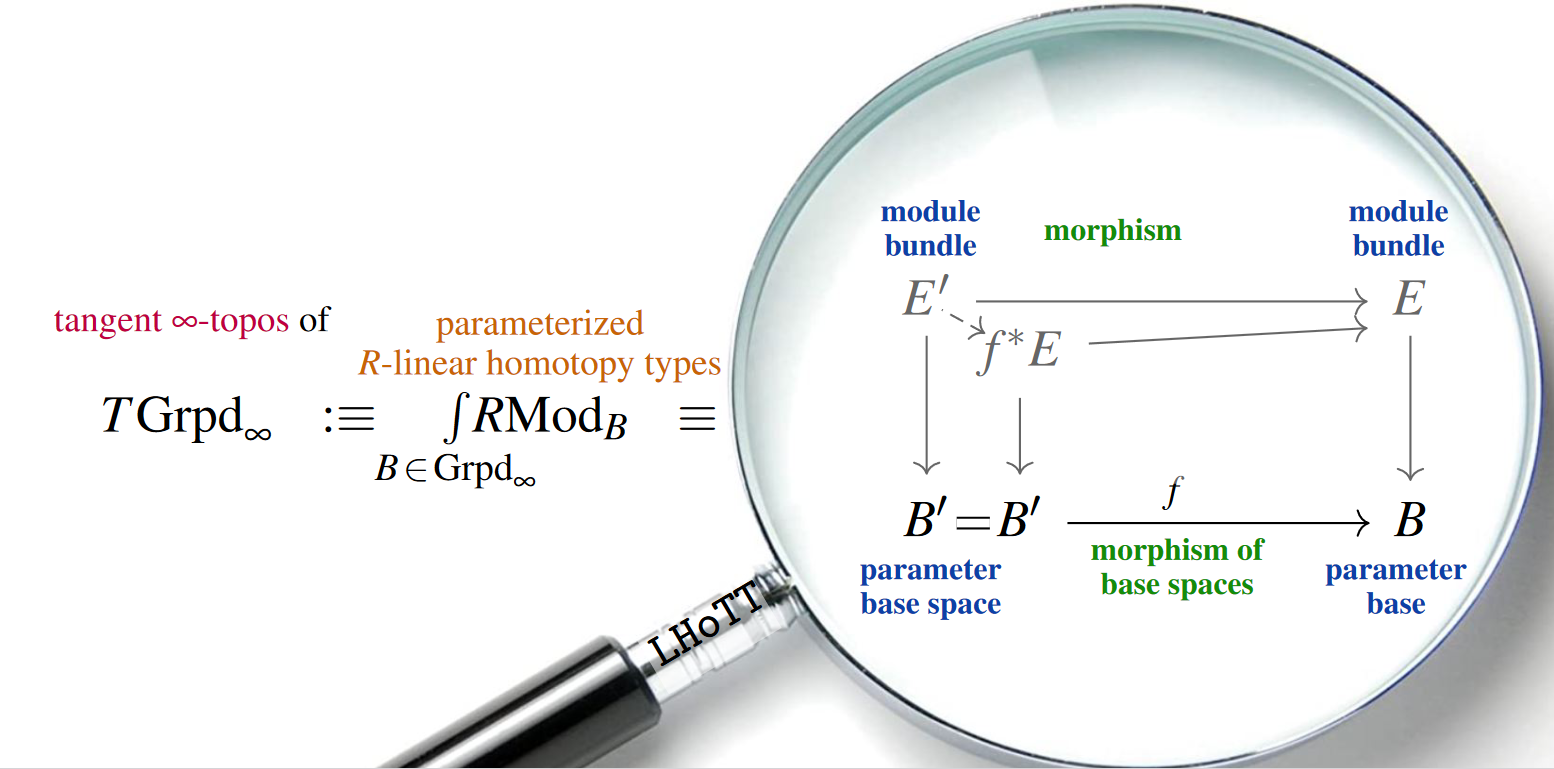
Remarkably [Biedermann 2007; Joyal 2008; Hoyois 2019],
among these -toposes are
of parameterized -module spectra
over varying -groupoids (cf. the talk by Finster).
This can be surprising, because these are amalgamations
of parameterized -module spectra over fixed bases
which as such are far from being -toposes themselves.
This fact can indeed be so surprising that
when I first highlighted it to a HoTT-audience in 2014 (slide 6)
it was ferociously doubted.
Specifically [Robinson 1987; Shipley 2007],
when is the Eilenberg-MacLane spectrum of the complex numbers, say, then
-
is equivalent to flat -vector bundles (aka “-local systems”) over .
More concretely [Sati and S. 2023, Prop. 3.23 p. 40]:
a model category-presentation for
is given by the integral model structure for
the projective model structures of simplicial functor categories
from simplicial groupoids to the model structure on simplicial chain complexes
Alongside its Cartesian product, this category carries
(“external”) symmetric monoidal tensor product-structure :
It turns out [Sati and S. 2023, Thm. 3.42 p. 53, Rem. 344 p. 54],
that this is rather well-behaved
as far as models categories for parameterized spectra go [cf. Malkiewich 2023]
but it is not quite a -monoidal model category-structure.
However [Sati and S. 2023, Thm. 3.46 p. 56]
it becomes monoidal model
when restricted to 1-truncated classical base types,
So this is a well-behaved extension by symmetric monoidal chain complexes
of the original groupoid model for 1-truncated HoTT [Hofmann & Streicher 1994].
To get a sense of the nature of this extension,
focus on the “hearts” of these fiber-wise stable symmetric monoidal -categories, which form
-
over the point:
-
over any base homotopy type :
its category of flat vector bundles (“local systems”)
-
over varying discrete base spaces:
the category of indexed sets of complex vector spaces,
hence the free coproduct completion of :
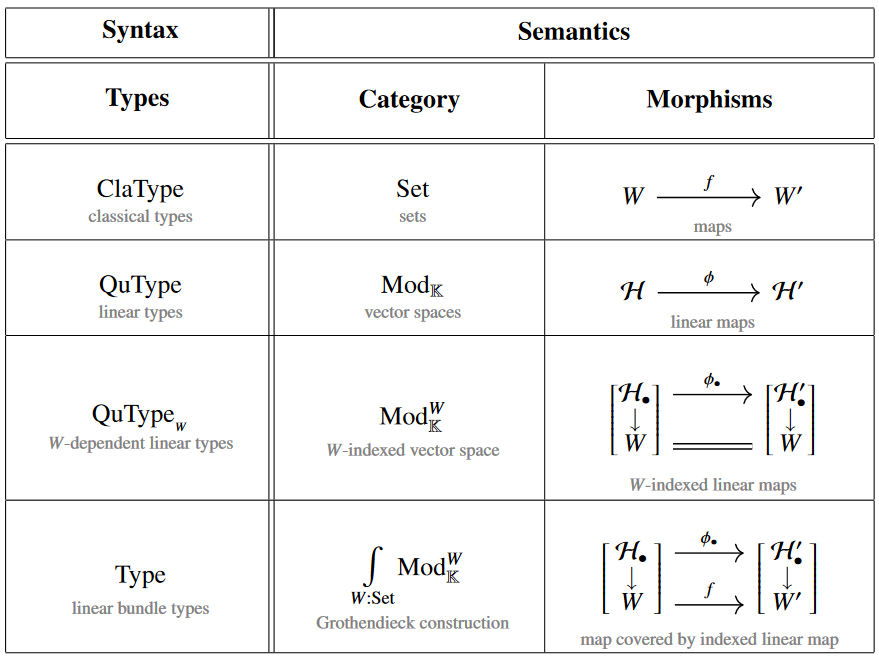
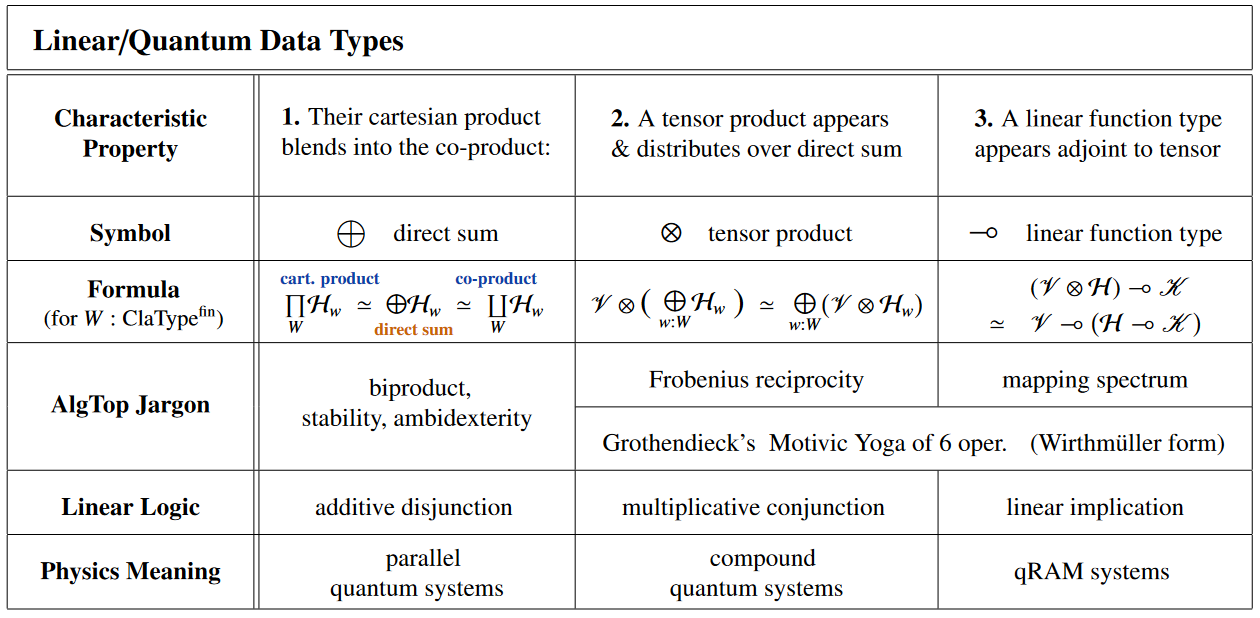
It is clear but maybe underappreciated [Pratt 1993; Valiron & Zdancewic 2014; cf. Sati and S. 2023b pp. 53]
that these categories happen to be models of
(the multiplicative fragment of) linear type theory:
Similarly clear but long underappreciated [Pratt 1992; Selinger & Valiron 2005; Abramsky & Duncan 2006]:
Where type theory is about computing,
linear type theory may be understood as being about quantum computation:
Accordingly, over sets (0-truncated objects), the above categories serve
as categorical semantics for quantum programming languages such as:
-
Proto-Quipper (cf. the talks by Lee and by Riley)
-
the ZX-calculus (cf. the talk by Rand)
-
and others (cf. the talk by Paykin)
I’ll expand on this further below:
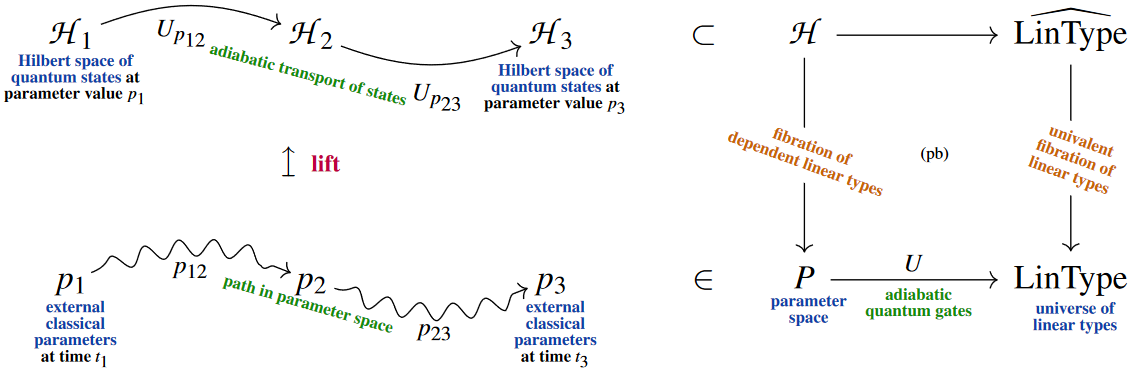
Moreover [Myers, Sati and S. 2024] (cf. the talk by Myers),
over homotopy 1-types, serves as
categorical semantics for topological quantum gates
Remarkably [Myers, Sati and S. 2024, Thm. 6.8]
here we have a correspondence between
This “quantum reflection” of -toposes goes even beyond quantum computation
to capture the “hardware” quantum physics of quantum systems:
E.g. when KU then in then
-
the intrinsic cohomology is twisted K-theory,
-
suitable base change-operations give fiber integration in twisted K-theory
which serves to describe
-
[cf. Nuiten 2013]
cohomologicalgeometric quantization
of finite-dimensional phase spaces (symplectic/Poisson manifolds),
-
[cf. Sati and S. 2023]
classification of topological phases of quantum materials
which serve as potential hardware for topological quantum computation.
Even this “works formally” [S. 2014 pp. 48, 53, 65]:
behaves like one would expect for
a categorical semantics of an extension of homotopy type theory by
some kind of dependent linear (stable) homotopy types.
This motivates to ask for a formalization of
Quantization via Linear Homotopy Types [arXiv:1402.7041]
and ask for an extension of HoTT by language features
whose categorical semantics single out tangent -toposes among all -toposes
which may serve as a natural quantum programming/certification.
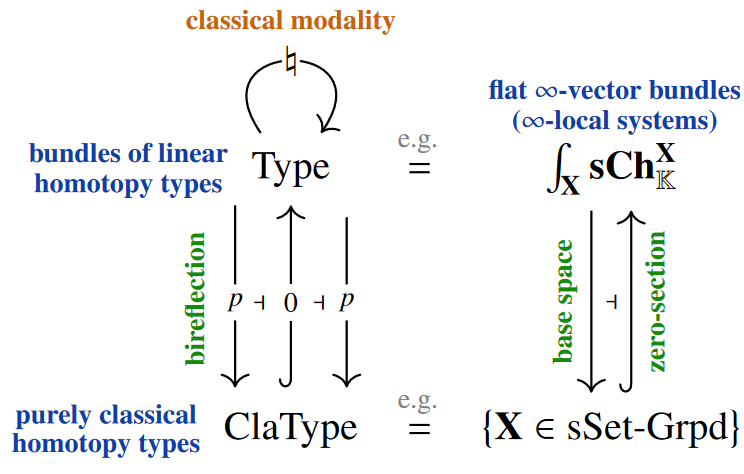
Concretely [S. 2013, Prop. 4.1.9, p. 446],
tangent -toposes are infinitesimally cohesive over their base topos .
Hence a would-be “Linear Homotopy Type Theory” should
first of all be a modal extension of HoTT
by an ambidextrous modality expressing the bireflective subcategory
into more general classical+quantum types
(Bohr‘s quantum/classical divide).
Such a classically-modal LHoTT was then
given by [Riley, Finster & Licata 2021] (cf. the talk by Finster) and
a syntax for the (“external”) tensor product was given by [Riley 2022] (see talk by Riley)
Getting to the bottom of how knows about the nature of quantum systems
one finds [Schreiber 2014; Sati and S. 2023a pp. 43; Sati and S. 2023b pp. 62]
that the base change adjoint triples on the system of dependent linear type universes
together with the linear tensor product and its internal hom
constitutes the Wirthmüller form of Grothendieck‘s yoga of six operations in motivic homotopy theory
— which for short we refer to as the Motivic Yoga.
Therefore a good quantum programming language should be
one that expresses and verifies the Motivic Yoga.
This is the case for LHoTT [Riley 2022, §2.4]
And hence we want to see how to go about formulating
with operational semantics in tangent -toposes
naturally embeddable into LHoTT.
(2) Modal Quantum Circuit Logic via Dependent Linear Types
The Quantum Monadology [Sati and S. 2023]
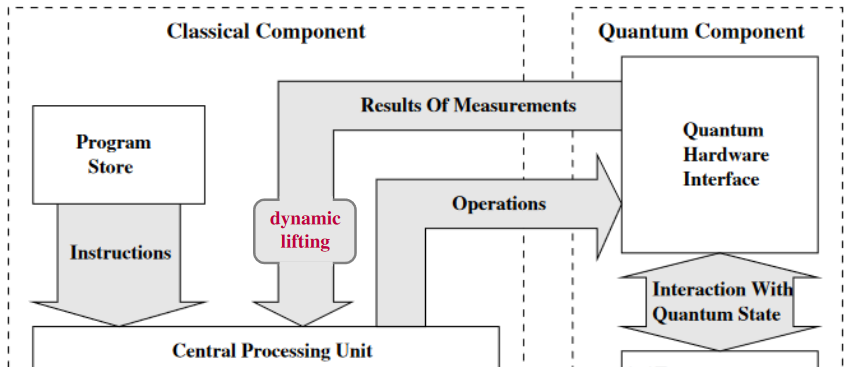
The theory of computational effects in functional programming languages suggests that
quantum effects such as
should have a formal reflection in terms of suitable
(co-)monads/modal operators on a linear data type system.
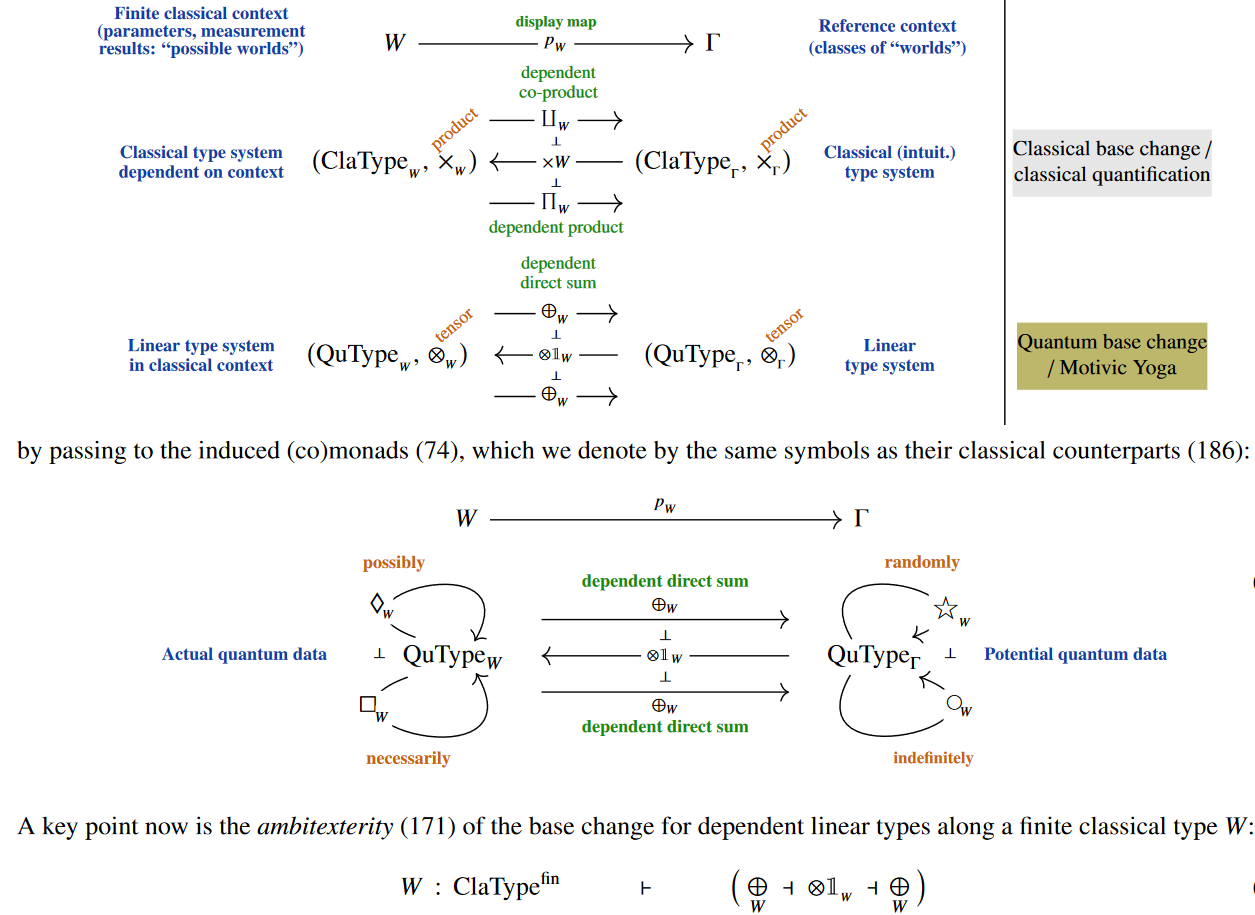
Our fundamental observation is that
in a dependent linear type theory which satisfies the Motivic Yoga (e.g. LHoTT)
suitale such (co-)monads are definable (i.e., by admissible inference rules)
induced from the base change adjoint triple restricted to dependent linear types:
dependent pair type context extension dependent product type
Remarkably [Sati and S. 2023b §2 pp. 53]
this automatically implements
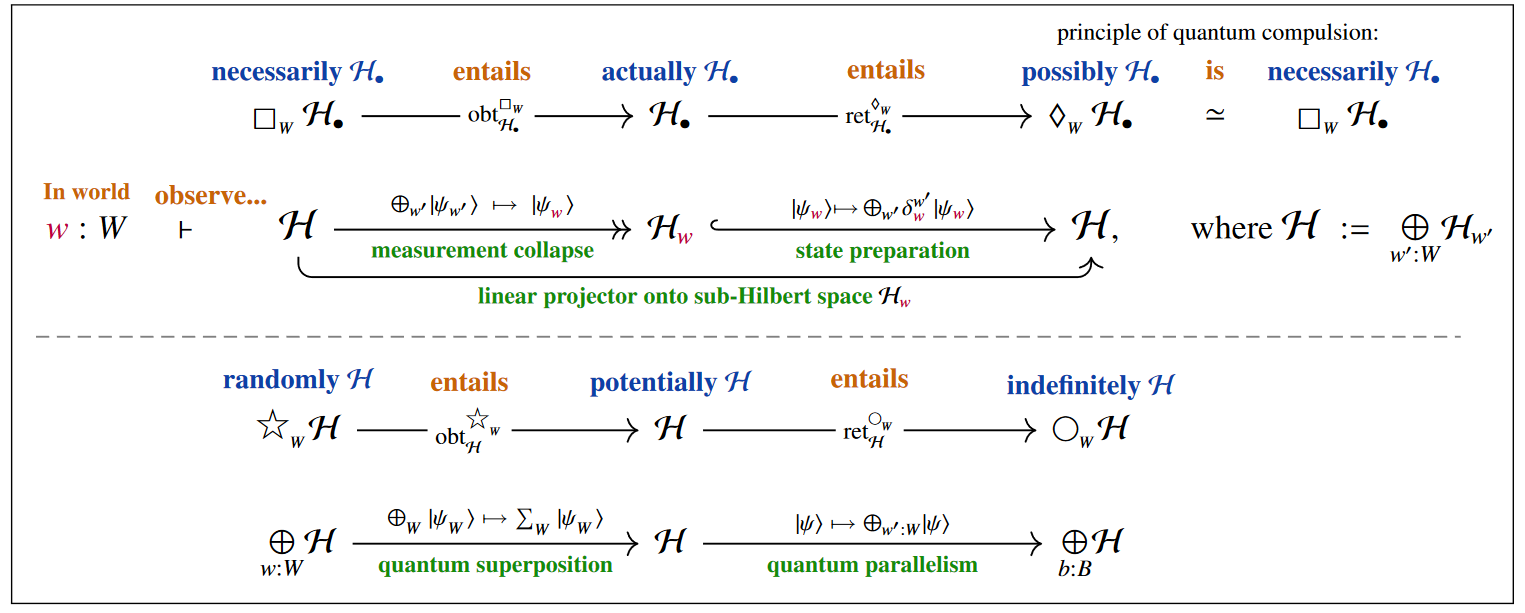
a quantum version of epistemic modal logic (S5)
which accurately reflects
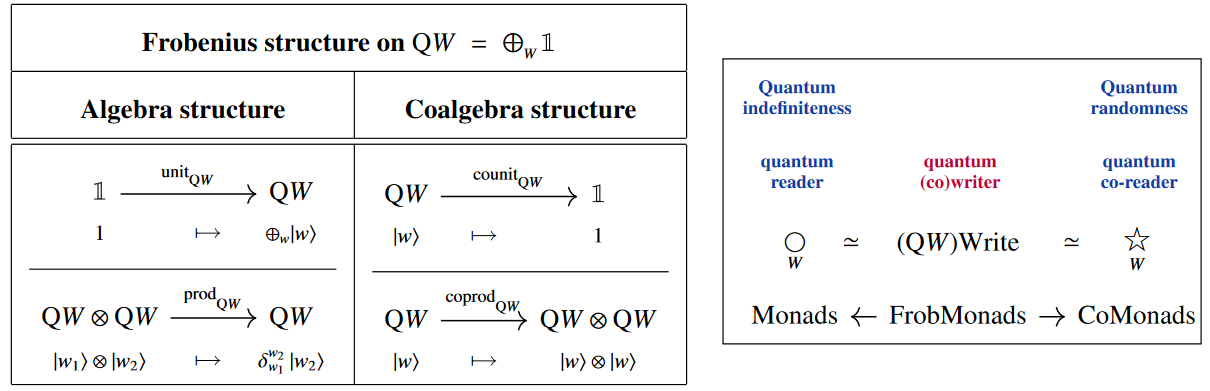
By ambidexterity/quantum compulsion one finds that [Prop. 2.34 p. 75]
the quantum indefiniteness/randomness modalities unify into a Frobenius monad:
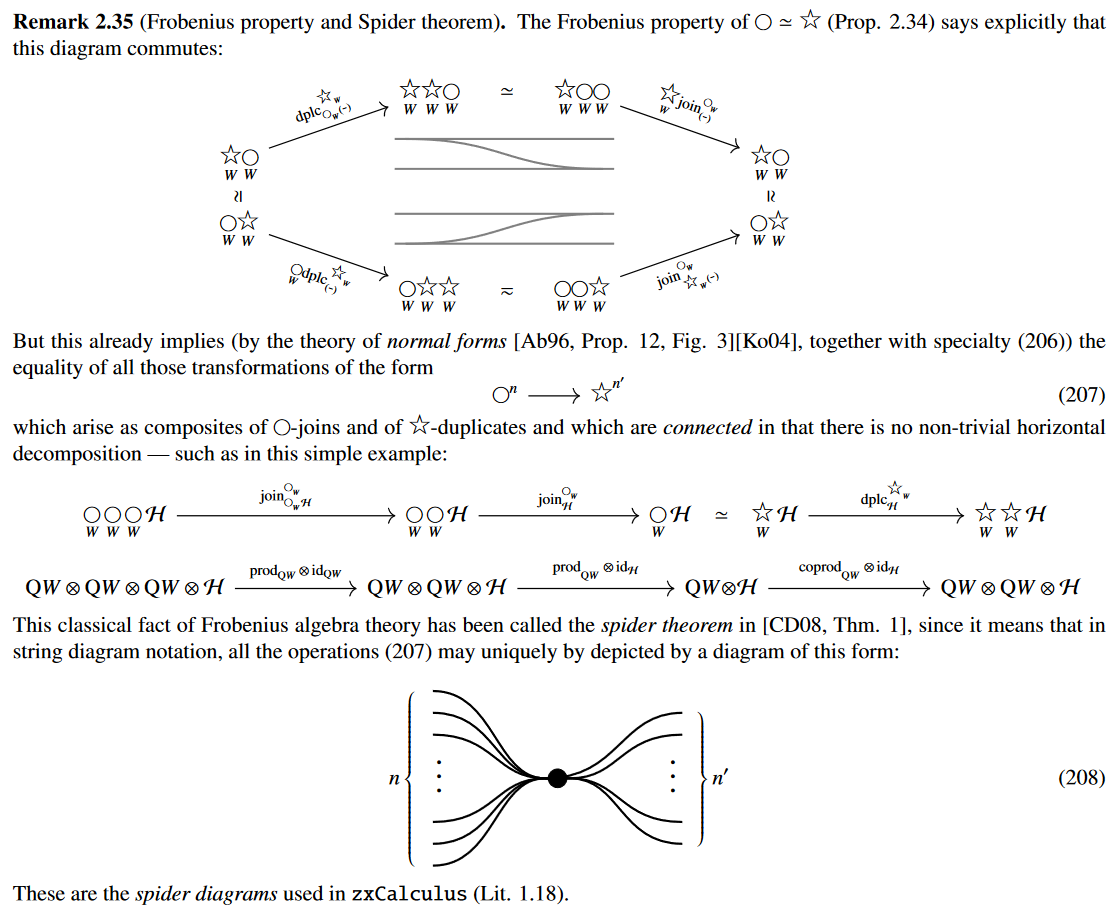
satisfying the Frobenius normal form/Spider theorem:
This recovers (and hence may serve to certify)
the typing of quantum measurement used in the ZX-calculus [Coecke and Pavlović 2008; Coecke and Duncan 2008]
(cf. the talk by Rand).
Next, it is noteworthy that
dependent linear types are monadic over plain linear types:
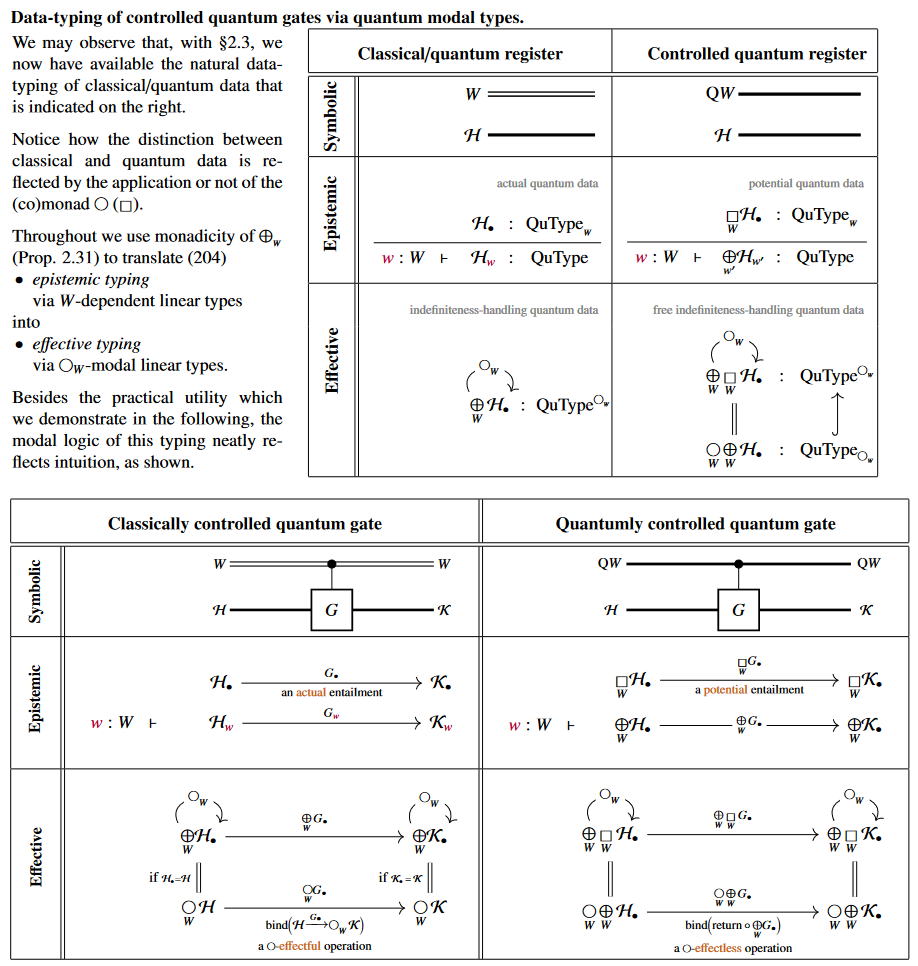
This provides the following
natural typings of quantum gates/quantum circuits ( quantum circuits via dependent linear types)
(1) typing of controlled quantum gates:
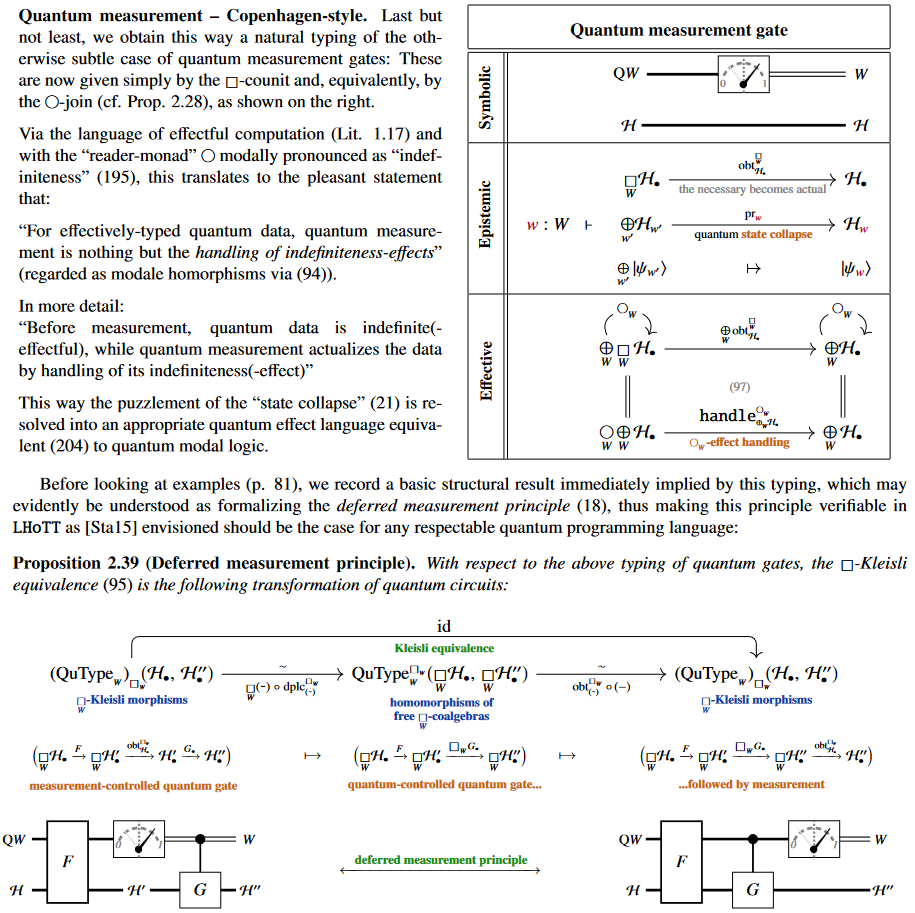
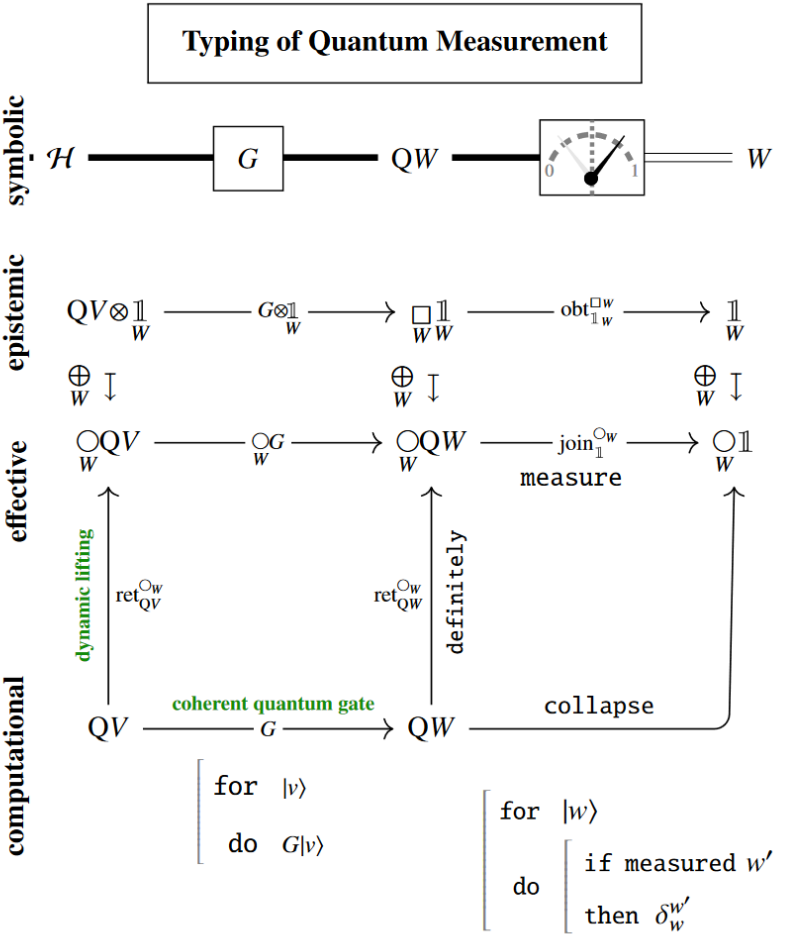
(2) typing of quantum measurement:
Hence the deferred measurement principle is verified in LHoTT as an instance of the Kleisli equivalence for the quantum necessity modality.
(3) typing of dynamic lifting by passage through the unit/return operation of the indefiniteness modality:
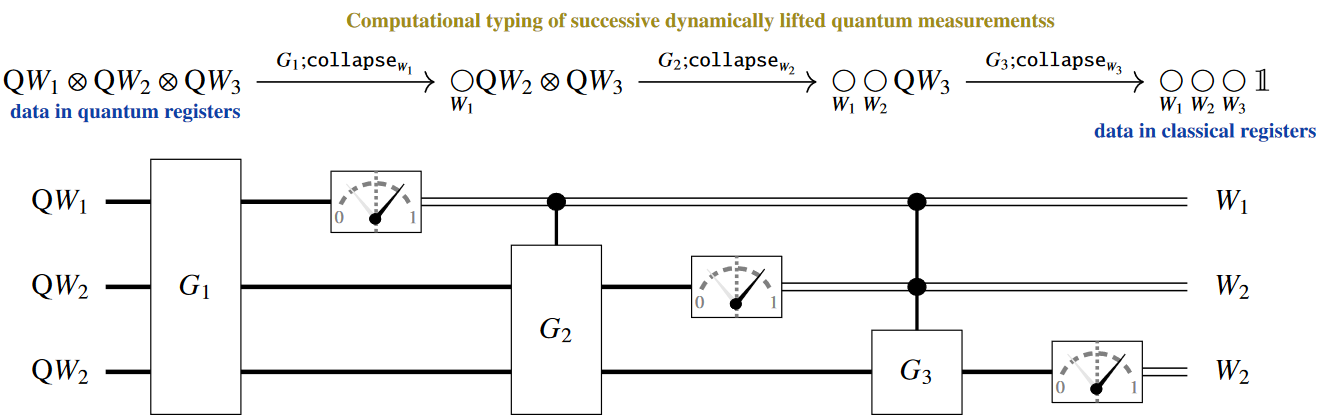
(4) typing of incremental quantum measurement:
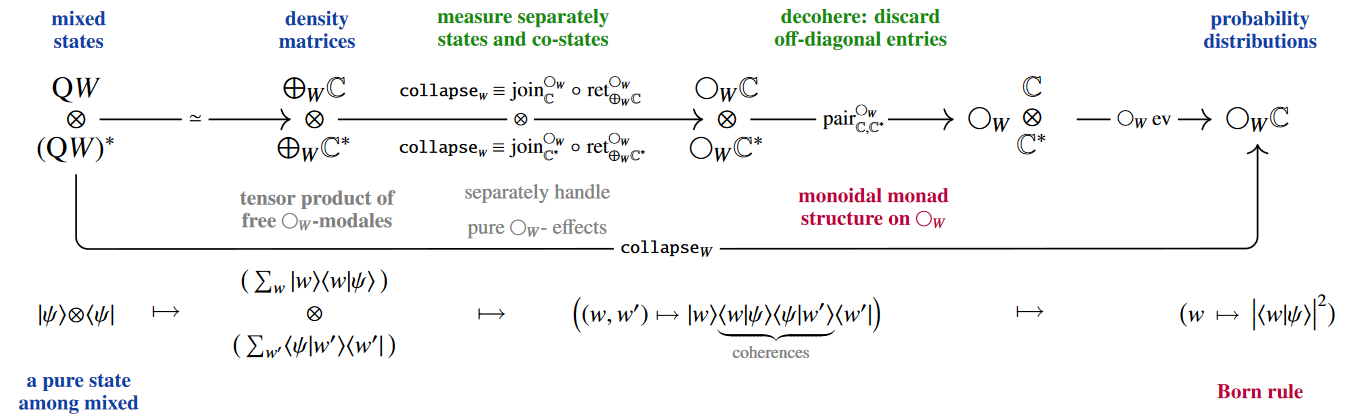
(5) typing of quantum measurement on mixed states and the Born rule
by monoidality of quantum indefiniteness [Prop. 2.36 p. 77]
In summary,
we find comprehensive expression
of quantum information/computing structures
in the internal language (LHoTT)
of tangent -toposes.
But in fact, up to this point we have
only used the 0-truncated/heart-sector of the linear homotopy type system.
The remaining higher types system turns out to reflect
fine-structure of topological quantum computation:
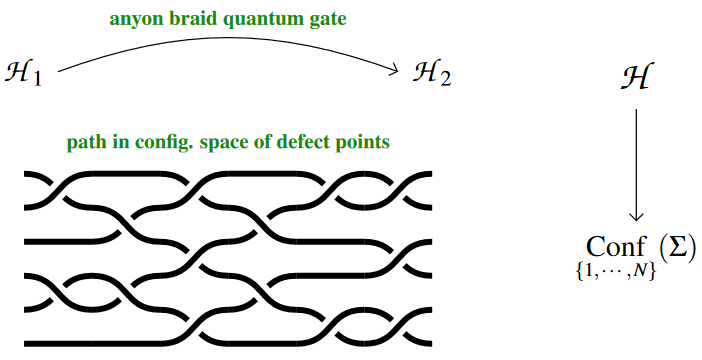
(3) Topological Quantum Gates via Linear Type Transport
Topological Quantum Gates in HoTT
(cf. following talk by Myers)
Related presentations:
-
Topological Quantum Programming in
TED-Ktalk at PlanQC 2022 33 (15 Sep 2022)
-
Quantum Data Types via Linear Homotopy Type Theory
talk at Workshop on Quantum Software @ QTML 2022, Naples, 12 Nov 2022
[slides: pdf]
-
Effective Quantum Certification via Linear Homotopy Types,
talk at Colloquium of the Topos Institute
Part I: 13 April 2023 [video: YT, slides:pdf]
Part II: 24 Aug 2023 [video:YT, slides:pdf]
-
Topological Quantum Programming via Linear Homotopy Types
talk at: Homotopy Type Theory Electronic Seminar (01 Feb 2024)
Last revised on April 27, 2024 at 07:27:21. See the history of this page for a list of all contributions to it.