nLab topological quantum computation
Context
Constructivism, Realizability, Computability
constructive mathematics, realizability, computability
propositions as types, proofs as programs, computational trinitarianism
Constructive mathematics
Realizability
Computability
Topological physics
Topological Physics – Phenomena in physics controlled by the topology (often: the homotopy theory) of the physical system.
General theory:
In metamaterials:
-
topological phononics (sound waves?)
For quantum computation:
Contents
Idea
In topological quantum computation one aims to make use of quantum systems described by topological quantum field theory for quantum computation, the idea being that the defining invariance of TQFTs under small deformations implements an intrinsic fault tolerance of the quantum computer against noise and decoherence (see also at quantum error correction).
On Anyons in 2+1 d
The standard paradigm for potentially realizing topological quantum computation in practice (Kitaev 03, Freedman, Kitaev, Larsen & Wang03) considers adiabatic braiding of defect anyons in effectively 2-dimensional quantum materials, such as in the quantum Hall effect and effectively described by some kind of Chern-Simons theory/Reshetikhin-Turaev theory:
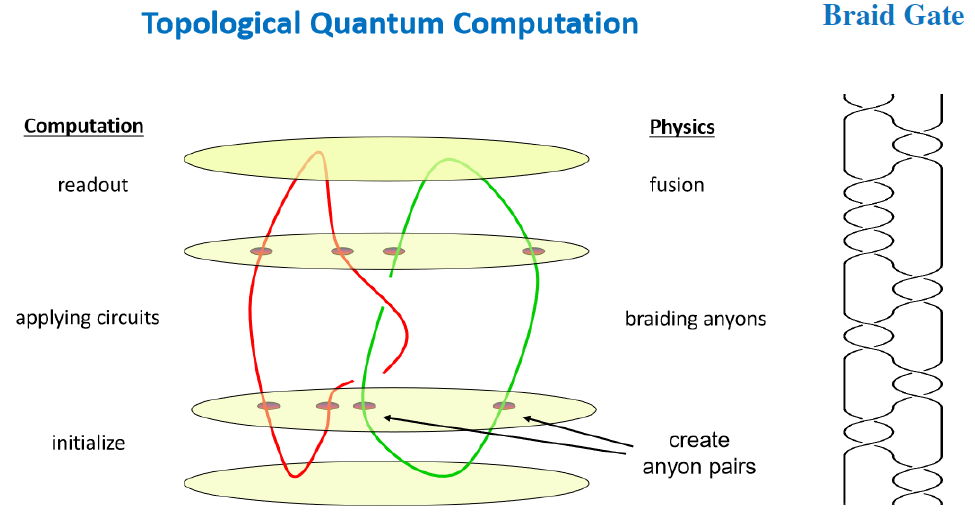
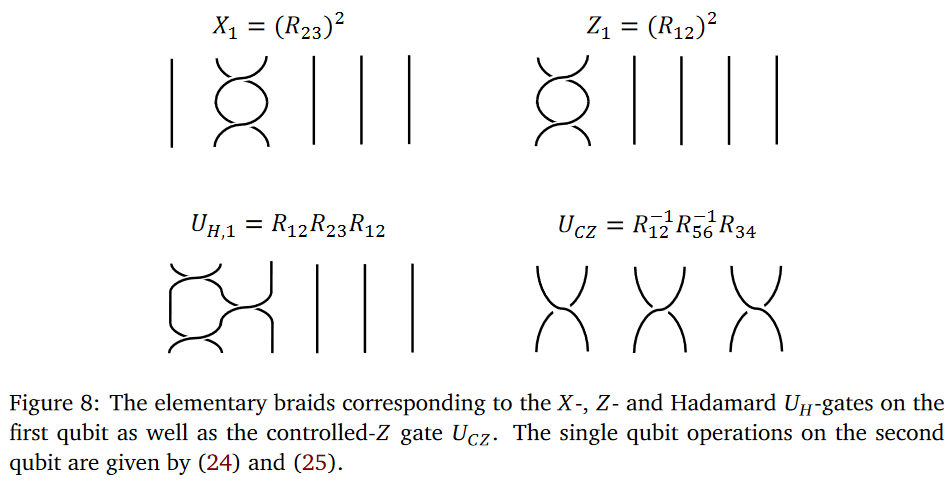
Here topological quantum gates are encoded by braid group-elements and are executed by actions through braid representations on the space of quantum states:

Extended TQC?
It is interesting to note that:
-
(pure) braid group representations are equivalently degree-1 cocycles in the non-abelian cohomology of the configuration space of points (ordered) in the Euclidean plane,;
-
as such, braid representations are the first stage in a sequence that continues with weight systems on horizontal chord diagrams, these being the complex cohomology in higher degree of the configuration space of points (ordered) in Euclideam 3-space (see at weight systems are cohomology of loop space of configuration space):
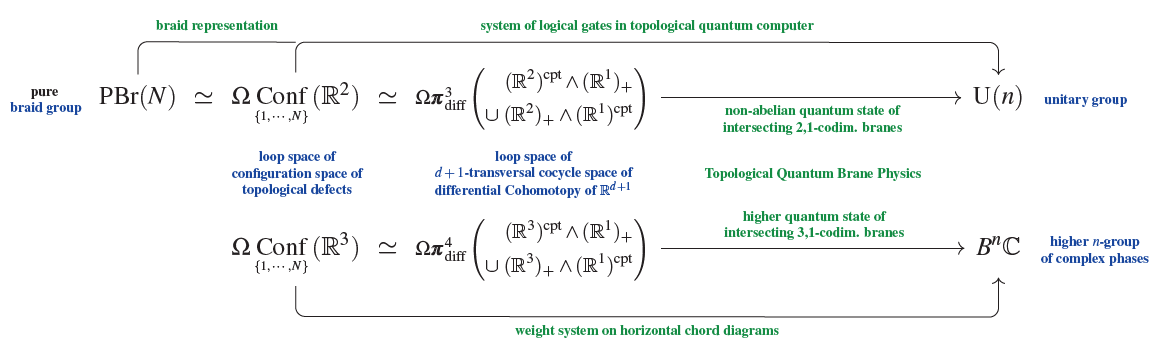
Here
-
is an Eilenberg-MacLane space/classifying space for the pure braid group
-
is a simply connected higher homotopy type:
This means that while every individual loop in is homotopically trivial (all “braid-gates” are equivalent) there is now non-trivial structure in higher-dimensional deformation families of braids (which is absent in ). Such structure would be reflected by extended TQFT.
Related concepts
References
Need for topological protection
Highlighting the need for topological stabilization mechanisms:
-
Jay Sau, A Roadmap for a Scalable Topological Quantum Computer, Physics 10 68 (2017)
“small machines are unlikely to uncover truly macroscopic quantum phenomena, which have no classical analogs. This will likely require a scalable approach to quantum computation. […] based on […] topological quantum computation (TQC) as envisioned by Alexei Kitaev and Michael Freedman […] The central idea of TQC is to encode qubits into states of topological phases of matter. Qubits encoded in such states are expected to be topologically protected, or robust, against the ‘prying eyes’ of the environment, which are believed to be the bane of conventional quantum computation.”
-
Sankar Das Sarma, Quantum computing has a hype problem, MIT Technology Review (March 2022)
“The qubit systems we have today are a tremendous scientific achievement, but they take us no closer to having a quantum computer that can solve a problem that anybody cares about. What is missing is the breakthrough bypassing quantum error correction by using far-more-stable qubits, in an approach called topological quantum computing.”
Topological quantum computation with anyons
The idea of topological quantum computation via a Chern-Simons theory with anyon braiding defects is due to:
-
Alexei Kitaev, Fault-tolerant quantum computation by anyons, Annals Phys. 303 (2003) 2-30 arXiv:quant-ph/9707021, doi:10.1016/S0003-4916(02)00018-0
-
Michael Freedman, P/NP, and the quantum field computer, Proc. Nat. Acad. Sci. 95 1 (1998) 98-101 doi:10.1073/pnas.95.1.9
-
Michael Freedman, Alexei Kitaev, Michael Larsen, Zhenghan Wang, Topological quantum computation, Bull. Amer. Math. Soc. 40 (2003), 31-38 (arXiv:quant-ph/0101025, doi:10.1090/S0273-0979-02-00964-3, pdf)
-
Michael Freedman, Michael Larsen, Zhenghan Wang, A modular functor which is universal for quantum computation, Communications in Mathematical Physics. 227 3 (2002) 605-622 arXiv:quant-ph/0001108, doi:10.1007/s002200200645
(specifically via su(2)-anyons)
-
Chetan Nayak, Steven H. Simon, Ady Stern, Michael Freedman, Sankar Das Sarma, Non-Abelian Anyons and Topological Quantum Computation, Rev. Mod. Phys. 80 1083 (2008) arXiv:0707.1888, doi:10.1103/RevModPhys.80.1083
-
Dmitry Melnikov, Andrei Mironov, Sergey Mironov, Alexei Morozov, Andrey Morozov, Towards topological quantum computer, Nucl. Phys. B926 (2018) 491-508 (arXiv:1703.00431, doi:10.1016/j.nuclphysb.2017.11.016)
and via a Dijkgraaf-Witten theory (like Chern-Simons theory but with discrete gauge group):
-
R. Walter Ogburn, John Preskill, Topological Quantum Computation, in: Quantum Computing and Quantum Communications, Lecture Notes in Computer Science 1509, Springer (1998) doi:10.1007/3-540-49208-9_31
-
Carlos Mochon, Anyons from non-solvable finite groups are sufficient for universal quantum computation, Phys. Rev. A 67 022315 (2003) arXiv:quant-ph/0206128, doi:10.1103/PhysRevA.67.022315
-
Carlos Mochon, Anyon computers with smaller groups, Phys. Rev. A 69 032306 (2004) arXiv:quant-ph/0306063, doi:10.1103/PhysRevA.69.032306
Textbook accounts:
-
Zhenghan Wang, Topological Quantum Computation, CBMS Regional Conference Series in Mathematics 112, AMS 2010 (ISBN-13: 978-0-8218-4930-9, pdf)
-
Jiannis K. Pachos, Introduction to Topological Quantum Computation, Cambridge University Press (2012) doi:10.1017/CBO9780511792908
-
Tudor D. Stanescu, Part IV of: Introduction to Topological Quantum Matter & Quantum Computation, CRC Press 2020 (ISBN:9780367574116)
-
Steven H. Simon, Topological Quantum, 2021 pdf, webpage
Review:
-
Louis Kauffman, Quantum Topology and Quantum Computing, in: Samuel J. Lomonaco (ed.), Quantum Computation: A Grand Mathematical Challenge for the Twenty-First Century and the Millennium, Proceedings of Symposia in Applied Mathematics 58, AMS (2002) [pdf, doi:10.1090/psapm/058]
(in relation to quantum topology)
-
Gavin K. Brennen, Jiannis K. Pachos, Why should anyone care about computing with anyons?, Proc. R. Soc. A 464 (2008) 1-24 arXiv:0704.2241, doi:10.1098/rspa.2007.0026
-
Ady Stern, Netanel H. Lindner, Topological Quantum Computation – From Basic Concepts to First Experiments, Science 339 6124 (2013) 1179-1184 (doi:10.1126/science.1231473)
-
Eric C. Rowell, An Invitation to the Mathematics of Topological Quantum Computation, J. Phys.: Conf. Ser. 698 (2016) 012012 (doi:10.1088/1742-6596/698/1/012012)
-
Ananda Roy, David P. DiVincenzo, Topological Quantum Computing, Lecture notes of the 48th IFF Spring School (2017) arXiv:1701.05052
-
Ville Lahtinen, Jiannis K. Pachos, A Short Introduction to Topological Quantum Computation, SciPost Phys. 3 021 (2017) arXiv:1705.04103, doi:10.21468/SciPostPhys.3.3.021
-
Eric C. Rowell, Zhenghan Wang, Mathematics of Topological Quantum Computing, Bull. Amer. Math. Soc. 55 (2018), 183-238 (arXiv:1705.06206, doi:10.1090/bull/1605)
-
Bernard Field, Tapio Simula, Introduction to topological quantum computation with non-Abelian anyons, Quantum Science and Technology 3 (2018) 045004 arXiv:1802.06176, doi:10.1088/2058-9565/aacad2
-
Muhammad Ilyas, Quantum Field Theories, Topological Materials, and Topological Quantum Computing arXiv:2208.09707
-
Eric C. Rowell, Braids, Motions and Topological Quantum Computing arXiv:2208.11762
Focus on abelian anyons:
-
Jiannis K. Pachos, Quantum computation with abelian anyons on the honeycomb lattice, International Journal of Quantum Information 4 6 (2006) 947-954 (arXiv:quant-ph/0511273)
-
James Robin Wootton, Dissecting Topological Quantum Computation, 2010 (pdf, pdf)
“non-Abelian anyons are usually assumed to be better suited to the task. Here we challenge this view, demonstrating that Abelian anyon models have as much potential as some simple non-Abelian models.”
-
Wade Bloomquist, Zhenghan Wang, On Topological Quantum Computing With Mapping Class Group Representations, J. Phys. A: Math. Theor. 52 (2019) 015301 (arXiv:1805.04622, doi:10.1088/1751-8121/aaeea1)
-
Seth Lloyd, Quantum computation with abelian anyons, Quantum Information Processing 1 1/2 (2002) (arXiv:quant-ph/0004010, doi:10.1023/A:1019649101654)
Realization in experiment:
-
Daniel Nigg, Markus Mueller, Esteban A. Martinez, Philipp Schindler, Markus Hennrich, Thomas Monz, Miguel A. Martin-Delgado, Rainer Blatt,
Experimental Quantum Computations on a Topologically Encoded Qubit, Science 18 Jul 2014: Vol. 345, Issue 6194, pp. 302-305 (arXiv:1403.5426, doi:10.1126/science.1253742)
(for quantum error correction)
Simulation of Ising anyons in a lattice of ordinary superconducting qbits:
- T. Andersen et al. Observation of non-Abelian exchange statistics on a superconducting processor arXiv:2210.10255
Braid group representations (as topological quantum gates)
On linear representations of braid groups (see also at braid group statistics and interpretation as quantum gates in topological quantum computation):
- Ivan Marin, On the representation theory of braid groups, Annales mathématiques Blaise Pascal, 20 2 (2013) 193-260 (arXiv:math/0502118, dml:275607)
Review:
-
Chen Ning Yang, M. L. Ge (eds.). Braid Group, Knot Theory and Statistical Mechanics, Advanced Series in Mathematical Physics 9, World Scientific (1991) doi:10.1142/0796
(focus on quantum Yang-Baxter equation)
-
Camilo Arias Abad, Introduction to representations of braid groups, Rev. colomb. mat. vol.49 no.1 (2015) (arXiv:1404.0724, doi:10.15446/recolma.v49n1.54160)
-
Toshitake Kohno, Introduction to representation theory of braid groups, Peking 2018 (pdf, pdf)
in relation to modular tensor categories:
- Colleen Delaney, Lecture notes on modular tensor categories and braid group representations, 2019 (pdf, pdf)
Braid representations from the monodromy of the Knizhnik-Zamolodchikov connection on bundles of conformal blocks over configuration spaces of points:
-
Ivan Todorov, Ludmil Hadjiivanov, Monodromy Representations of the Braid Group, Phys. Atom. Nucl. 64 (2001) 2059-2068; Yad.Fiz. 64 (2001) 2149-2158 arXiv:hep-th/0012099, doi:10.1134/1.1432899
-
Ivan Marin, Sur les représentations de Krammer génériques, Annales de l’Institut Fourier, 57 6 (2007) 1883-1925 numdam:AIF_2007__57_6_1883_0
and understood in terms of anyon statistics:
- Xia Gu, Babak Haghighat, Yihua Liu, Ising- and Fibonacci-Anyons from KZ-equations, J. High Energ. Phys. 2022 15 (2022) [doi:10.1007/JHEP09(2022)015, arXiv:2112.07195]
Braid representations seen inside the topological K-theory of the braid group‘s classifying space:
-
Alejandro Adem, Daniel C. Cohen, Frederick R. Cohen, On representations and K-theory of the braid groups, Math. Ann. 326 (2003) 515-542 (arXiv:math/0110138, doi:10.1007/s00208-003-0435-8)
-
Frederick R. Cohen, Section 3 of: On braid groups, homotopy groups, and modular forms, in: J.M. Bryden (ed.), Advances in Topological Quantum Field Theory, Kluwer 2004, 275–288 (pdf)
See also:
- R. B. Zhang, Braid group representations arising from quantum supergroups with arbitrary and link polynomials, Journal of Mathematical Physics 33, 3918 (1992) (doi:10.1063/1.529840)
As quantum gates for topological quantum computation with anyons:
-
Louis H. Kauffman, Samuel J. Lomonaco, Braiding Operators are Universal Quantum Gates, New Journal of Physics, Volume 6, January 2004 (arXiv:quant-ph/0401090, doi:10.1088/1367-2630/6/1/134)
-
Samuel J. Lomonaco, Louis Kauffman, Topological Quantum Computing and the Jones Polynomial, Proc. SPIE 6244, Quantum Information and Computation IV, 62440Z (2006) (arXiv:quant-ph/0605004)
(braid group representation serving as a topological quantum gate to compute the Jones polynomial)
-
Louis H. Kauffman, Samuel J. Lomonaco, Topological quantum computing and braid group representations, Proceedings Volume 6976, Quantum Information and Computation VI; 69760M (2008) (doi:10.1117/12.778068, rg:228451452)
-
C.-L. Ho, A.I. Solomon, C.-H.Oh, Quantum entanglement, unitary braid representation and Temperley-Lieb algebra, EPL 92 (2010) 30002 (arXiv:1011.6229)
-
Louis H. Kauffman, Majorana Fermions and Representations of the Braid Group, International Journal of Modern Physics AVol. 33, No. 23, 1830023 (2018) (arXiv:1710.04650, doi:10.1142/S0217751X18300235)
-
David Lovitz, Universal Braiding Quantum Gates [arXiv:2304.00710]
Introduction and review:
-
Colleen Delaney, Eric C. Rowell, Zhenghan Wang, Local unitary representations of the braid group and their applications to quantum computing, Revista Colombiana de Matemáticas(2017), 50 (2):211 (arXiv:1604.06429, doi:10.15446/recolma.v50n2.62211)
-
Eric C. Rowell, Braids, Motions and Topological Quantum Computing arXiv:2208.11762
Realization of Fibonacci anyons on quasicrystal-states:
- Marcelo Amaral, David Chester, Fang Fang, Klee Irwin, Exploiting Anyonic Behavior of Quasicrystals for Topological Quantum Computing, Symmetry 14 9 (2022) 1780 arXiv:2207.08928, doi:10.3390/sym14091780
Realization on supersymmetric spin chains:
- Indrajit Jana, Filippo Montorsi, Pramod Padmanabhan, Diego Trancanelli, Topological Quantum Computation on Supersymmetric Spin Chains arXiv:2209.03822
See also:
- Yuanjie Ren, Peter Shor, Topological quantum computation assisted by phase transitions [arXiv:2311.00103]
Compilation to braid gate circuits
On approximating (cf. the Solovay-Kitaev theorem) given quantum gates by (i.e. compiling them to) cicuits of anyon braid gates (generally considered for su(2)-anyons and here mostly for universal Fibonacci anyons, to some extent also for non-universal Majorana anyons):
-
Nicholas E. Bonesteel, Layla Hormozi, Georgios Zikos, Steven H. Simon, Braid Topologies for Quantum Computation, Phys. Rev. Lett. 95 140503 (2005) arXiv:quant-ph/0505065, doi:10.1103/PhysRevLett.95.140503
-
Layla Hormozi, Georgios Zikos, Nicholas E. Bonesteel, Steven H. Simon, Topological Quantum Compiling, Phys. Rev. B 75 165310 (2007) arXiv:quant-ph/0610111, doi:10.1103/PhysRevB.75.165310
-
Layla Hormozi, Nicholas E. Bonesteel, Steven H. Simon, Topological Quantum Computing with Read-Rezayi States, Phys. Rev. Lett. 103 160501 (2009) doi:10.1103/PhysRevLett.103.160501, arXiv:0903.2239
-
M. Baraban, Nicholas E. Bonesteel, Steven H. Simon, Resources required for topological quantum factoring, Phys. Rev. A 81 062317 (2010) doi:10.1103/PhysRevA.81.062317, arXiv:1002.0537
(focus on compiling Shor's algorithm)
-
Vadym Kliuchnikov, Alex Bocharov, Krysta M. Svore, Asymptotically Optimal Topological Quantum Compiling, Phys. Rev. Lett. 112 140504 (2014) arXiv:1310.4150, journal: doi:10.1103/PhysRevLett.112.140504, talk recording: doi:10.48660/13100129
-
Joren W. Brunekreef, Topological Quantum Computation and Quantum Compilation, Utrecht (2014) studenttheses.uu.nl:20.500.12932/17738
-
Yuan-Hang Zhang, Pei-Lin Zheng, Yi Zhang, Dong-Ling Deng, Topological Quantum Compiling with Reinforcement Learning, Phys. Rev. Lett. 125 170501 (2020) doi:2004.04743, doi:10.1103/PhysRevLett.125.170501
-
Emil Génetay-Johansen, Tapio Simula, Section IV of: Fibonacci anyons versus Majorana fermions – A Monte Carlo Approach to the Compilation of Braid Circuits in Anyon Models, PRX Quantum 2 010334 (2021) arXiv:2008.10790, doi:10.1103/PRXQuantum.2.010334
-
Cheng-Qian Xu, D. L. Zhou, Quantum teleportation using Ising anyons, Phys. Rev. A 106 012413 (2022) arXiv:2201.11923, doi:10.1103/PhysRevA.106.012413
(focus on implemening the quantum teleportation-protocol with Ising anyons)
Approximating all topological quantum gates by just the weaves among all braids:
-
Steven H. Simon, Nick E. Bonesteel, Michael H. Freedman, N. Petrovic, Layla Hormozi, Topological Quantum Computing with Only One Mobile Quasiparticle, Phys. Rev. Lett. 96 (2006) 070503 (arXiv:quant-ph/0509175, doi:10.1103/PhysRevLett.96.070503)
-
Layla Hormozi, Georgios Zikos, Nick E. Bonesteel, Steven H. Simon, Topological quantum compiling, Phys. Rev. B 75, 165310 (doi:10.1103/PhysRevB.75.165310, arXiv:quant-ph/0610111)
-
Mohamed Taha Rouabah, Compiling single-qubit braiding gate for Fibonacci anyons topological quantum computation (arXiv:2008.03542)
Anyons in the quantum Hall liquids
References on anyon-excitations (satisfying braid group statistics) in the quantum Hall effect (for more on the application to topological quantum computation see the references there):
The prediction of abelian anyon-excitations in the quantum Hall effect (i.e. satisfying braid group statistics in 1-dimensional linear representations of the braid group):
-
B. I. Halperin, Statistics of Quasiparticles and the Hierarchy of Fractional Quantized Hall States, Phys. Rev. Lett. 52, 1583 (1984) (doi:10.1103/PhysRevLett.52.1583)
Erratum Phys. Rev. Lett. 52, 2390 (1984) (doi:10.1103/PhysRevLett.52.2390.4)
-
Daniel Arovas, J. R. Schrieffer, Frank Wilczek, Fractional Statistics and the Quantum Hall Effect, Phys. Rev. Lett. 53, 722 (1984) doi:10.1103/PhysRevLett.53.722
The original discussion of non-abelian anyon-excitations in the quantum Hall effect (i.e. satisfying braid group statistics in higher dimensional linear representations of the braid group, related to modular tensor categories):
- Gregory Moore, Nicholas Read, Nonabelions in the fractional quantum Hall effect, Nucl. Phys. 360B(1991)362 (pdf, doi:10.1016/0550-3213(91)90407-O)
Review:
- Ady Stern, Anyons and the quantum Hall effect – A pedagogical review, Annals of Physics Volume 323, Issue 1, January 2008, Pages 204-249 (doi:10.1016/j.aop.2007.10.008, arXiv:0711.4697)
Anyons in topological superconductors
On anyon-excitations in topological superconductors.
via Majorana zero modes:
Original proposal:
- Nicholas Read, Dmitry Green, Paired states of fermions in two dimensions with breaking of parity and time-reversal symmetries, and the fractional quantum Hall effect, Phys. Rev. B61:10267, 2000 (arXiv:cond-mat/9906453)
Review:
-
Sankar Das Sarma, Michael Freedman, Chetan Nayak, Majorana Zero Modes and Topological Quantum Computation, npj Quantum Information 1, 15001 (2015) (nature:npjqi20151)
-
Nur R. Ayukaryana, Mohammad H. Fauzi, Eddwi H. Hasdeo, The quest and hope of Majorana zero modes in topological superconductor for fault-tolerant quantum computing: an introductory overview (arXiv:2009.07764)
-
Yusuke Masaki, Takeshi Mizushima, Muneto Nitta, Non-Abelian Anyons and Non-Abelian Vortices in Topological Superconductors [arXiv:2301.11614]
Further developments:
-
Meng Cheng, Victor Galitski, Sankar Das Sarma, Non-adiabatic Effects in the Braiding of Non-Abelian Anyons in Topological Superconductors, Phys. Rev. B 84, 104529 (2011) (arXiv:1106.2549)
-
Javad Shabani et al., Two-dimensional epitaxial superconductor-semiconductor heterostructures: A platform for topological superconducting networks, Phys. Rev. B 93 155402 (2016) [doi:10.1103/PhysRevB.93.155402, arXiv:1511.01127]
-
Javad Shabani et al., Zero-Energy Modes from Coalescing Andreev States in a Two-Dimensional Semiconductor-Superconductor Hybrid Platform, Phys. Rev. Lett. 119 (2017) 176805 [doi:10.1103/PhysRevLett.119.176805, arXiv:1703.03699]
-
Javad Shabani et al., Fusion of Majorana Bound States with Mini-Gate Control in Two-Dimensional Systems, Nature Communications 13 (2022) 1738-1747 [doi:10.1038/s41467-022-29463-6, arXiv:2101.09272]
-
Javad Shabani et al., Quasiparticle dynamics in epitaxial Al-InAs planar Josephson junctions, PRX Quantum 4 030339 (2023) [doi:10.1103/PRXQuantum.4.030339, arXiv:2303.04784]
via Majorana zero modes restricted to edges of topological insulators:
- Biao Lian, Xiao-Qi Sun, Abolhassan Vaezi, Xiao-Liang Qi, and Shou-Cheng Zhang, Topological quantum computation based on chiral Majorana fermions, PNAS October 23, 2018 115 (43) 10938-10942; first published October 8, 2018 (doi:10.1073/pnas.1810003115)
See also:
- Yusuke Masaki, Takeshi Mizushima, Muneto Nitta, Non-Abelian Anyons and Non-Abelian Vortices in Topological Superconductors arXiv:2301.11614
Last revised on March 7, 2023 at 13:03:10. See the history of this page for a list of all contributions to it.