nLab quaternion group
Context
Group Theory
- group, ∞-group
- group object, group object in an (∞,1)-category
- abelian group, spectrum
- super abelian group
- group action, ∞-action
- representation, ∞-representation
- progroup
- homogeneous space
Classical groups
Finite groups
Group schemes
Topological groups
Lie groups
Super-Lie groups
Higher groups
Cohomology and Extensions
Related concepts
Contents
Idea
The quaternion group of order 8, , is the finite subgroup of SU(2) of unit quaternions which consists of the canonical four basis-quaternions and their negatives:

This is isomorphic to the binary dihedral group of the same order . As such, the Dynkin diagram that corresponds to under the ADE-classification of finite subgroups of SU(2) is D4, the triality-invariant one.
graphics grabbed from Wikipedia here
This order-8 quaternion group is the first in a row of generalized quaternion groups, , which are also examples of dicyclic groups, which class forms part of an even larger family. We will treat both general dicyclic groups and the specific example of the quaternion group together.
Definitions
The dicyclic of order , , is the group defined by the presentation .
The quaternion group (of order 8) is then for .
The generalised quaternion group of order is with .
Properties
General
-
is (isomorphic to) a finite subgroup of as can be seen by taking generators and . For this simply yields the subgroup generated by and .
-
has another presentation as . as a power of each of the generators is central and , where is the dihedral group of order .
-
is a Hamiltonian group i.e. a non-abelian group such that every subgroup is normal. Moreover, a general structure theorem for Hamiltonian groups by Baer (1933) says that every Hamiltonian group has a direct product group-decomposition containing as a factor hence, in particular, every Hamiltonian group contains as a subgroup! (cf. Scott (1987, p.253))
-
is the multiplicative part of the quaternionic near-field . (cf. Weibel (2007))
Proposition
(inclusion of into finite subgroups of SU(2))
Among the finite subgroups of SU(2) (hence among all “finite quaternion groups”) the quaternion group of order 8, is a proper subgroup precisely of the three exceptional cases:
-
the binary tetrahedral group (normal),
-
the binary icosahedral group (not normal)
(e.g. Koca-Moc-Koca 16, p. 8, pointing to Coxeter-Moser 65 and Coxeter 73)
Character table
linear representation theory of binary dihedral group
dicyclic group quaternion group
| conjugacy classes: | 1 | 2 | 4A | 4B | 4C |
|---|---|---|---|---|---|
| their cardinality: | 1 | 1 | 2 | 2 | 2 |
| splitting field | with |
| field generated by characters |
character table over splitting field /complex numbers
| irrep | 1 | 2 | 4A | 4B | 4C | Schur index |
|---|---|---|---|---|---|---|
| 1 | 1 | 1 | 1 | 1 | 1 | |
| 1 | 1 | -1 | 1 | -1 | 1 | |
| 1 | 1 | 1 | -1 | -1 | 1 | |
| 1 | 1 | -1 | -1 | 1 | 1 | |
| 2 | -2 | 0 | 0 | 0 | 2 |
character table over rational numbers /real numbers
| irrep | 1 | 2 | 4A | 4B | 4C |
|---|---|---|---|---|---|
| 1 | 1 | 1 | 1 | 1 | |
| 1 | 1 | -1 | 1 | -1 | |
| 1 | 1 | 1 | -1 | -1 | |
| 1 | 1 | -1 | -1 | 1 | |
| 4 | -4 | 0 | 0 | 0 |
References
-
GroupNames, Q8,
Matrix representation
There are lots of different ways of defining . One is that it is the subgroup of generated by the matrices
and
In this form it is a nice exercise to derive a presentation of . Clearly and is not in as is easiy checked, so the order of this group must be at least 8.
We note that and that , so a guess for a presentation would be
Let us call the group presented by this presentation, then there is an obvious epimorphism from to sending to and to . This is an isomorphism as will be clear if we show that the order of is less than of equal to 8. Now every element of can be written in the form with and , since so powers of can be shifted to the right in any expression and then if the resulting power of is greater than 2 we can use to replace even powers of by powers of . We must therefore have that the group must contain at most 8 elements so the above presentation is a presentation of .
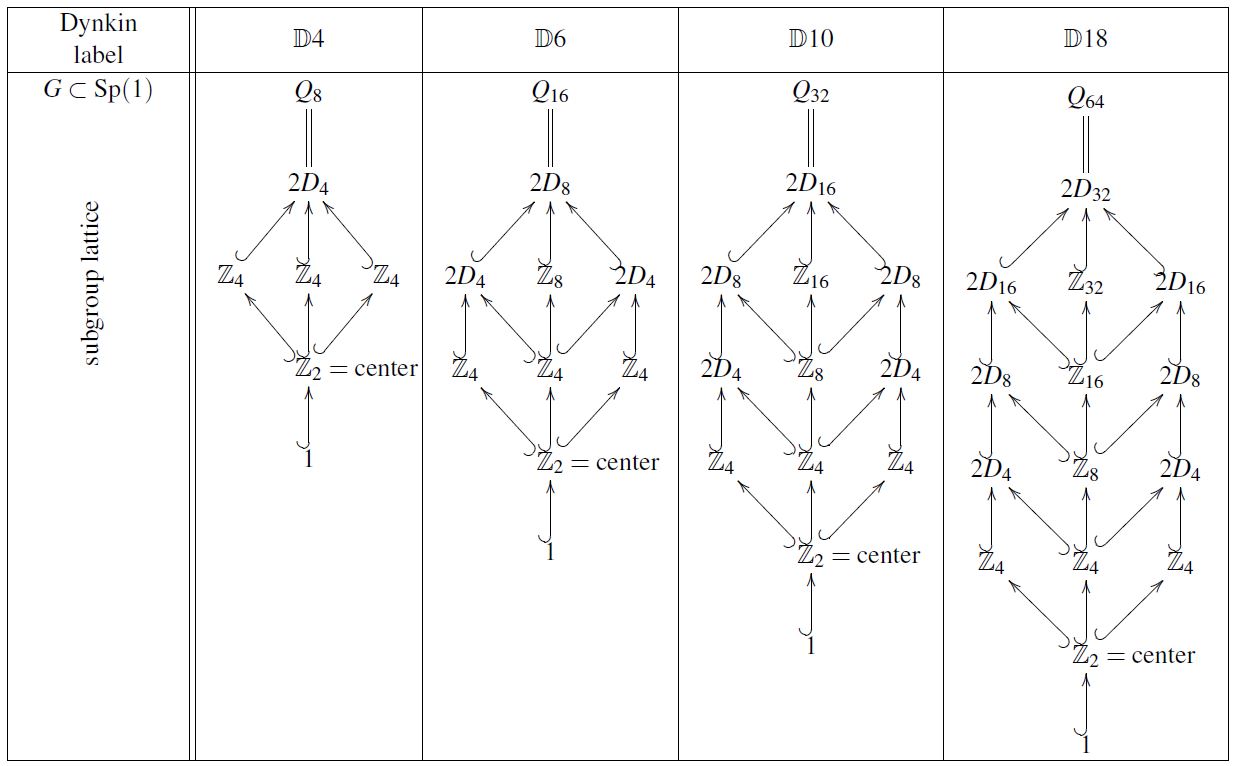
Subgroup lattice
The following shows the subgroup lattices of the first few generalized quaternion groups:
Group cohomology
The group cohomology of the generalized quaternion groups: see Tomoda & Zvengrowski 2008
Related entries
References
-
Kenneth S. Brown, Cohomology of Groups , GTM 87 Springer Heidelberg 1982. (pp.98-101)
-
H. S. M. Coxeter, The binary polyhedral groups, and other generalizations of the quaternion group , Duke Math. J. 7 no.1 (1940) pp.367–379.
-
T. Y. Lam, Hamilton’s Quaternions , pp.429-454 in Handbook of Algebra III , Elsevier Amsterdam 2004. (preprint)
-
W. R. Scott, Group Theory , Dover New York 1987. (pp.189-194, 252-254)
-
Charles Weibel, Survey of Non-Desarguesian Planes , Notices of the AMS 54 no.10 (2007) pp.1294–1303. (pdf)
-
Mehmet Koca, Ramazan Koç, Nazife Ozdes Koca, Two groups and of order 1344 (arXiv:1612.06107)
-
H.S.M. Coxeter, W. O. J. Moser, Generators and Relations for Discrete Groups, (Springer Verlag, 1965);
-
H.S.M. Coxeter, Regular Complex Polytopes (Cambridge; Cambridge University Press, 1973).
See also
On the group cohomology:
- Satoshi Tomoda, Peter Zvengrowski, Remarks on the cohomology of finite fundamental groups of 3-manifolds, Geom. Topol. Monogr. 14 (2008) 519-556 (arXiv:0904.1876)
Discussion of equivariant ordinary cohomology (Bredon cohomology) over the point but in arbitrary RO(G)-degree for equivariance group the quaternion group:
- Yunze Lu, On the -graded coefficients of equivariant cohomology, Topology and its Applications, 2021 (doi:10.1016/j.topol.2021.107921)
Last revised on December 22, 2021 at 16:03:53. See the history of this page for a list of all contributions to it.