nLab triality

Idea

The Dynkin diagram/Dynkin quiver D4 has an S3-symmetry group

(graphics grabbed from Wikipedia here)

This manifests itself in “triality” symmetries enjoyed by the objects that are labeled by D4 in an ADE-classification.

Specifically for the simple Lie group SO(8) corresponding to D4, triality is the statement that the two spin representations of the corresponding spin group $Spin(8)$ and the defining vector representations are all isomorphic, and in a nice way.

Details

Triality of subgroups of $Spin(8)$ and $SO(8)$

Proposition

(Spin(7)-subgroups in Spin(8))

There are precisely 3 conjugacy classes of Spin(7)-subgroups inside Spin(8), and the triality group $Out(Spin(8))$ acts transitively on these three classes.

(Varadarajan 01, Theorem 5 on p. 6, see also Kollross 02, Prop. 3.3 (1))

Proposition

(G₂ is intersection of Spin(7)-subgroups of Spin(8))

The intersection inside Spin(8) of any two Spin(7)-subgroups from distinct conjugacy classes of subgroups (according to Prop. ) is the exceptional Lie group G₂, hence we have pullback squares of the form

(Varadarajan 01, Theorem 5 on p. 13)

Proposition

We have the following commuting diagram of subgroup inclusions, where each square exhibits a pullback/fiber product, hence an intersection of subgroups:

Here in the bottom row we have the Lie groups

Spin(5)$\hookrightarrow$ Spin(6) $\hookrightarrow$ Spin(7) $\hookrightarrow$ Spin(8)

with their canonical subgroup-inclusions, while in the top row we have

SU(2)$\hookrightarrow$ SU(3) $\hookrightarrow$ G₂ $\hookrightarrow$ Spin(7)

and the right vertical inclusion $B \iota'$ is the delooping of one of the two non-standard inclusions, according to Prop. .

Proof

The square on the right is that from Prop. .

The square in the middle is Varadarajan 01, Lemma 9 on p. 10.

The statement also follows with Onishchik 93, Table 2, p. 144:

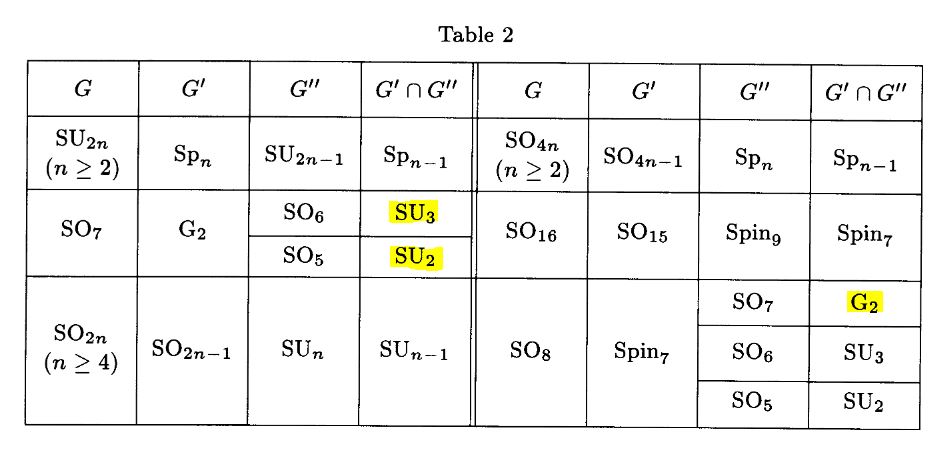
Proposition

(Spin(5).Spin(3)-subgroups in SO(8))

The direct product group SO(3) $\times$ SO(5) together with the groups Sp(2).Sp(1) and $Sp(1) \cdot Sp(2)$, with their canonical inclusions into SO(8), form 3 conjugacy classes of subgroups inside SO(8), and the triality group $Out(Spin(8))$ acts transitively on these three classes.

(Kollross 02, Prop. 3.3 (3))

Similarly:

Proposition

(Spin(5).Spin(3)-subgroups in Spin(8))

The groups Spin(5).Spin(3), Sp(2).Sp(1) and $Sp(1) \cdot Sp(2)$, with their canonical inclusions into Spin(8), form 3 conjugacy classes of subgroups inside Spin(8), and the triality group $Out(Spin(8))$ acts transitively on these three classes.

(Čadek-Vanžura 97, Sec. 2)

In summary we have these subgroup inclusions

permuted by triality:

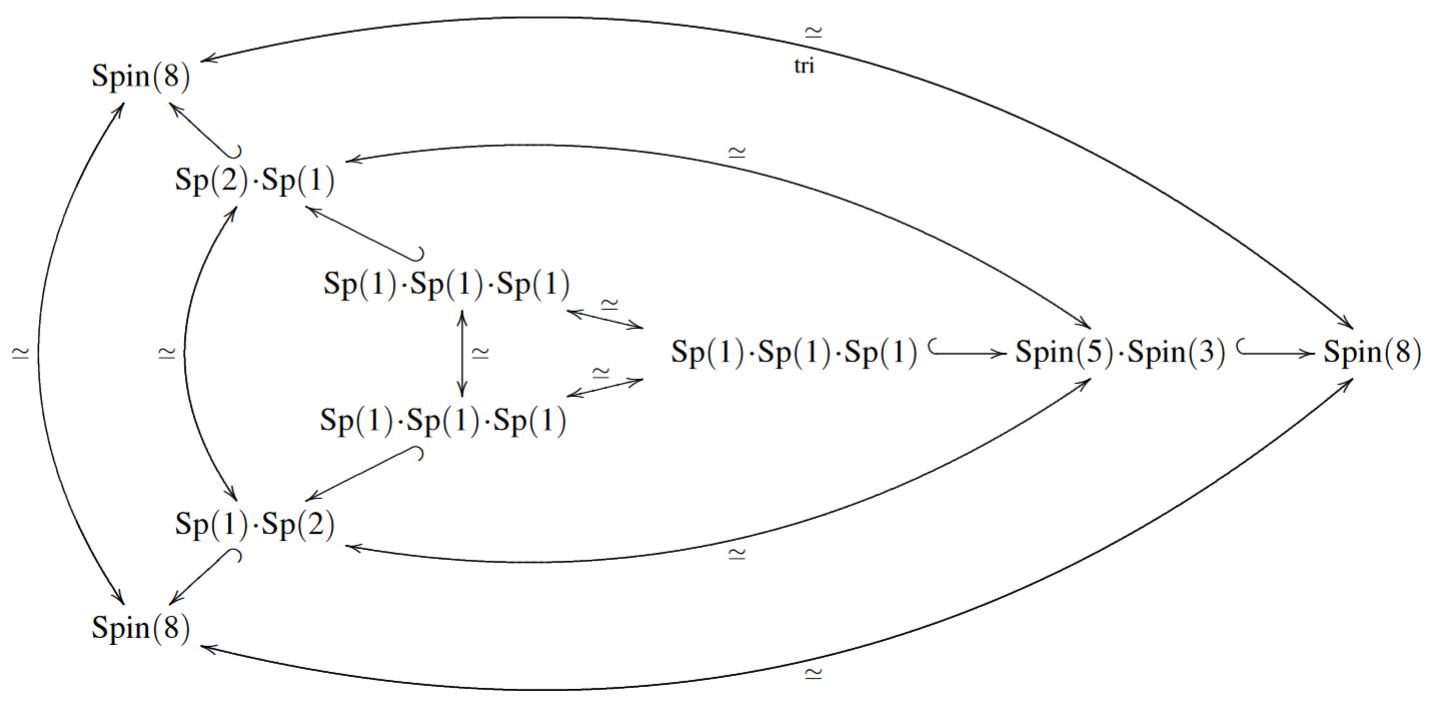
graphics grabbed from FSS 19, Sec. 3.3

References

General

• Tonny Springer, Ferdinand Veldkamp, chapter 3 of Octonions, Jordan Algebras, and Exceptional Groups, Springer Monographs in Mathematics, 2000

Discussion of triality of subgroups of Spin(8) and SO(8):

• Veeravalli Varadarajan, Spin(7)-subgroups of SO(8) and Spin(8), Expositiones Mathematicae Volume 19, Issue 2, 2001, Pages 163-177 (doi:10.1016/S0723-0869(01)80027-X, pdf)

• Martin Čadek, Jiří Vanžura, On $Sp(2)$ and $Sp(2) \cdot Sp(1)$-structures in 8-dimensional vector bundles, Publicacions Matemàtiques Vol. 41, No. 2 (1997), pp. 383-401 (jstor:43737249)

• Megan M. Kerr, New examples of homogeneous Einstein metrics, Michigan Math. J. Volume 45, Issue 1 (1998), 115-134 (euclid:1030132086)

• Andreas Kollross, Prop. 3.3 of A Classification of Hyperpolar and Cohomogeneity One Actions, Transactions of the American Mathematical Society Vol. 354, No. 2 (Feb., 2002), pp. 571-612 (jstor:2693761)

See also

• Wikipedia, Triality

• John Baez, Spinors and trialities

In string theory

Exposition with an eye to application in string theory:

• David Tong, Carl Turner, Notes on 8 Majorana Fermions (arXiv:1906.07199)

Discussion in the foundations of M-theory:

• Domenico Fiorenza, Hisham Sati, Urs Schreiber, Section 3.3 of Twisted Cohomotopy implies M-theory anomaly cancellation (arXiv:1904.10207)