nLab ring object
Context
Categorical algebra
internalization and categorical algebra
-
algebra object (associative, Lie, …)
Contents
Idea
For a cartesian monoidal category (a category with finite products), an internal ring or a ring object in is an internalization to the category of the notion of a ring.
Under some reasonable assumptions on that allow one to construct a (symmetric) monoidal tensor product on the category of abelian group objects internal to , a ring object can also be defined as a monoid object internal to that monoidal category .
Sometimes one might take this last point of view a little further, especially in certain contexts of stable homotopy theory where a stable (∞,1)-category of spectra is already something like an (∞,1)-category-analogue of a category of abelian groups. With the understanding that a symmetric smash product of spectra plays a role analogous to tensor products of abelian groups, monoids with respect to the smash product are often referred to as “-rings” of one sort or another (as mentioned at “ring operad”). Thus we have carry-over phrases from the early days of stable homotopy theory, such as “A-∞ rings” (for monoids) and “E-∞ rings” (commutative monoids). Here it is understood that the monoid multiplication on spectra is an -refinement of a multiplicative structure on a corresponding cohomology theory, with various forms of K-theory providing archetypal examples.
Definition
Traditional definition
The traditional definition, based on a traditional presentation of the equational theory of rings, is that a ring object consists of an object in a cartesian monoidal category together with morphisms (addition), (multiplication), (zero), (multiplicative identity), (additive inversion), subject to commutative diagrams in that express the usual ring axioms.
As a model of a Lawvere theory
Let be the Lawvere theory for rings, viz. the category opposite to the category of finitely generated free rings (which are non-commutative polynomial rings ) and ring maps between them. Then for a category with finite products, a ring object in may be identified with a product-preserving functor .
Via the microcosm principle
Alternatively, one may define ring objects following the Baez–Dolan microcosm principle. Indeed, similarly to how it is possible to define monoids in a monoidal category (a pseudomonoid in ), it is possible to speak of rig objects internal to any bimonoidal category (a pseudomonoid in ).
Namely, a rig in a bimonoidal category is given by a quintuple consisting of
- An object of , called the underlying object of the rig;
- A morphism
of , called the addition morphism of ;
- A morphism
of , called the multiplication morphism of ;
- A morphism
of , called the additive unit morphism of ;
- A morphism
of , called the multiplicative unit morphism of ;
satisfying the following conditions:
-
The triple is a commutative monoid in ;
-
The triple is a monoid in ;
-
The diagrams
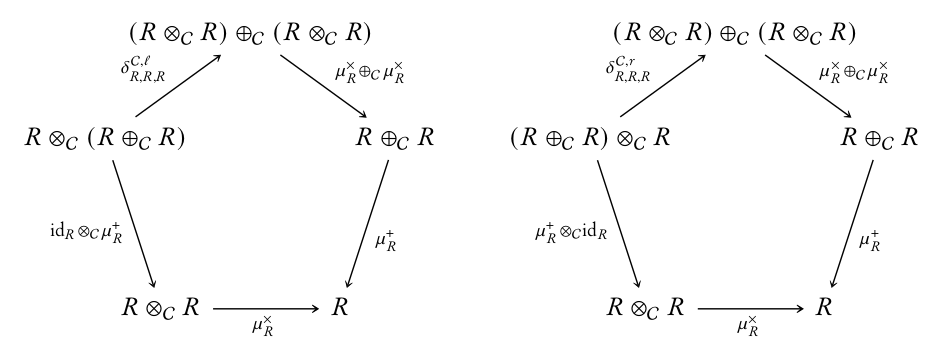
corresponding to the rig axioms and commute;
-
The diagrams
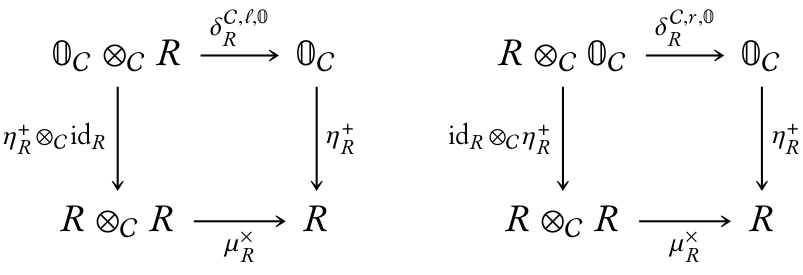
corresponding to the rig axioms and commute;
Moreover, for a braided bimonoidal category, one defines a commutative rig in to be a rig in whose multiplicative monoid structure is commutative.
A partial version of this definition first appeared in (Brun 2006, Definition 5.1).
Examples
-
A ring object in Top is a topological ring.
-
A topos equipped with a ring object is called a ringed topos, see there for more details.
-
The affine line (see there) is a ring object in the given ambient topos.
For the notion of a rig in a bimonoidal category defined via the microcosm principle, we have the following examples.
- A rig in is a monoid.
- A rig in is a rig.
- A rig in is a ring.
- A rig in is an associative algebra.
- A rig in is a strict monoidal category.
Related concepts
-
ring, ring object
References
- Morten Brun, Witt Vectors and Equivariant Ring Spectra, 2006. Proceedings of the London Mathematical Society, Volume 94, pp. 351–385. (arXiv:math/0411567, doi:10.1112/plms/pdl010.)
Last revised on July 25, 2023 at 11:38:52. See the history of this page for a list of all contributions to it.