nLab structure
This entry is about a general concepts of “mathematical structure” such as formalized by category theory and/or dependent type theory. This subsumes but is more general than the concept of structure in model theory.
Context
Mathematics
-
-
- geometry (general list), topology (general list)
- general topology
- differential topology
- differential geometry
- algebraic geometry
- noncommutative algebraic geometry
- noncommutative geometry (general flavour)
- higher geometry
Mathematics
-
-
- geometry (general list), topology (general list)
- general topology
- differential topology
- differential geometry
- algebraic geometry
- noncommutative algebraic geometry
- noncommutative geometry (general flavour)
- higher geometry
Contents
Idea
It is common in informal language to speak of mathematical objects “equipped with extra structure” of some sort. The archetypical examples are algebras over a Lawvere theory in Set: these are sets equipped with the structure of certain algebraic operations. For instance a group is a set equipped with a binary operation , etc.
One may formalize the notion of structure using the language of category theory. This is discussed at stuff, structure, property. In that formalization objects in some category are objects in some category equipped with extra structure if there is a functor such that
- is a faithful functor.
Depending on author and situation, more properties are required of this functor (Ehresmann 57, Ehresmann 65, Adamek-Rosicky-Vitale 09, remark 13.18):
-
is an amnestic functor (-vertical isomorphisms are identities),
-
is an isofibration (isomorphisms can be lifted along ).
However, notice that these two conditions violate the principle of equivalence for categories. In the terminology of strict categories one might hence refer to these conditions as expressing “strict extra structure”.
Notions of structure
A special class of examples of this is the notion of structure in model theory. In this case one defines a “language” that describes the constants, functions (say operations) and relations with which we want to equip sets, and then sets equipped with those operations and relations are called -structures for that language. (Equivalently one might say “sets with -structure”. Or one might generally say “-structure” for “set with -structure”.) In this case there is a faithful functor from -structures to their underlying sets, and so this is a special case of the general definition.
We instead say model of a theory when we restrict to those structures which satisfy the axioms of a theory (in other words, satisfy properties specified by the axioms). In this case there is a full and faithful functor from the category of models of a theory to the category of structures of the underlying language , while the composition of forgetful functors
is again faithful.
Remarks
Thus, the English word “structure” is used in several slightly differing mathematical senses.
-
Within category theory itself, “structure” can function as a kind of mass noun, as in a phrase like “forgetting structure”. Here it refers to data comprising operations, relations, constants, and also properties borne by models of a theory or relative theory, considered abstractly (for example, the functor which forgets group structure, or the functor which forgets multiplicative structure). On the other hand, it can also operate in the singular, where one says for example “a topological group is a topological space equipped with a group structure, such that…”
-
In model theory, however, the term structure is not a mass noun; it refers to a particular set (or “structures” for a family of sets) together with functions, relations, and elements that interpret the symbols of operations, predicates, and constants of a language. When one adds axioms to a language to make a theory, then a structure of the language where those axioms get interpreted as properties satisfied by the structure is called a model of the theory. Thus, in summary, the category theorist might refer to “the structure of a group” as consisting of a multiplication, a unit, etc., satisfying group axioms, while the model theorist would say that each particular group (like ) is a model of a theory of groups. For a model theorist, being a model does entail being a structure for the language of groups, but she would also say that a structure for the language of groups need not satisfy any of the axioms of a group (like associativity or unitality).
Examples
There are gazillions of examples of objects equipped with extra structure. The most familiar is maybe
Generally the forgetful functor from a category of algebras over an algebraic theory down to the base category exhibits the equipment with the corresponding algebraic structure.
Structures in dependent type theory
In dependent type theory the notion of “mathematical structure” and/or data structure on a base is given by iterated dependent pairings (hence forming “type telescopes” also called “records” in Coq) with -dependent types encoding operations on/with this type together with their behavioural specification.
The following shows some examples, using the notation for dependent pairs from here.
Via the extensionality principles for dependent pairs (here) and for dependent functions (here) such type theoretic structure automatically obey the structure identity principle:
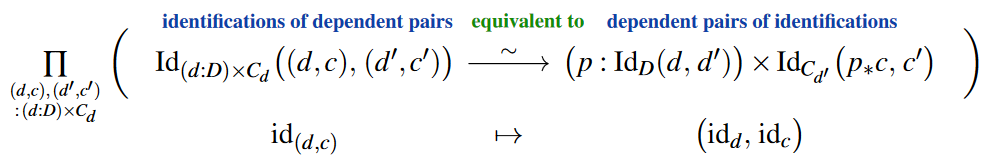

In that any equivalence/identification between pairs of data of the following types are isomorphisms in the sense of bijective homomorphisms.
Lensed data structure
To say that a given data (base) type is
-
equipped with
-
such that this does behave as expected, namely as a well-behaved -lens-structure on
means to declare it to be of the following iterated dependent pair-telescope type:

Group data structure
The dependent pair-telescope type declaration of group structure:
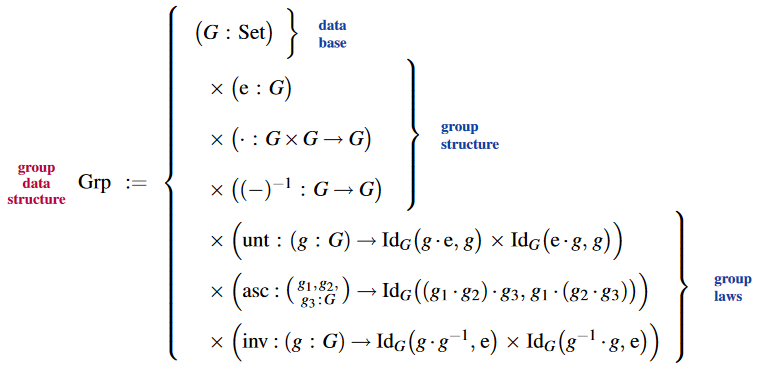
Further restriction to abelian groups:
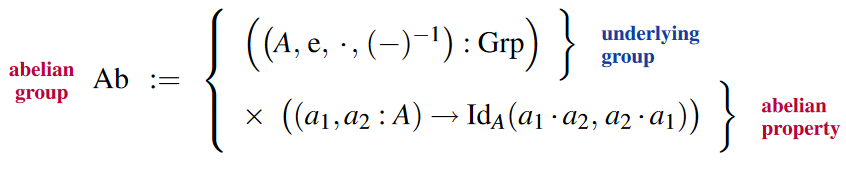
Via the structure identity principle (above), the identitifications/equivalences between such group data types are indeed bijective group homomorphisms, hence group-isomorphisms:
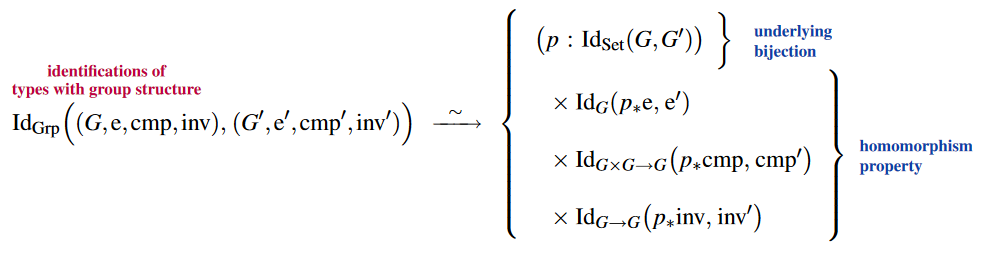
The structure of subgroups of a given group structure:
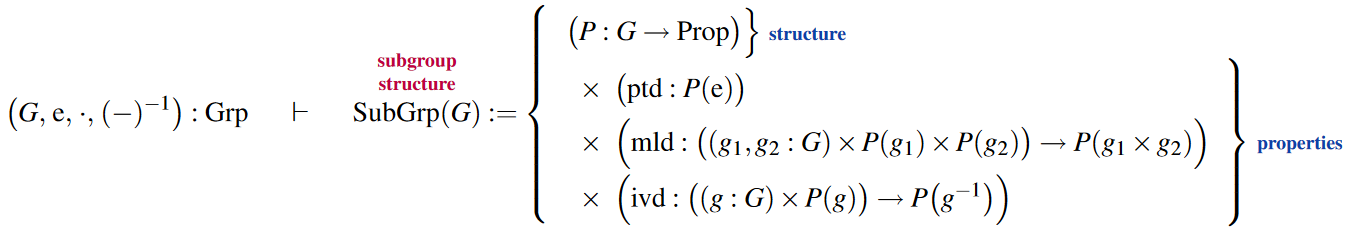
and their underlying abstract group structure:

Group action structure
The dependent pair-telescope type declaration of group actions on sets (G-sets):
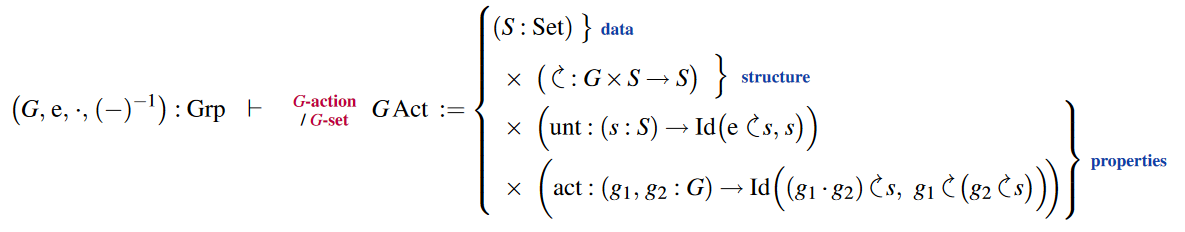
Specialization to torsors:
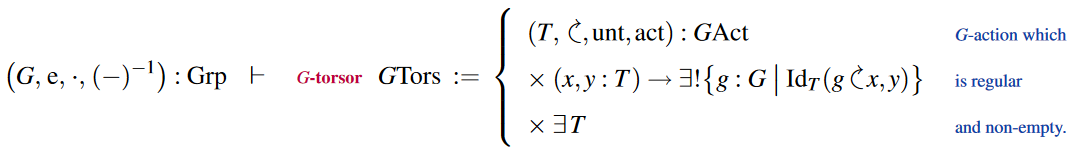
Ring data structure
The dependent pair-telescope type declaration of unital ring structure:

For examples see at numbers – In dependent type theory.
Module data structure
Given a unital ring type (as above), the type of -module objects is the following dependent pair-telescope:

Higher structures in homotopy type theory
The above examples of structures formulated in dependent type theory all had data sets as their base, which is the classical situation. But in dependent type theory with untruncated identification types, hence in homotopy type theory, we may simply drop this constraint and consider structures whose base is any higher homotopy type: This yields the notion of higher structures.
Delooping
Given a set-based group structure (as above), delooping structure is
(…)
Higher delooping
More generally, one may consider delooping of -groups, but this is a lot of (higher) structure if spelled out in detail. Yet more generally and again more readily axiomatized there is the notion of deloopings of any pointed types (cf. Wärn (2023, §2), BCFR23), which we may write as follows:
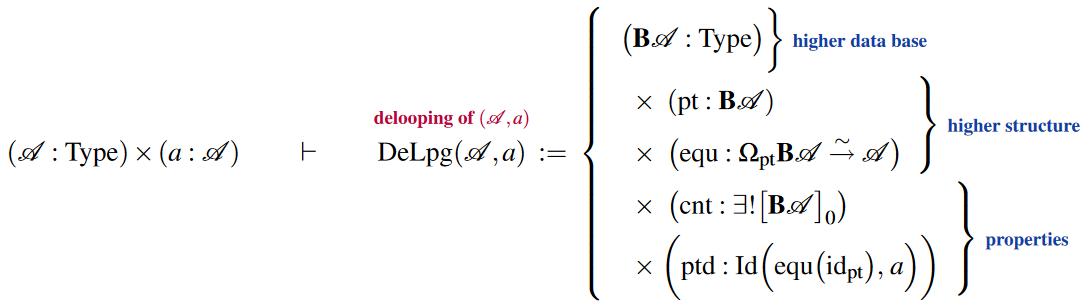
Similarly there is iterated delooping structure:
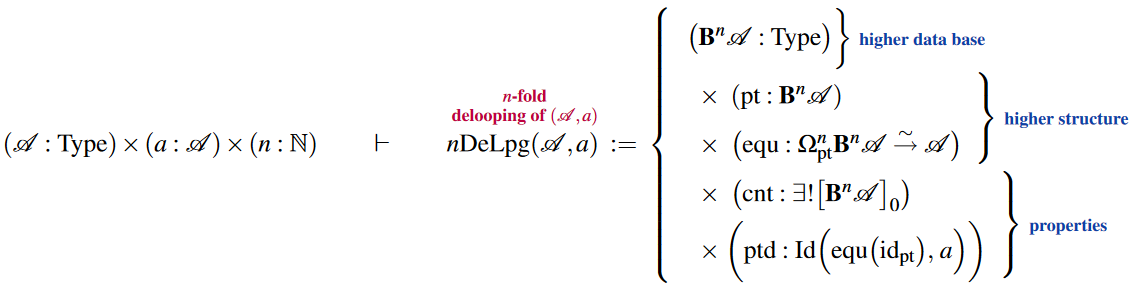
Related entries
-
Evident as the notion of mathematical structure may seem these days, it was at least not made explicit until the middle of the 20th century. Then it was the influence of the Bourbaki-project (see there for more) and then later the development of category theory which made the notion explicit and finally led to the above formalization.
-
functions that preserves extra structure are called homomorphisms; relations that preserve extra structure are called logical relations_
References
General
On the history of the notion of “mathematical structure” with some focus on what Bourbaki did and did not contribute to the subject:
-
Leo Corry, Mathematical Structures from Hilbert to Bourbaki: The Evolution of an Image of Mathematics, in: Changing Images of Mathematics in History. From the French Revolution to the new Millenium Harwood Academic Publishers (2001) 167-186 [ISBN:9780415868273, pdf]
-
Leo Corry, Modern Algebra and the Rise of Mathematical Structures, Springer (2004) [doi:10.1007/978-3-0348-7917-0]
See also
-
Wikipedia, Mathematical structure
-
Wikipedia, Structure_(mathematical_logic)
Early proposal to grasp the notion of mathematical structures via category theory (specifically via forgetful functors between groupoids):
-
Charles Ehresmann, Gattungen in Lokalen Strukturen, Jahresbericht der Deutschen Mathematiker-Vereinigung 60 (1958) 49-77 [dml:146434]
-
Charles Ehresmann, Catégories et Structures, Séminaire Ehresmann. Topologie et géométrie différentielle 6 (1964) 1-31 [numdam:SE_1964__6__A8_0, dml:112200]
For modern accounts on mathematical structures via categorical algebra see also at algebraic theory, monad, sketch.
In dependent type theory
Discussion of mathematical structures via dependent type theory:
the general idea of representing mathematical structures as type telescopes:
-
Jeffery Zucker, Formalization of Classical Mathematics in Automath, Colloques Internationaux du Centre National de la Recherche Scientifique 249 (1975) 135-145 [web, pdf]
also in: Studies in Logic and the Foundations of Mathematics 133 (1994) 127-139 [doi:10.1016/S0049-237X(08)70202-7]
-
Nicolaas de Bruijn, Telescopic mappings in typed lambda calculus, Information and Computation 91 2 (1991) 189-204 [doi:10.1016/0890-5401(91)90066-B]
and with emphasis of the notion of isomorphism between such structures:
- David McAllester, Dependent Type Theory as Related to the Bourbaki Notions of Structure and Isomorphism [arXiv:2104.08958]
in Coq:
-
Herman Geuvers, Randy Pollack, Freek Wiedijk, Jan Zwanenburg, A Constructive Algebraic Hierarchy in Coq, Journal of Symbolic Computation 34 4 (2002) 271-286 [doi:10.1006/jsco.2002.0552, pdf]
-
Claudio Sacerdoti Coen, Enrico Tassi, Working with Mathematical Structures in Type Theory, in: Types for Proofs and Programs. TYPES 2007, Lecture Notes in Computer Science 4941 Springer (2008) [doi:10.1007/978-3-540-68103-8_11, pdf]
-
François Garillot, Georges Gonthier, Assia Mahboubi & Laurence Rideau, Packaging Mathematical Structures, in: Theorem Proving in Higher Order Logics. TPHOLs 2009, Lecture Notes in Computer Science 5674, Springer (2009) [doi:10.1007/978-3-642-03359-9_23]
-
Bas Spitters, Eelis van der Wegen Type classes for mathematics in type theory, Mathematical Structures in Computer Science 21 4 “Interactive Theorem Proving and the Formalisation of Mathematics” (2011) 795-825 [doi:10.1017/S0960129511000119, arXiv:1102.1323]
(via Type classes)
-
Kazuhiko Sakaguchi, Validating Mathematical Structures, in Automated Reasoning. IJCAR 2020, Lecture Notes in Computer Science 12167, Springer (2020) [doi:10.1007/978-3-030-51054-1_8]
in Lean:
- The mathlib Community, §4 in: The Lean mathematical library, in CPP 2020: Proceedings of the 9th ACM SIGPLAN International Conference on Certified Programs and Proofs (2020) 367–381 [arXiv:1910.09336, doi:10.1145/3372885.3373824]
Discussion of classes of mathematical structures in univalent homotopy type theory (univalent foundations of mathematics) which satisfy a structure identity principle:
-
Thierry Coquand, Nils Anders Danielsson, Isomorphism is equality, Indagationes Mathematicae 24 4 (2013) 1105-1120 [doi:10.1016/j.indag.2013.09.002]
-
Univalent Foundations Project, §9.8 but also §2 of: Homotopy Type Theory – Univalent Foundations of Mathematics (2013) [web, pdf]
-
Martín Escardó, A structure identity principle for a standard notion of structure, §3.33.1 in: Introduction to Univalent Foundations of Mathematics with Agda [arXiv:1911.00580, webpage]
(formalized in the Agda proof assistant)
-
Benedikt Ahrens, Paige Randall North, Michael Shulman, Dimitris Tsementzis, A Higher Structure Identity Principle, LICS ‘20 (2020) 53–66 [arXiv:2004.06572, doi:10.1145/3373718.3394755]
Discussion in the context of the philosophy of structuralism:
- Dimitris Tsementzis, §5.1 in: Univalent foundations as structuralist foundations, Synthese 194 9 (2017) 3583–3617 [jstor:26748765, doi:10.1007/s11229-016-1109-x, pdf]
Expressions towards the notion that, thereby the notions of mathematical structures are data structures may be understood to coincide (just along the lines of types being data types):
- Thomas Kehrenberg, Basic building blocks of dependent type theory (Dec. 2022) [post on LessWrong, post on personal blog]
“An example of a use case for non-binary sum types is the definition of mathematical “data structures” like a ring or a group. These data structures are usually defined as…”
Last revised on February 20, 2023 at 04:39:29. See the history of this page for a list of all contributions to it.