Schreiber Equivariant principal infinity-bundles

A book that we are finalizing:

---

• Hisham Sati and Urs Schreiber:

  
  

  Equivariant Principal $\infty$-Bundles

  
  

  download:

  • v2: pdf

  • arXiv:2112.13654

---

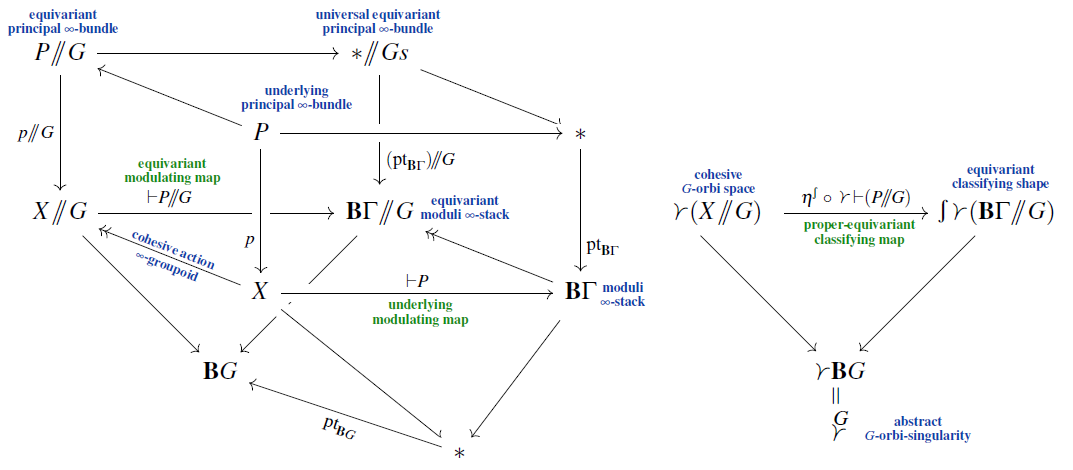
on the joint generalization of

1. equivariant principal bundles

2. principal ∞-bundles

in

• singular-cohesive homotopy theory.

$\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;$ What this book is about.

In this book we prove classification results for stable equivariant $\Gamma$-principal bundles in the case when the underlying homotopy type $\esh \, \Gamma$ of the topological structure group $\Gamma$ is truncated, meaning that its homotopy groups vanish in and above some degree $n$. We discuss how this coincides with the classification of equivariant higher non-abelian gerbes and generally of equivariant principal $\infty$-bundles with structure $n$-group $\esh \Gamma$; and we show how the equivariant homotopy groups of the respective classifying $G$-spaces are given by the non-abelian group cohomology of the equivariance group with coefficients in $\esh \Gamma$.

The result is proven in a conceptually transparent manner as a consequence of a smooth Oka principle which becomes available after faithfully embedding traditional equivariant topology into the singular-cohesive homotopy theory of globally equivariant higher stacks. This works for discrete equivariance groups $G$ acting properly on smooth manifolds (“proper equivariance”) with resolvable singularities whence we are equivalently describing principal bundles on good orbifolds.

In setting up this proof, we re-develop the theory of equivariant principal bundles from scratch by systematic use of Grothendieck‘s internalization. In particular we prove that all the intricate equivariant local triviality conditions considered in the literature are automatically implied by regarding $G$-equivariant principal bundles as principal bundles internal to the $B G$-slice of the ambient cohesive $\infty$-topos. We also show that these conditions are all equivalent. Generally we find that the characteristic subtle phenomena of equivariant classifying theory all reflect basic modal properties of singular-cohesive homotopy theory (hence of cohesive global equivariant homotopy theory).

An archetypical example is the infinite projective unitary structure group $\Gamma = PU(\mathcal{H})$, in which case we are classifying the degree-3 twists of equivariant $\KU$-theory (related to equivariant “bundle gerbes”), recovering the results of BEJU14, Thm. 1.10, LüUr14, Thm. 15.17. Our general theorem immediately enhances this to the conjugation-equivariant graded projective unitary structure group $\mathbb{Z}/2 \curvearrowright \, PU(\mathcal{H})_{gr}$ with fixed locus $PU(\mathcal{H})_{gr}^{\mathbb{Z}/2} \,=\, PO(\mathcal{H}_{\mathbb{R}})$, where we are classifying the twists of equivariant KR-theory in degrees 1 and 3 combined, restricting on “O-planes” to the twists of $KO$-theory in degrees 1 and 2 combined. This is the generality in which equivariant K-theory twists are conjectured to model the B-field in string theory on orbi-orientifolds.

Our focus on the class of truncated structure groups is largely complementary to the classical literature on equivariant classifying spaces, which is mostly concerned with the class of compact Lie structure groups $\Gamma$. The two classes intersect when $\Gamma = T^d \rtimes K$ is the extension of a finite group $K$ by a compact abelian Lie group, i.e., the case of equivariant sheeted torus bundles (“bundle 0-gerbes”). In this case our general classification recovers the results of LMS84, Lem. 1, Thm. 2, May 90, Thm. 3, Thm. 10, Rez16, Thm. 1.2 and generalizes them to the case of non-trivial $G$-action on $\Gamma$.

A classification result for general topological structure groups had previously been claimed in MurSh95 but, as highlighted in GMM17, 3.12, the proof had remained open. Besides proving its classification property for truncated structure groups, we show that the Murayama-Shimakawa construction of MurSh95 generally produces the underlying equivariant homotopy type of the correct equivariant moduli stacks.

While compact Lie structure groups $\Gamma$ have received much attention due to the role of equivariant vector bundles as cocycles of equivariant K-theory, the complementary case of truncated structure groups $\Gamma$ that we discuss will generally be relevant for equivariant bundles in their role as twists of equivariant generalized cohomology theories, since such twists will typically be considered in a finite number of degrees, with $\esh \Gamma$ a truncation of the $\infty$-group of units of a ring spectrum. This combined twisted \ equivariant enhancement of generalized cohomology theory has previously received little attention (except for a brief note in Lind 14) beyond the example of $\KU$-theory. We mean this book to be laying previously missing foundations.

In particular, the equivariant classifying spaces produced here provide the correct domains for twisted equivariant Chern-Dold character maps, and hence allow the systematic definition and construction of twisted equivariant differential generalized cohomology theories in equivariant generalization of the construction in FSS20. This will be discussed elsewhere.

---

Related articles:

• Hisham Sati, Urs Schreiber:

  Proper Orbifold Cohomology

  arXiv:2008.01101

• T. Nikolaus, U. Schreiber, D. Stevenson:

  Principal ∞-bundles

  arXiv:1207.0248, arXiv:1207.0249

• Hisham Sati, Urs Schreiber:

  Anyonic defect branes in TED-K-theory

  arXiv:2203.11838

Related talks:

• Higher and Equivariant Bundles

  talk via Feza Gürsey Higher Structures Seminar,

  Feza Gürsey Institute Istanbul, 2022

• Twisted equivariant differential (TED) K-theory via diffeological stacks

  talk at Global Diffeology Seminar, 03 Nov 2022

  slides: pdf

---