nLab wallpaper group

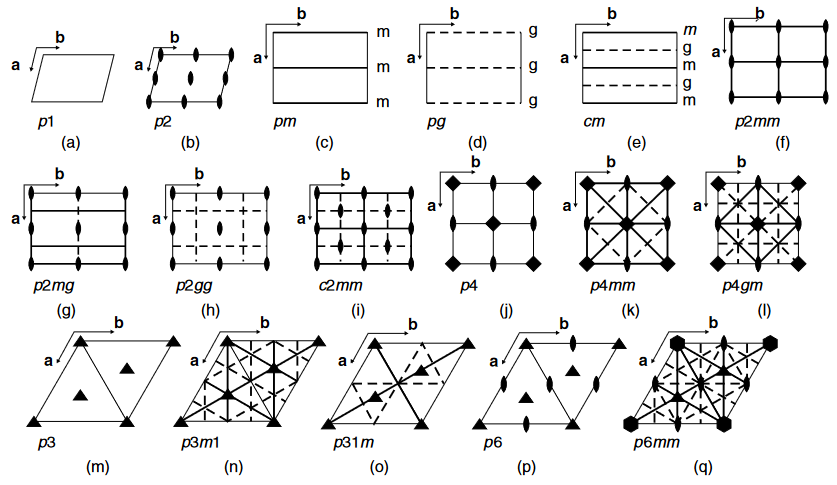
Definition

A wallpaper group is a crystallographic group (space group) in dimension 2, hence a subgroup $G \subset Iso(\mathbb{R}^2)$ of the isometry group of the Euclidean plane such that

1. the part of $G$ inside the translation group is generated by two linearly independent vectors;

2. the point group is finite.

Fig. 3.10 in Tilley 2020:

Related concepts

• flat orbifold

• finite rotation group

• tesselation

References

e. g.

• Richard Tilley, Sec. 3.5 in: Crystals and Crystal Structure, Wiley (2020) [ISBN:978-1-119-54838-6]

• Patrick Morandi, The Classification of Wallpaper Patterns: From Group Cohomology to Escherís Tessellations (pdf)

See also

• Wikipedia, Wallpaper group

Discussion of meromorphic functions on the complex plane invariant under wallpaper groups:

• Richard Chapling, Invariant Meromorphic Functions on the Wallpaper Groups (arXiv:1608.05677)