Contents
Context
Universes
Type theory
Contents
Idea
The boolean domain or boolean field (often just: ) is a -element set, say (“bits”) or (“bottom”, “top”), whose elements may be interpreted as truth values.
Note that is the set of all truth values in classical logic, but this cannot be assumed in non-classical logic such as intuitionistic logic.
The Boolean domain plays the role of the subobject classifier in the Boolean topos of Sets.
If we think of the classical as a pointed set equipped with the true element, then there is an effectively unique boolean domain.
A boolean variable is a variable that takes its value in a boolean domain, as . If this variable depends on parameters, then it is (or defines) a Boolean-valued function, that is a function whose target is .
An element of is a binary digit, or bit.
The boolean domain is the initial set with two elements. It is also the initial set with an element and an involution. It is also the tensor unit for the smash product in the monoidal category of pointed sets.
Definition
In type theory
As an inductive type, the boolean domain is given by
Inductive Bool : Type
| zero : Bool
| one : Bool
This says that the type is inductively constructed from two terms in the type Bool, whose interpretation is as the two points of the type.
As a positive type
Assuming that identification types and dependent product types exist in the type theory, the boolean domain is the inductive type generated by two elements, and is defined by the following inference rules:
type formation rules for the boolean domain
term introduction rules for the boolean domain:
term elimination rules for the boolean domain:
computation rules for the boolean domain:
uniqueness rules for the boolean domain:
- judgmental uniqueness rules
- typal uniqueness rules
The elimination, typal computation, and typal uniqueness rules for the boolean domain state that the boolean domain satisfies the dependent universal property of the boolean domain. If the dependent type theory also has dependent sum types and product types, allowing one to define the uniqueness quantifier, the dependent universal property of the boolean domain can be simplified to the following rule:
The judgmental computation and uniqueness rules imply the typal computation and uniqueness rules and thus imply the dependent universal property of the boolean domain.
In type theories with a separate type judgment where not all types are elements of universes, one has to additionally add the following elimination and computation rules:
Elimination rules:
Computation rules:
- judgmental computation rules
As the type of decidable propositions
The boolean domain can also be defined as the type of decidable propositions. Suppose that we have a type of propositions . Then, the type of booleans is defined as
where is the disjunction of two types and and is the negation of the type . Both disjunctions and the empty set can be directly defined from , dependent function types, and product types.
One can also define directly the boolean domain as the type of all decidable propositions, provided one already has disjunctions defined in the type theory. Similarly to the type of all propositions, the boolean domain can be presented either as a Russell universe or a Tarski universe. The difference between the two is that in the former, every decidable proposition in the type theory is literally an element of the boolean domain, while in the latter, elements of are only indices of a (-1)-truncated type family ; every decidable proposition in the type theory is only essentially -small for weak Tarski universes or judgmentally equal to an for for strict Tarski universes.
As a strict Tarski universe
As a strict Tarski universe, the boolean domain is given by the following natural deduction inference rules:
Formation rules for the boolean domain:
Introduction rules for the boolean domain:
Elimination rules for the boolean domain:
Computation rules for the boolean domain:
- Judgmental computation rules:
Uniqueness rules for the boolean domain:
Extensionality principle for the boolean domain:
As a weak Tarski universe
As a weak Tarski universe, the boolean domain is given by the following natural deduction inference rules:
Formation rules for the boolean domain:
Introduction rules for the boolean domain:
Elimination rules for the boolean domain:
Computation rules for the boolean domain:
- Judgmental computation rules:
where the equivalences
can always be constructed in a type theory with dependent product types, dependent sum types, identity types, disjunctions, and negations, as given types and and an equivalence , it is possible to form the equivalences
through application of equivalences to identifications and the typal congruence rules of function types, dependent product types, product types, dependent sum types, disjunctions, and negations.
Uniqueness rules for the boolean domain:
Extensionality principle for the boolean domain:
As a Russell universe
As a Russell universe, the boolean domain is given by the following natural deduction inference rules:
Formation rules for the boolean domain:
Introduction rules for the boolean domain:
Elimination rules for the boolean domain:
Computation rules for the boolean domain:
- Judgmental computation rules:
Uniqueness rules for the boolean domain:
Extensionality principle for the boolean domain:
In homotopy type theory
In homotopy type theory the type of booleans / bits looks as above (using judgemental equality, propositional equality, or typal equality for the computation rule and uniqueness rule) but now it may equivalently be thought of as the sphere type of the 0-sphere and as such as the beginning of the suspension type-tower of types of “higher homotopy bits” — the -sphere types:
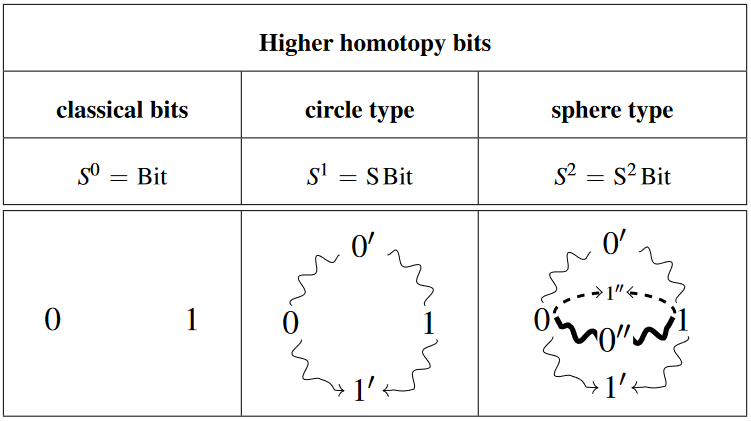
Properties
Descent and large elimination
The descent for the boolean domain states that given any types and one can construct a type family with equivalences of types
Large elimination for the boolean domain strengthens the equivalences of types in descent to judgmental equality of types
Extensionality principle of the boolean domain
The elements of the boolean domain represent certain truth values or propositions, namely, true and false. By the principle of propositions as some types, truth values or propositions are represented as certain types: specifically, true or is represented by the unit type , and false or is represented by the empty type . The boolean domain is a Tarski universe through the following type family:
The extensionality principle of the boolean domain is then given by the univalence axiom:
Since the empty type is not equivalent to the unit type, this automatically implies that is not equal to . The extensionality principle of the boolean domain can be proven from descent of the boolean domain, see Sattler 2023 for a proof.
Relation to sum types
The sum types can be defined in terms of the boolean domain and the dependent sum type. Given types and , the sum type is defined as
Boolean logic
One could recursively define the logical functions on as follows
- For negation
- For conjunction
- For disjunction
- For implication
- For the biconditional
One could prove that form a Boolean algebra. The poset structure is given by implication.
One could also inductively define observational equality on the booleans as an indexed inductive type on the boolean type with the following constructors
A boolean predicate valued in a type is a function , and the type is a boolean function algebra for finite types , and if path types exist, for all types . Thus the functor , for a type universe is a Boolean hyperdoctrine, and one could do classical first-order logic inside if and path types exist in .
In fact, just with dependent sum types, dependent product types, empty type, unit type, and the two-valued type in a type universe , any two-valued logic could be done inside . Furthermore, since binary disjoint coproducts exist when exists, all finite types exist in , and any finitely-valued logic?, such as the internal logic of a finite cartesian power of Set, could be done inside .
For finite types, one could also inductively define specific functions
from the type of boolean predicates on and such that they behave like existential quantification and universal quantification.
Other properties
As a result, sometimes the boolean domain is called a decidable subset classifier.
References
See also:
Discussion in type theory as a simple example of an inductive type:
Discussion in homotopy type theory:
…
Large elimination and descent of the boolean domain can be found in
