nLab transgression in group cohomology

Idea

For $G$ a discrete group (often taken to be a finite group) and for $A$ any (discrete) abelian group, there is a transgression homomorphism of cohomology groups

(1)$$\begin{array}{rcl} H_{grp}^{\bullet + 1}(G;\,A) \;\;=\;\; \\ H^{\bullet + 1}(B G;\, A) & \xrightarrow{ \;\;\;\; \tau \;\;\;\; } & H^n \big( \Lambda B G, \, A \big) \;\simeq \\ && \underset{ \mathclap{ \array{ \phantom{-} \\ [g] \in G^{ad}/G } } }{\oplus} \; H^n_{grp}\big(C_g;\, A \big) \end{array}$$

from the group cohomology of $G$ to the groupoid cohomology, in one degree lower, of the inertia groupoid $\Lambda B G$ of its delooping groupoid $B G \simeq (G \rightrightarrows \ast)$.

Since the inertia groupoid of the delooping groupoid is equivalent to a disjoint union over conjugacy classes $[g] \in G^{ad}/G$ of delooping groupoids of centralizer subgroups $C_g$, with $C_e = G$,

(2)$$\Lambda B G \;\simeq\; \underset{ [g] \in G_{ad}/G }{\coprod} B C_g \;\;\;\simeq\;\;\; B G \,\sqcup\, \underset{ [g] \neq [e] }{\coprod} B C_g \,,$$

this induces a corestricted transgression map within the group cohomology of $G$, and, more generally, to the group cohomology of any of its centralizer subgroups:

$$H_{grp}^{\bullet + 1}(G;\,A) \xrightarrow{ \;\;\; \tau_{[e]} \;\;\; } H_{grp}^{\bullet}(G;\,A) \,, \;\;\;\;\;\;\; H_{grp}^{\bullet + 1}(G,A) \xrightarrow{ \;\;\; \tau_{[g]} \;\;\; } H_{grp}^{\bullet}(C_g;\,A) \,.$$

It is a folklore theorem that the transgression (1) maps an $(n+1)$-cocycle $c \colon G^{\times_{n+1}} \to A$ to the alternating sum (of functions with values in the abelian group $A$ with group operation denoted “$+$”)

(3)$$\begin{array}{l} \tau(c) \big( \gamma, g_{n-1}, \cdots, g_1, g_0 \big) \\ \;=\; \pm \underset{ 0 \leq j \leq n }{\sum} (-1)^j \cdot c\big( g_{n-1}, \cdots,\, g_{n-j},\, Ad_j(\gamma),\, g_{n-j-1},\, \cdots,\, g_0 \big) \,, \end{array}$$

where

$$\gamma \xrightarrow{ g_{n-1} } Ad_{1}(\gamma) \xrightarrow{ g_{n-2} } \cdots \xrightarrow{\; g_0 \;} Ad_{n}(\gamma) \;\;\;\;\; \in \;\; \Lambda B G$$

is any sequence of $n$ composable morphisms in the inertia groupoid, and where we use a shorthand for the adjoint action of $G$ on itself:

$$\begin{aligned} Ad_{j}(\gamma) & \;\coloneqq\; Ad_{(g_{n-1}\cdots g_{n-j})}(\gamma) \\ & \;\coloneqq\; (g_{n-1} \cdots g_{n-j})^{-1} \cdot \gamma \cdot (g_{n-1} \cdots g_{n-j}) \,, \end{aligned}$$

(which restricts to $Ad_j(\gamma) = \gamma$ upon corestriction to the connected component on the right of (2) that is indexed by $[\gamma]$).

In historically influential examples, for the case $n = 4$ and $A = \mathbb{Z}$ or, equivalently, $n = 3$ and $A =$ U(1), this formula (3):

• implicitly underlies [Dijkgraaf & Witten 1990, p. 14] the discussion of Dijkgraaf-Witten theory;

• explains [Willerton 2008] the nature of the “twisted Drinfeld double” of the group algebra of $G$;

• governs [Dove 2019, Sec. 6.4] the expression of 4-twisted equivariant elliptic cohomology at the Tate curve in terms of 3-twisted equivariant Tate K-theory.

Below we mean to spell out a general abstract definition (Def. ) of the transgression map (1) and a full proof of its component formula (3), amplifying that its form is a direct consequence of – besides some basic homotopy theory/homological algebra which we review below – the classical Eilenberg-Zilber theorem, i.e. the Eilenberg-Zilber/Alexander-Whitney deformation retraction (which was partially re-discovered in Willerton 2008, Sec. 1 under the name “Parmesan theorem”).

Background and Lemmata

Homotopy and homological algebra

Some relevant basics of homotopy theory in relation to homological algebra:

Definition

(homotopy categories)

We write:

• $Ho(sSet)$ for the classical homotopy category, realized as the homotopy category of the classical model structure on simplicial sets;

• $Ho(sAb)$ for the homotopy category of the model structure on simplicial abelian groups;

• $Ho(Ch_+)$ for the homotopy category of the model structure on connective chain complexes.

For $A \in$ Ab, and $n \in \mathbb{N}$ we write

$$A[n] \,\in\, Ch_+ \xrightarrow{Loc_{\mathrm{W}}} Ho(Ch_+)$$

for the chain complex concentrated on $A$ in degree $n$.

We denote (using the same symbols for derived functors as for the original functors):

• the derived adjunction of the (free simplicial abelian group $\dashv$ underlying simplicial set)-Quillen adjunction (here) by

  (4)$$Ho(sAb) \underoverset {\underset{undrlg}{\longrightarrow}} {\overset{\mathbb{Z}(-)}{\longleftarrow}} {\;\;\;\;\;\;\bot\;\;\;\;\;\;} Ho(sSet)$$

• the derived adjoint equivalence of the Dold-Kan Quillen equivalence (here) by

  (5)$$Ho(Ch_+) \underoverset {\underset{DK}{\longrightarrow}} {\overset{N_\bullet}{\longleftarrow}} {\;\;\;\;\;\;\bot_{\mathrlap{\simeq}}\;\;\;\;\;\;} Ho(sAb)$$

• the derived internal-hom-Quillen adjunction (here), for any $X \in$ SimplicialSets, by

  (6)$$Ho(sSet) \underoverset {\underset{[X,-]}{\longrightarrow}} {\overset{X \times (-)}{\longleftarrow}} {\;\;\;\;\;\;\bot\;\;\;\;\;\;} Ho(sSet) \,,$$

  (whose underived right adjoint is the simplicial mapping complex-construction);

• the derived internal-hom-Quillen adjunction (here) for $\mathbb{Z}[1] \,\in\,$ ConnectiveChainComplexes:

  (7)$$Ho(Ch_+) \underoverset {\underset{ V_\bullet \mapsto V_{\bullet + 1} }{\longrightarrow}} {\overset{ V_\bullet \mapsto V_{\bullet - 1} }{\longleftarrow}} {\;\;\;\;\;\;\bot\;\;\;\;\;\;} Ho(Ch_+)$$

Simplicial classifying spaces

Remark

(delooping groupoid and simplicial classifying space of finite group)
The nerve of the delooping groupoid of a discrete group $G$ is isomorphic to the simplicial classifying space of $G$ (see this Example):

$$N \big( G \rightrightarrows \ast \big) \;\simeq\; \overline{W} G \;\;\; \in \; sSet \,.$$

For notational brevity we will be referring to $\overline{W}G$ in the following, but it may be helpful to keep thinking of this isomorphically as the nerve of the delooping groupoid, $\overline{W} G \,=\, N (G \rightrightarrows \ast)$. From this perspective, an n-simplex in $\overline{W}G$, which is an n-tuple of group elements, is suggestively denoted as a sequence of morphisms:

$$\big(\overline{W}G\big)_{n} \;\; = \;\; \Big\{ \bullet \xrightarrow{g_{n-1}} \bullet \xrightarrow{\phantom{--}} \cdots \bullet \xrightarrow{\phantom{--}} \bullet \xrightarrow{\; g_1 \;} \bullet \xrightarrow{\; g_0 \;} \bullet \;\big\vert\; g_i \in G \Big\} \,.$$

We denote the image of $\overline{W}G$ in the classical homotopy category by:

$$B G \;=\; \mathbf{B} G \;=\; Loc_{\mathrm{W}} \big( \overline{W}G \big) \;\;\; \in \; Ho(sSet)$$

(where the first equality reflects that $G$ is assumed to be discrete).

Group(oid) cohomology

Some relevant basics of cohomology, for the cases of ordinary cohomology and group cohomology:

Definition

(Eilenberg-MacLane spaces)
For $A \,\in\,$ Ab, and $n \in \mathbb{N}$, we write

$$B^n A \,=\, K(A,n) \,\coloneqq\, underlg \circ DK(A[n]) \;\;\; \in \; sAb \xrightarrow{ Loc_{\mathrm{W}}} Ho(sAb) \xrightarrow{undrlg} Ho(sSet)$$

for (the homotopy type of) the Eilenberg-MacLane space with $A$ in degree $n$ – here constructed as the underlying simplicial set of the simplicial abelian group which is the image under the Dold-Kan construction of the chain complex that is concentrated on $A$ in degree $n$.

Definition

(ordinary cohomology)
For $X \in Ho(sSet)$, $A \,\in\, Ab$ and $n \in \mathbb{N}$, the degree-$n$ ordinary cohomology of $X$ with coefficients in $A$ is the following hom-set in the classical homotopy category:

$$H^n(X;\, A) \;=\; Ho(sSet) \big( X, \, B^n A \big) \,,$$

where on the right we have the Eilenberg-MacLane space from Def. .

The following is an immediate re-casting of the traditional definition of group cohomology:

Definition

(group cohomology)
For $G \,\in\,$ Groups and $A \,\in\,$ AbelianGroups, the group cohomology of $G$ with coefficients in $A$ is, in degree $n \in \mathbb{N}$, the hom-group

$$H^n_{grp}(G;\,A) \;=\; Ho(Ch_+) \big( N_\bullet \circ \mathbb{Z}(\overline{W}G), \, A[n] \big) \,.$$

Proposition

(group cohomology is ordinary cohomology of classifying space)
For $G \,\in\,$ Groups and $A \,\in\,$ AbelianGroups, the group cohomology (Def. ) of $G$ with coefficient in $A$ is naturally isomorphic to the ordinary cohomology of the simplicial classifying space of $G$ with coefficients in $B^n A$:

$$H^n_{grp}(G;\, A) \;\simeq\; H^n(B G;\, A) \,.$$

Proof

By the hom-isomorphisms of the above derived adjunctions:

$$\begin{aligned} H^n_{grp}(G;\, A) & \;0\; Ho(Ch_+) \big( N_\bullet \circ \mathbb{Z}(\overline{W}G), \, A[n] \big) \\ & \;\simeq\; Ho(sAb) \big( \mathbb{Z}(\overline{W}G) ,\, DK(A[n]) \big) \\ & \;\simeq\; Ho(sSet) \big( \overline{W}G ,\, undrlng \circ DK(A[n]) \big) \\ & \;=\; Ho(sSet) \big( B G ,\, B^n A \big) \\ & \;=\; H^n(B G;\, A) \,. \end{aligned}$$

This Prop. , in view of Rem. justifies the following definition:

Definition

(groupoid cohomology)
For $\mathcal{G} \,=\, (\mathcal{G}_1 \rightrightarrows \mathcal{G}_0) \,\in\,$ Groupoids and $A \,\in\,$ Ab, $n \,\in\, \mathbb{N}$, the degree-$n$ groupoid cohomology of $\mathcal{G}$ with coefficients in $A$ is the ordinary cohomology (Def. ) of the homotopy type of the nerve of $\mathcal{G}$, regarded in the classical homotopy category:

$$H^n \big( \mathcal{G};\, A \big) \;\coloneqq\; Ho(sSet) \big( N(\mathcal{G}), \, B^n A \big) \,.$$

Products of simplices

Some basic facts about products of simplicial sets:

Proposition

(non-degenerate $(p+q)$-simplices in $\Delta[p] \times \Delta[q]$)
For $p,q \,\in\, \mathbb{N}$ the non-degenerate simplices in the Cartesian product (Prop. )

$$\Delta[p] \times \Delta[q]$$

of standard simplices in sSet correspond, under the Yoneda lemma, to precisely those morphisms of simplicial sets

(8)$$\Delta[p+q] \xrightarrow{\;\; \sigma \;\;} \Delta[p] \times \Delta[q]$$

which satisfy the following equivalent conditions:

• as morphisms of posets, they are strictly monotone;

• as permutations of $(p+q)$ elements they are $(p,q)$-shuffles;

• as morphisms of finitely generated categories they take generating morphisms to generating morphisms;

Such morphisms may hence be represented by paths:

• on a $(p+1)\times(q+1)$-lattice,

• from one corner to its opposite corner,

• consisting of $p+q$ unit steps,

• each either horizontally or vertially:

Proof

From this Prop. it is clear (see this Remark) that a simplex $\sigma \,\colon\, \Delta[p+q] \xrightarrow{\;} \Delta[p] \times \Delta[q]$ is degenerate precisely if, when regarded as a path as above, it contains a constant step, i.e. one which moves neither horizontally nor vertically. But then — by degree reasons, since we are looking at paths of $p + q$ steps in a lattice of side length $p$ and $q$ — it must be that the path proceeds by $p + q$ unit steps.

Nerve of the inertia groupoid

Some basic facts about the nerve of an inertia groupoid:

Proposition

(inertia groupoid of delooping groupoid is adjoint action groupoid)
The inertia groupoid $\Lambda \mathbf{B} G$ is isomorphic to the action groupoid of the adjoint action of $G$ on itself:

$$\Lambda \mathbf{B}G \;\simeq\; G_{ad} \sslash G \;=\; \left( G \times G \underoverset {Ad_{(-)}(-)} {pr_2} {\rightrightarrows} G \right)$$

This follows by immediate inspection. For more discussion see at free loop space of a classifying space the section Examples – For finite groups.

Remark

The groupoid convolution algebra of the inertia groupoid of the delooping groupoid $\mathbf{B}G$ is the Drinfeld double (see there for more) of the group algebra of $G$.

Definition

(minimal simplicial circle)
Write

$$S \;\coloneqq\; \Delta[1]/\partial\Delta[1] \;\;\; \in \; sSet$$

for the simplicial set with exactly two non-degenerate cells,

• one of which in degree 0, which we denote by $[0] = [1]$,

• and one in degree 1, which we denote by $\big[ [0], [1] \big]$.

Proposition

(normalized chain complex of minimal simplicial circle)
The normalized chain complex of the free simplicial abelian group of the minimal simplicial circle $S$ (Def. ) has the group of integers in degrees 0 and 1, and all differentials are zero:

$$N_\bullet \circ \mathbb{Z}(S) \;\simeq\; \left[ \array{ \vdots \\ \big\downarrow \\ 0 \\ \big\downarrow \\ \mathbb{Z} \\ \big\downarrow\mathrlap{ \scriptsize{0} } \\ \mathbb{Z} } \;\; \right] \;\simeq\; \mathbb{Z}[1] \,\oplus\, \mathbb{Z} \,.$$

The following proposition holds on general grounds (duscussed at free loop space of classifying space), but the explicit component-based proof we give now is necessary, further below, in order to understand the transgression-formula for cocycles in the group cohomology of $G$ to cocycles on the inertia groupoid.

Proposition

The nerve of the inertia groupoid of a delooping groupoid of a finite group $G$ is isomorphic to the simplicial hom complex out of the minimal simplicial circle $S$ (Def. ) into the simplicial classifying space $\overline{W}G$ (Rem. ):

$$N\big( \Lambda \mathbf{B}G\big)_\bullet \;\simeq\; [S,\overline{W}G]_\bullet \,.$$

Proof

This is a specialization of the general fact that the simplicial nerve repects mapping objects (see this Prop. at nerve). We spell it out for the present case:

We claim that the isomorphism is given by sending, for each $n \in \mathbb{N}$, any n-simplex $(\gamma;\, g_{n-1}, \cdots, g_1, g_0)$ of $N\big( Func( \mathbf{B}\mathbb{Z}, \, \mathbf{B}G )\big)$, being a sequence of natural transformations of the form

$$\array{ \bullet &\xrightarrow{g_{n-1}}& \bullet &\xrightarrow{g_{n-2}}& \cdots &\xrightarrow{g_{n-j-1}}& \bullet &\xrightarrow{g_{n-j-2}}& \bullet &\xrightarrow{g_{n-j-3}}& \cdots &\xrightarrow{g_{0}}& \bullet \\ \big\downarrow {}^{\mathrlap{ \gamma }} && \big\downarrow {}^{\mathrlap{ g_{n-1}^{-1} \cdot \gamma \cdot g_{n-1} }} && && \big\downarrow && \big\downarrow && && \big\downarrow\mathrlap{^{ ( g_{n-1} \cdots g_{0} )^{-1} \cdot \gamma \cdot ( g_{n-1} \cdots g_{0} ) }} \\ \bullet &\xrightarrow{g_{n-1}}& \bullet &\xrightarrow{g_{n-2}}& \cdots &\xrightarrow{g_{n-j-1}}& \bullet &\xrightarrow{g_{n-j-2}}& \bullet &\xrightarrow{g_{n-j-3}}& \cdots &\xrightarrow{g_{0}}& \bullet \mathrlap{\,,} }$$

to the homomorphism of simplicial sets

$$\Delta[n] \times S \xrightarrow{\;\;} \overline{W}G \,,$$

which, in turn, sends a non-degenerate $(n+1)$-simplex in $\Delta[n] \times S$ of the form (in the path notation discussed at product of simplices)

$$\array{ (0,[0]) &\to& (1,[0]) &\to& \cdots &\to& (j,[0]) \\ && && && \big\downarrow \\ && && && (j,[1]) &\to& (j+1,[1]) &\to& \cdots &\to& (n,[1]) }$$

to the $n+1$-simplex in $\overline{W}G$ (Rem. ) of the form

$$\array{ \bullet &\xrightarrow{g_{n-1}}& \bullet &\xrightarrow{g_{n-2}}& \cdots &\xrightarrow{g_{n-j}}& \bullet \\ && && && \big\downarrow {}^{\mathrlap{ ( g_{n-1} \cdots g_{n-j} )^{-1} \cdot \gamma \cdot ( g_{n-1} \cdots g_{n-j} ) }} \\ && && && \bullet &\xrightarrow{g_{n-j}}& \bullet &\xrightarrow{g_{n-j-1}}& \cdots &\xrightarrow{g_{0}}& \bullet }$$

As a consequence:

Proposition

The evaluation map

$$[S,\overline{W}G] \times S \xrightarrow{\;\;} \overline{W}G$$

(out of the product of the simplicial hom complex out of $S$ with $S$) maps non-degenerate $n+1$-simpleces of $[S,\overline{W}G] \times S$ as follows:

Proof

This follows by unwinding the component formula for the evaluation map on simplicial mapping complexes (this Prop.):

Recall that we denote by

(9)$$\big( \gamma ;\, g_{n-1} ,\, g_{n-2} ,\, \cdots ,\, g_{0} \big) \;\; \in \;\; \mathrm{Hom} \big( S \times \Delta[n] ,\, \overline{W}G \big) \;\simeq\; \Big( N \mathrm{Map} \big( { \mathbf{B}\mathbb{Z} } ,\, { \mathbf{B}G } \big) \Big)_{n}$$

the $n$-cell in the nerve of the inertia groupoid that corresponds to the sequence of natural transformation which start at the functor

$$\gamma \,\in\, G \,\simeq\, \mathrm{Hom}_{\mathrm{Grp}}(\mathbb{Z}, G) \,\simeq\, \mathrm{Hom}\big( \mathbf{B}\mathbb{Z} ,\, \mathbf{B}G \big)$$

and successively have components $g_{n-\bullet} \in G$.

Throughout we are writing “$Hom$” for hom-sets and “$Map$” for hom-objects, i.e. for internal homs and we keep tacitly going back and forth through the bijections in (9).

If we abbreviate (this follows conventions familiar in discussion of transgression in group cohomology)

$$\begin{aligned} Ad_{k}(\gamma) & \;\coloneqq\; Ad_{(g_{n-1}\cdots g_{n-k})}(\gamma) \\ & \;\coloneqq\; (g_{n-1} \cdots g_{n-k})^{-1} \cdot \gamma \cdot (g_{n-1} \cdots g_{n-k}) \,, \end{aligned}$$

then this corresponds to a sequence of composable morphisms in the inertia groupoid of this form:

$$\gamma \xrightarrow{ g_{n-1} } Ad_{1}(\gamma) \xrightarrow{ g_{n-2} } \cdots \xrightarrow{\; g_0 \;} Ad_{n}(\gamma) \;\;\;\;\; \in \;\; \Lambda B G$$

The simplicial map (9) maps the non-degenerate $(n+1)$-cells in the product of simplicial sets (see the discussion there) of $S$ (?) with the simplicial $n$-simplex as follows:

This is not exactly what we need unwinding the evaluation map, but it is close: the image of (9) under the $k$th degeneracy map evidently gives the following mapping:

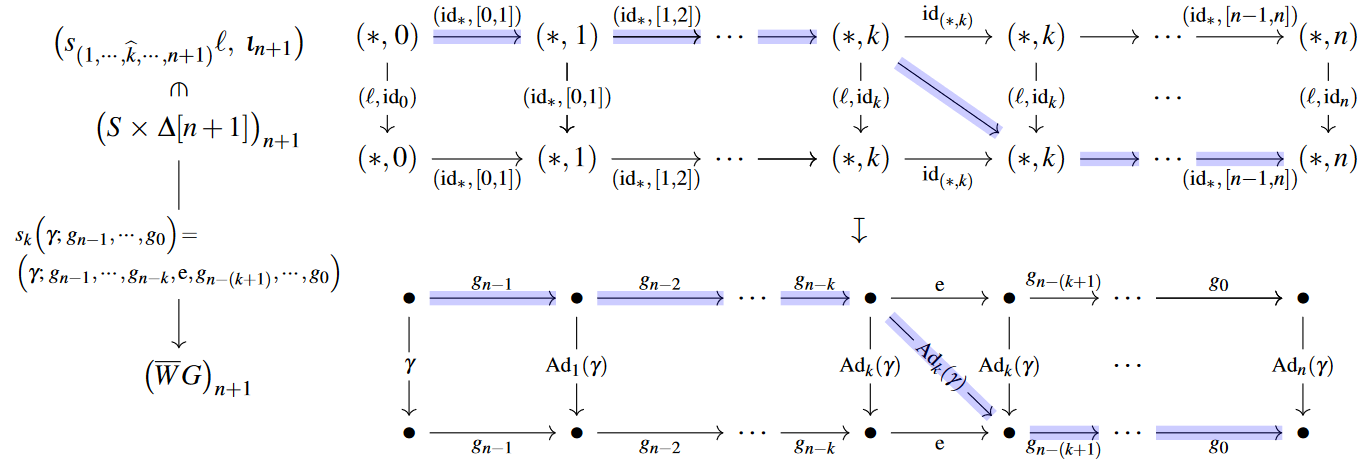
This is the type of mapping that appears in the component formula for the evaluation map on function complexes (from that Prop.), and so the claim follows.

Transgression in cohomology

Definition

(transgression) For $\mathcal{A} \,\in\, sAb$ a simplicial abelian group, hence with free loop space of its classifying space given (via this Prop.) by

(10)$$\Lambda \mathbf{B}\mathcal{A} \;\simeq\; \mathcal{A} \times \mathbf{B}\mathcal{A}$$

we say that transgression in $\mathcal{A}$-cohomology is

$$H \big( -;\, \mathbf{B}\mathcal{A} \big) \xrightarrow{ [S, -] } H \big( \Lambda(-);\, \mathcal{A} \times \mathbf{B}\mathcal{A} \big) \xrightarrow{\;\; pr_2 \;\; } H \big( \Lambda(-);\, \mathcal{A} \big) \,.$$

Proposition

(free loop space of classifying space identified via Eilenberg-Zilber map)
For $n \in \mathbb{N}_+$ and for $A \,\in\, Ab$ the integers or the circle group, the following composite of is a simplicial weak equivalence

(11)$$\begin{aligned} & \big[ S, \, B^n A \big]_\bullet \\ & \;=\; \big[ S, \, undrlng \circ DK(A[n]) \big]_\bullet \\ & \;\simeq\; sSet \big( S \times \Delta[\bullet], \, undrlng \circ DK(A[n]) \big) \\ & \;\simeq\; Ch_+ \big( N \circ \mathbb{Z}(S \times \Delta[\bullet]), \, A[n] \big) \\ & \;\xrightarrow{EZ_S}\; Ch_+ \big( N \circ \mathbb{Z}(S) \,\otimes\, N \circ \mathbb{Z}(\Delta[\bullet]), \, A[n] \big) \\ & \;\simeq\; Ch_+ \big( N \circ \mathbb{Z}(\Delta[\bullet]), \, [ N \circ \mathbb{Z}(S), \, A[n] ] \big) \\ & \;\simeq\; \Big( undrlng \circ DK \big( [ \underset{ \mathbb{Z} \oplus \mathbb{Z}[1] }{ \underbrace{ N \circ \mathbb{Z}(S) } }, \, A[n] ] \big) \Big)_\bullet \\ & \;\simeq\; \Big( undrlng \circ DK \big( A[n] \oplus A[n-1] \big) \Big)_\bullet \;=\; B^n A \times B^{n-1} A \end{aligned}$$

Here all isomorphisms are hom-isomorphisms of the above adjunctions, the step denoted $EZ_S$ is pre-composition with the Eilenberg-Zilber map, and under the brace we are using Prop. .

Proof

By the fact that the Eilenberg-Zilber map has a left inverse given by the Alexander-Whitney map $AW$ (see at Eilenberg-Zilber/Alexander-Whitney deformation retraction), the analogous composite with $AW_S$ instead of $EZ_S$ yields a left inverse morphism, which hence retracts the homotopy groups of $B^n A \times B^{n-1}A$ onto those of $\big[S, B^n A \big]$. But, by (10), the latter is a product of Eilenberg-MacLane spaces with homotopy groups $A$ concentrated in degrees $n$ and $n -1$. By assumption on $A$ the only retractions of $A$ onto itself is the identity, so that $EZ_S$ must induce the identity morphism of homotopy groups.

Proof of the component formula

We prove that the formula (3) indeed expresses transgression in group cohomology.

Proof

Consider the following sequence of natural isomorphisms of hom-sets of the above homotopy categories (Def. ):

(12)$$\begin{aligned} H^n_{grp} \big( G;\, A \big) & \;=\; Ho(sSet) \big( N_\bullet \circ \mathbb{Z}(\overline{W}G), \, A[n] \big) \\ & \;\simeq\; Ho(sSet) \big( \overline{W}G, \, undrlng \circ DK\big( A[n] \big) \big) \\ = H^n \big( B G;\, A \big) & \;\overset{[S,-]}{\to}\; Ho(sSet) \Big( [S,\overline{W}G],\, \, \big[S, undrlng \circ DK\big( A[n] \big)\big] \Big) \\ & \;\simeq\; Ho(sSet) \Big( [S,\overline{W}G] \times S, \, undrlng \circ DK\big( A[n] \big) \Big) \\ & \;\simeq\; Ho(sAbGrp) \Big( \mathbb{Z}\big( [S, \overline{W}G] \times S \big), \, DK\big(A[n]\big) \Big) \\ & \;\simeq\; Ho(Ch_+) \Big( N_\bullet \circ \mathbb{Z}\big( [S, \overline{W}G] \times S \big), \, A[n] \Big) \\ & \;\overset{EZ}{\simeq}\; Ho(Ch_+) \Big( N_\bullet \circ \mathbb{Z}\big([S, \overline{W}G]\big) \otimes \underset{ \mathbb{Z}[1] \oplus \mathbb{Z} }{ \underbrace{N_\bullet \circ \mathbb{Z}(S)} }, \, A[n] \Big) \\ & \;\simeq\; Ho(Ch_+) \Big( N_\bullet \circ \mathbb{Z}\big([S, \overline{W}G]\big), \, A[n] \oplus A[n-1] \Big) \\ & \;\overset{pr_2}{\to}\; Ho(Ch_+) \Big( N_\bullet \circ \mathbb{Z}\big([S, \overline{W}G]\big), \, A[n-1] \Big) \\ & \;=\; H^{n-1} \big( \Lambda B G; \, A \big) \,. \end{aligned}$$

Here

• the first three lines recall the identification from Prop. ;

• the fourth line is the component function on hom-sets of the derived internal hom/simplicial mapping complex-functor out of the minimal simplicial circle $S$ (Def. );

• the fifth line is the hom-isomorphisms of the derived free simplicial abelian group-adjunction (4);

• the sixth line is the hom-isomorphisms of the derived Dold-Kan equivalence (5);

• the seventh line is pre-composition with the Eilenberg-Zilber map, using that this is a quasi-isomorphism (and hence an isomorphism in the homotopy category on chain complexes) by the Eilenberg-Zilber theorem;

  under the brace we are using Prop. ;

• the eighth line is the hom-isomorphisms of the derived degree-shift adjunction (7)

  (observing that the tensor product of normalized chain complexes of free simplicial abelian groups is a cofibrant representative of the correct derived functor-image – using that all simplicial sets are cofibrant, that $\mathbb{Z}(-)$ and $N_\bullet$ are left Quillen functors, and that $(Ch_+, \otimes)$ is a monoidal model category (this Prop.), so that the tensor product with $\mathbb{Z} \oplus \mathbb{Z}[1]$ is the correct left derived functor);

• the ninth line is the projection onto the second direct summand;

• the last line is Def. of groupoid cohomology.

Chasing a group cocycle (Def. ) through this sequence, and using Prop. when it gets sent through the Eilenberg-Zilber map, manifestly outputs the sum formula (3) to be proven.

Hence it only remains to see that this concrete composite (12) is equal to the abstractly defined transgression map (Def. ).

This follows by Prop. . In detail, since:

1. $A[n] \in Ch_+$ is a fibrant object (like every object in the projective model structure on connective chain complexes);

2. $[S,\overline{W}G] \in sSet$ is a cofibrant objects (like every object in the classical model structure on simplicial sets);

the chain of hom-isomorphisms of derived adjunctions in (12) is covered (through the quotient by left homotopy that defines the homotopy category of a model category according to this Lemma) by “the same” chain of hom-isomorphisms of plain adjunctions. Using here that every simplicial set $X$ is the colimit over its elements $\Delta[k] \in el(X)$ (this Prop.) and that the 1-category-theoretic hom functors turn this colimit, in their first argument, into a limit (this Prop.), we find that the composite in (12) is covered by

$$\begin{aligned} & sSet \Big( \big[S, \overline{W}G \big], \, \big[S, undrlng \circ DK(A[n]) \big] \Big) \\ & \;\simeq\; sSet \Big( \underset{ \underset{ \mathclap{ {\Delta[k] \in} \atop {el\big([S,\overline{W}G]\big)} } } {\longrightarrow} }{\lim} \Delta[k], \, \big[S, undrlng \circ DK(A[n]) \big] \Big) \\ & \;\simeq\; \underset{ \underset{ \mathclap{ {\Delta[k] \in} \atop {el\big([S,\overline{W}G]\big)} } } {\longleftarrow} }{\lim} \, sSet \Big( \Delta[k], \, \big[S, undrlng \circ DK(A[n]) \big] \Big) \\ & \;\simeq\; \underset{ \underset{ \mathclap{ {\Delta[k] \in} \atop {el\big([S,\overline{W}G]\big)} } } {\longleftarrow} }{\lim} \, Ch_+ \Big( N_\bullet \circ \mathbb{Z} \big( S \times \Delta[k] \big), \, A[n] \Big) \\ & \;\xrightarrow{EZ_S}\; \underset{ \underset{ \mathclap{ {\Delta[k] \in} \atop {el\big([S,\overline{W}G]\big)} } } {\longleftarrow} }{\lim} \, Ch_+ \Big( N_\bullet \circ \mathbb{Z}(S) \,\otimes\, N_\bullet \circ \mathbb{Z}(\Delta[k]), \, A[n] \Big) \\ & \;\simeq\; \underset{ \underset{ \mathclap{ {\Delta[k] \in} \atop {el\big([S,\overline{W}G]\big)} } } {\longleftarrow} }{\lim} \, sSet \Big( \Delta[k], \, undrlng \circ DK \big( A[n] \oplus A[n-1] \big) \Big) \\ & \;\simeq\; sSet \Big( \underset{ \underset{ \mathclap{ {\Delta[k] \in} \atop {el\big([S,\overline{W}G]\big)} } } {\longrightarrow} }{\lim} \Delta[k], \, undrlng \circ DK \big( A[n] \oplus A[n-1] \big) \Big) \\ & \;\simeq\; sSet \Big( [S,\overline{W}G], \, undrlng \circ DK \big( A[n] \oplus A[n-1] \big) \Big) \,. \end{aligned}$$

This is manifestly the image under $sSet\big( [S,\overline{W}G], - \big)$ of the correct morphism (11) from Prop. .

References

The transgression map is alluded to in

• Robbert Dijkgraaf, Edward Witten, p. 14 of: Topological Gauge Theories and Group Cohomology, Commun. Math. Phys. 129 (1990) 393 (euclid:cmp/1104180750)

An indication of a proof, implicitly using ingredients of the Eilenberg-Zilber map (re-discovered under the name “Parmesan map”):

• Simon Willerton, Section 1 of: The twisted Drinfeld double of a finite group via gerbes and finite groupoids, Algebr. Geom. Topol. 8 (2008) 1419-1457 [arXiv:math/0503266, doi:10.2140/agt.2008.8.1419]

The transgression formula itself (without derivation) is also considered, in a context of twisted orbifold K-theory, in:

• Alejandro Adem, Yongbin Ruan, Bin Zhang, Section 4 of: A Stringy Product on Twisted Orbifold K-theory, Morfismos (10th Anniversary Issue), Vol. 11, No 2 (2007), 33-64. (arXiv:math/0605534, Morfismos pdf)

• Jean-Louis Tu, Ping Xu, Section 3 of: The ring structure for equivariant twisted K-theory, J. Reine Angew. Math. 635 (2009), 97–148 (arXiv:math/0604160, doi:10.1515/CRELLE.2009.077)

and specifically in the context of equivariant Tate K-theory:

• Thomas Dove, Twisted Equivariant Tate K-Theory (arXiv:1912.02374)

Generalization to Real $\mathbb{Z}/2$-equivariant cohomology (as appropriate for twists of KR-theory):

• Behrang Noohi, Matthew B. Young, Twisted loop transgression and higher Jandl gerbes over finite groupoids, Algebr. Geom. Topol. 22 (2022) 1663-1712 [arXiv:1910.01422, doi:10.2140/agt.2022.22.1663]

The above discussion and proof that transgression is essentially the internal hom out of the circle into the cocycle-as-a-functor is taken from:

• Hisham Sati, Urs Schreiber, Thm. 3.4 of: Cyclification of Orbifolds, Comm. Math. Phys. (2023)

following earlier observations in:

• Urs Schreiber, Zoran Škoda, §8.2 & §9.6.2 of: Categorified symmetries [arXiv:1004.2472]