nLab square
This entry is about squares in geometry. For squares in category theory see commutative square. For squares in ring theory, see square function. For squares in type theory, see square type.
Context
Topology
topology (point-set topology, point-free topology)
see also differential topology, algebraic topology, functional analysis and topological homotopy theory
Basic concepts
-
fiber space, space attachment
Extra stuff, structure, properties
-
Kolmogorov space, Hausdorff space, regular space, normal space
-
sequentially compact, countably compact, locally compact, sigma-compact, paracompact, countably paracompact, strongly compact
Examples
Basic statements
-
closed subspaces of compact Hausdorff spaces are equivalently compact subspaces
-
open subspaces of compact Hausdorff spaces are locally compact
-
compact spaces equivalently have converging subnet of every net
-
continuous metric space valued function on compact metric space is uniformly continuous
-
paracompact Hausdorff spaces equivalently admit subordinate partitions of unity
-
injective proper maps to locally compact spaces are equivalently the closed embeddings
-
locally compact and second-countable spaces are sigma-compact
Theorems
Analysis Theorems
Geometry
higher geometry / derived geometry
Ingredients
Concepts
-
geometric little (∞,1)-toposes
-
geometric big (∞,1)-toposes
Constructions
Examples
-
derived smooth geometry
Theorems
Contents
Idea
As a polygon the square is the regular 4-gon.
As a topological space it is the product topological space of the bounded closed interval with itself, .
Quotients
The identification of opposite sides of the square yields the cylinder and the torus.
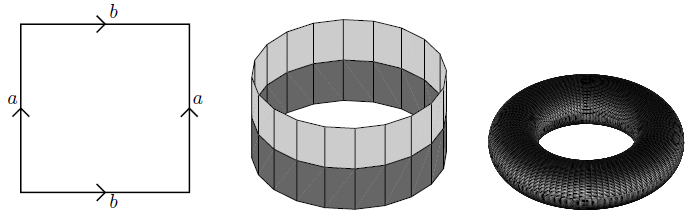
And the identification with opposite orientation yields the Möbius strip.
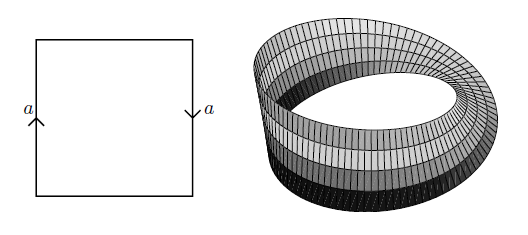
graphics grabbed from Lawson 03
Related concept
References
- Terry Lawson, Topology: A Geometric Approach, Oxford University Press (2003) (pdf)
Last revised on May 13, 2022 at 03:15:28. See the history of this page for a list of all contributions to it.