nLab single trace operator
Context
Quantum Field Theory
algebraic quantum field theory (perturbative, on curved spacetimes, homotopical)
Concepts
quantum mechanical system, quantum probability
interacting field quantization
Theorems
States and observables
Operator algebra
Local QFT
Perturbative QFT
Contents
Idea
In quantum field theory and statistical physics, a single trace operator is an observable/correlator on square matrix- or rather adjoint representation-valued scalar fields/random variables (notationally subsuming derivatives of fields) which is built from the elementary field observables as a trace over the matrix product of a finite string of them:
or more generally as linear combinations thereof.
If the fields indeed take values in the adjoint representation of a given gauge group, then the trace in the expression (1) ensures that this observable is gauge invariant. More general gauge invariant observables are hence multi-trace operators which are linear combinations of products of single-trace observables (i.e. polynomials of single-trace observables).
Properties
Correspondence to strings under AdS/CFT
Single trace operators/observables in conformal field theories such as super Yang-Mills theories play a special role in the AdS-CFT correspondence: They correspond to single string excitations on the AdS-supergravity side of the correspondence, where, curiously, the “string of characters/letters” in the argument of the trace gets literally mapped to a superstring in spacetime (see the references below).
From Polyakov 02, referring to gauge fields and their single trace operators as letter and words, respectively:
The picture which slowly arises from the above considerations is that of the space-time gradually disappearing in the regions of large curvature. The natural description in this case is provided by a gauge theory in which the basic objects are the texts formed from the gauge-invariant words. The theory provides us with the expectation values assigned to the various texts, words and sentences.
These expectation values can be calculated either from the gauge theory or from the strongly coupled 2d sigma model. The coupling in this model is proportional to the target space curvature. This target space can be interpreted as a usual continuous space-time only when the curvature is small. As we increase the coupling, this interpretation becomes more and more fuzzy and finally completely meaningless.
From Berenstein-Maldacena-Nastase 02, who write for the elementary field observables (“letters”) above:
In summary, the “string of s” becomes the physical string and that each carries one unit of which is one unit of . Locality along the worldsheet of the string comes from the fact that planar diagrams allow only contractions of neighboring operators. So the Yang Mills theory gives a string bit model where each bit is a operator.
On the CFT side these BMN operators of fixed length (of “letters”) are usefully identified as spin chains which, with the dilatation operator regarded as their Hamiltonian, are integrable systems (Minahan-Zarembo 02, Beisert-Staudacher 03).
This integrability allows a detailed matching between
-
single trace operators/BMN operators in D=4 N=4 super Yang-Mills theory
-
the classical Green-Schwarz superstring on AdS5 S5
under AdS/CFT duality (Beisert-Frolov-Staudacher-Tseytlin 03, …). For review see BBGK 04, Beisert et al. 10.
(…)
Relation to weight systems on chord diagrams
For fields valued in a Lie algebra representations of a metric Lie algebra, with a linear basis for and denoting the dual basis, those single trace operators involving only metric pairs of fields, such as
(using Einstein summation convention) are equivalently values of Lie algebra weight systems on the chord diagram that expresses the index pairing.
Such binary pairings inside the trace are induced notably after statistical averaging in the SYK model and related systems, and has been argued to appear generically for dual observables of black hole thermodynamics (Berkooz-Narayan-Simón 18, Section 2.1).
For more on this see at weight systems on chord diagrams in physics.
Examples
Shape of D D-fuzzy funnels
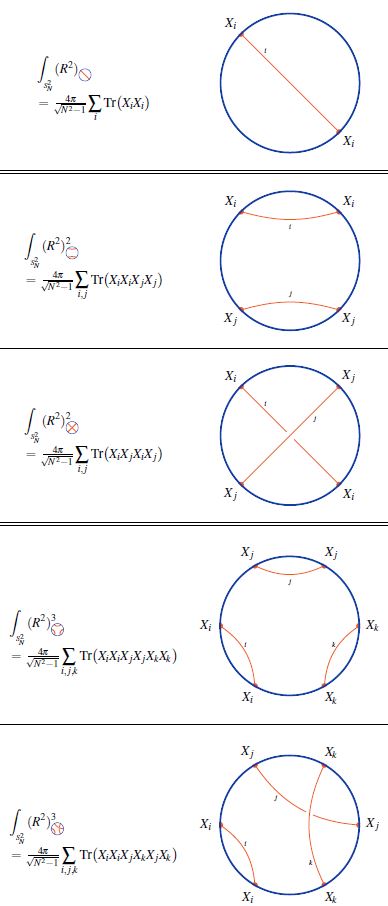
graphics from Sati-Schreiber 19c
We discuss how the single trace observables on the fuzzy 2-sphere-sections of Dp-D(p+2) brane intersection fuzzy funnels are given by su(2)-Lie algebra weight systems on chord diagrams (following Ramgoolam-Spence-Thomas 04, McNamara-Papageorgakis 05, see McNamara 06, Section 4 for review).
While in the commutative large N limit, all powers of the radius function on the fuzzy 2-sphere are equal
for finite there is an ordering ambiguity: In fact, the number of functions on the fuzzy 2-sphere at finite that all go to the same function in the large N limit grows rapidly with .
At there is the single radius observable (?)
At there are, under the integral (?), two radius observables:
(Here we are using that under the integral/trace, a cyclic permutation of the factors in the integrand does not change the result).
Similarly for higher , where the number of possible orderings increases rapidly. The combinatorics that appears here is familiar in knot theory:
Every ordering of operators, up to cyclic permutation, in the single trace observable is encoded in a chord diagram and the value of the corresponding single trace observable is the value of the su(2)-Lie algebra weight system on this chord diagram.
Related concepts
References
General
(…)
Correspondence to string excitations under AdS/CFT
The correspondence of single trace operators to superstring excitations under the AdS-CFT correspondence originates with these articles:
-
Alexander Polyakov, Gauge Fields and Space-Time, Int. J. Mod. Phys. A17S1 (2002) 119-136 (arXiv:hep-th/0110196)
-
David Berenstein, Juan Maldacena, Horatiu Nastase, Strings in flat space and pp waves from Super Yang Mills, JHEP 0204 (2002) 013 (arXiv:hep-th/0202021)
(whence “BMN operators”)
-
Steven Gubser, Igor Klebanov, Alexander Polyakov, A semi-classical limit of the gauge/string correspondence, Nucl. Phys. B636 (2002) 99-114 (arXiv:hep-th/0204051)
-
Martin Kruczenski, Spiky strings and single trace operators in gauge theories, JHEP 0508:014, 2005 (arXiv:hep-th/0410226)
The identification of the relevant single trace operators with integrable spin chains is due to
-
J. A. Minahan, Konstantin Zarembo, The Bethe-Ansatz for Super Yang-Mills, JHEP 0303 (2003) 013 (arXiv:hep-th/0212208)
-
Niklas Beisert, Matthias Staudacher, The SYM Integrable Super Spin Chain, Nucl. Phys. B 670:439-463, 2003 (arXiv:hep-th/0307042)
which led to more detailed matching of single trace operators to rotating string excitations in
- Niklas Beisert, Sergey Frolov, Matthias Staudacher, Arkady Tseytlin, Precision Spectroscopy of AdS/CFT, JHEP 0310:037, 2003 (arXiv:hep-th/0308117)
Review includes
-
A. V. Belitsky, Volker Braun, A. S. Gorsky, G. P. Korchemsky, Integrability in QCD and beyond, Int. J. Mod. Phys. A19:4715-4788, 2004 (arXiv:hep-th/0407232)
-
Niklas Beisert, Luis Alday, Radu Roiban, Sakura Schafer-Nameki, Matthias Staudacher, Alessandro Torrielli, Arkady Tseytlin, et. al., Review of AdS/CFT Integrability: An Overview, Lett. Math. Phys. 99, 3 (2012) (arXiv:1012.3982)
Relation to weight systems on chord diagrams
A general relation between single trace operators for observables on black hole thermodynamics and Lie algebra weight systems on chord diagrams (though not using the term “weight system”) is proposed in
- Micha Berkooz, Prithvi Narayan, Joan Simón, Section 2.1 of: Chord diagrams, exact correlators in spin glasses and black hole bulk reconstruction, JHEP 08 (2018) 192 (arxiv:1806.04380)
For more on this see at weight systems on chord diagrams in physics.
For JT-gravity/SYK model
Discussion of (Lie algebra-)weight systems on chord diagrams encoding SYK model single trace observables:
-
Antonio M. García-García, Yiyang Jia, Jacobus J. M. Verbaarschot, Exact moments of the Sachdev-Ye-Kitaev model up to order , JHEP 04 (2018) 146 (arXiv:1801.02696)
-
Micha Berkooz, Prithvi Narayan, Joan Simón, Chord diagrams, exact correlators in spin glasses and black hole bulk reconstruction, JHEP 08 (2018) 192 (arxiv:1806.04380)
following:
- László Erdős, Dominik Schröder, Phase Transition in the Density of States of Quantum Spin Glasses, D. Math Phys Anal Geom (2014) 17: 9164 (arXiv:1407.1552)
which in turn follows
- Philippe Flajolet, Marc Noy, Analytic Combinatorics of Chord Diagrams, pages 191–201 in Daniel Krob, Alexander A. Mikhalev,and Alexander V. Mikhalev, (eds.), Formal Power Series and Algebraic Combinatorics, Springer 2000 (doi:10.1007/978-3-662-04166-6_17)

With emphasis on holographic content:
-
Micha Berkooz, Mikhail Isachenkov, Vladimir Narovlansky, Genis Torrents, Section 5 of: Towards a full solution of the large double-scaled SYK model, JHEP 03 (2019) 079 (arxiv:1811.02584)
-
Vladimir Narovlansky, Slide 23 (of 28) of: Towards a Solution of Large Double-Scaled SYK, 2019 (pdf)
and specifically in relation to Jackiw-Teitelboim gravity:
-
Andreas Blommaert, Thomas Mertens, Henri Verschelde, The Schwarzian Theory - A Wilson Line Perspective, JHEP 1812 (2018) 022 (arXiv:1806.07765)
-
Andreas Blommaert, Thomas Mertens, Henri Verschelde, Fine Structure of Jackiw-Teitelboim Quantum Gravity, JHEP 1909 (2019) 066 (arXiv:1812.00918)
For D-D-brane intersections
Discussion of weight systems on chord diagrams as single trace observables on the fuzzy funnel/fuzzy sphere non-commutative geometry of Dp-D(p+2)-brane intersections (hence Yang-Mills monopoles):
-
Sanyaje Ramgoolam, Bill Spence, S. Thomas, Section 3.2 of: Resolving brane collapse with corrections in non-Abelian DBI, Nucl. Phys. B703 (2004) 236-276 (arxiv:hep-th/0405256)
-
Simon McNamara, Constantinos Papageorgakis, Sanyaje Ramgoolam, Bill Spence, Appendix A of: Finite effects on the collapse of fuzzy spheres, JHEP 0605:060, 2006 (arxiv:hep-th/0512145)
-
Simon McNamara, Section 4 of: Twistor Inspired Methods in Perturbative FieldTheory and Fuzzy Funnels, 2006 (spire:1351861, pdf, pdf)
-
Constantinos Papageorgakis, p. 161-162 of: On matrix D-brane dynamics and fuzzy spheres, 2006 (pdf)
Last revised on December 21, 2020 at 11:43:18. See the history of this page for a list of all contributions to it.