nLab shifted C-field flux quantization

Idea

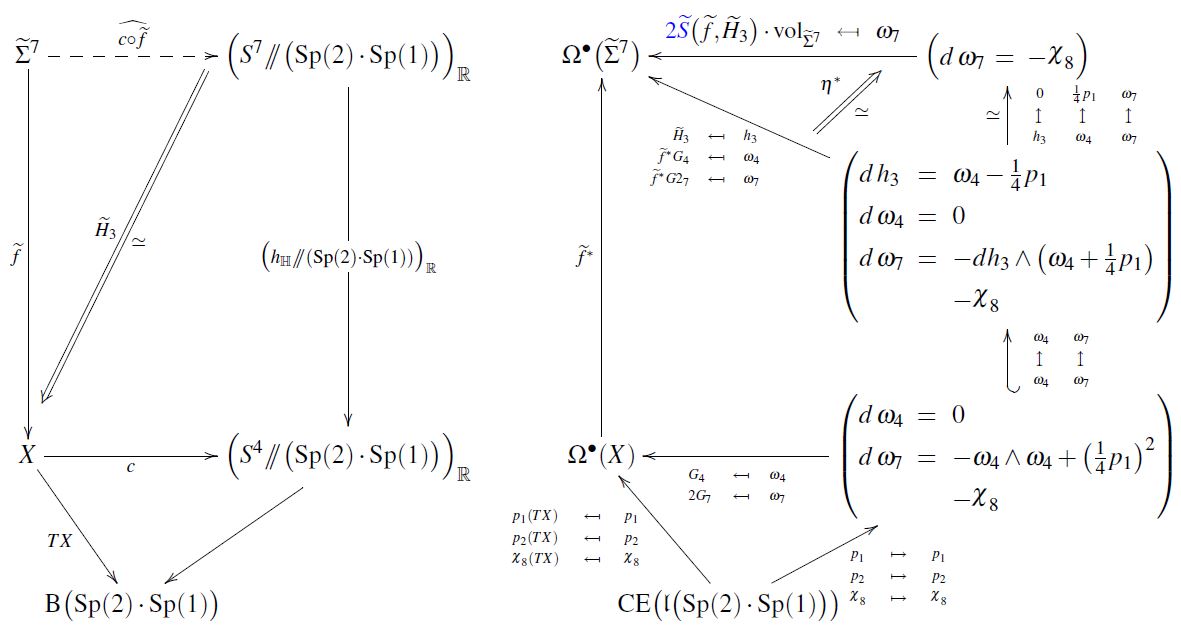
In string theory/M-theory, the shifted C-field flux quantization condition is a charge quantization-condition on the supergravity C-field expected in M-theory.

For the magnetic $G_4$-flux

For the magnetic $G_4$-flux, the shifted flux quantization says that the real cohomology class of the flux density (field strength) differential 4-form $G_4 \in \Omega^4(X)$ on spacetime $X$ becomes integral after shifted by one quarter of the first Pontryagin class, hence the condition that with the shifted 4-flux density defined as

(1)$$\widetilde G_4 \;\coloneqq\; G_4 + \tfrac{1}{4}p_1(\nabla_{T X}) \;\in\; \Omega^4(X)$$

(for $\nabla_{T X}$ any affine connection on spacetime, in particular the Levi-Civita connection) we have (using the de Rham theorem to translate from de Rham cohomology to real cohomology) that $\widetilde G_4$ represents an integral cohomology-class:

$$[\widetilde G_4] \;\in\; H^4(X, \mathbb{Z}) \overset{H^4(X, \mathbb{Z}\hookrightarrow \mathbb{R})}{\longrightarrow} H^4(X, \mathbb{R}) \,.$$

This condition was originally argued for in (Witten 96a, Witten 96b) as a sufficient condition for ensuring that the prequantum line bundle for the 7d Chern-Simons theory on an M5-brane worldvolume is divisible by 2.

Proposals for encoding this condition by a Wu class-shifted variant of stable ordinary differential cohomology were considered in Hopkins-Singer 02, Diaconescu-Freed-Moore 03, FSS 12.

It turns out that the shifted flux quantization condition on the C-field is naturally implied (FSS1 19b, Prop. 4.12) by the requirement that $G_4$ is the differential form datum underlying, via Sullivan's theorem, a cocycle in unstable J- twisted Cohomotopy in degree 4 (Hypothesis H).

For the electric $G_7$-flux

In the presence of non-vanishing C-field flux $G_4$, the electric flux density of M2-branes is not $G_7 \coloneqq \star G_4$ alone, but receives corrections, first due to the quadratic C-field self-interaction in D=11 supergravity, but then also due to the shifted C-field flux quantization expected in M-theory:

The 11d supergravity literature states the corrected 7-flux to be the following combination, also known as the Page charge (due to Page 83 (8), Duff-Stelle 91 (43), reviewed e.g. in BLMP 13, p. 21):

(2)$$\widetilde G'_7 \;\coloneqq\; G_7 + \tfrac{1}{2} C_3 \wedge G_4 \,,$$

where the second term subtracts the electric flux induced by the self-intersection of the field, and also ensures that the full expression is a closed differential form if the naive 11d supergravity equations of motion hold:

$$d \widetilde G_7 \;=\; 0 \,.$$

But in fact (2) does not quite make general sense, for two reasons:

1. In general $G_4 = 0$ is not an admissible condition and is not the actual vanshing of the C-field, due to the shifted C-field flux quantization.

2. Even if $G_4$ happens to be intregrally quantizaed (if $\tfrac{1}{4}p_1$ is integral) the appearance of a globally defined C-field potential $C_3$ in (2),means that the total flux actually does vanish after all.

Charge-quantized $\widetilde G_7$-flux with shifted C-field flux quantization (FSS 19b, Prop. 4.3, FSS 19c, Section 4)

Both of these issues are solved if the C-field is taken to be charge quantized in J-twisted Cohomotopy (Hypothesis H). This gives the corrected formula

(3)$$\widetilde G_7 \;\coloneqq\; h^\ast G_7 + \tfrac{1}{2} H_3 \wedge h^\ast \widetilde G_4$$

where

1. the expression lives on the homotopy pullback of the Sp(2)-parametrized quaternionic Hopf fibration

   $$h \coloneqq h_{\mathbb{H}}\sslash Sp(2)$$

   to spacetime, along the twisted Cohomotopy-cocycle that represents the C-field under Hypothesis H;

2. $\widetilde G_4 \coloneqq h^\ast G_4 + \tfrac{1}{4}h^\ast p_1(\nabla)$ is the integral shifted C-field pulled back to that 3-spherical fibration over spacetime;

3. $d H_3 = h^\ast G_4 - \tfrac{1}{4}h^\ast p_1(\nabla)$ trivializes not the C-field itself, but its pullback, and not absolutely but relative to the background charge implied by shifted C-field flux quantization.

With the corrected 7-flux in twisted Cohomotopy it becomes true that

1. the integral of $G_7$ around the 7-sphere linking a black M2-brane is always integer (FSS 19c, Theorem 4.6);

2. this integer satisfies the C-field tadpole cancellation condition (FSS 19b, Section 4.6).

Related concepts

• C-field tadpole cancellation

References

General

The suggestion originates in

• Edward Witten, On Flux Quantization In M-Theory And The Effective Action, J. Geom. Phys. 22:1-13, 1997 (arXiv:hep-th/9609122)

• Edward Witten, Five-Brane Effective Action In M-Theory, J. Geom. Phys. 22:103-133, 1997 (arXiv:hep-th/9610234)

Proposals to model the condition by a Wu class-shifted variant of ordinary differential cohomology include

• Michael Hopkins, Isadore Singer, Quadratic Functions in Geometry, Topology,and M-Theory J. Differential Geom. Volume 70, Number 3 (2005), 329-452. (arXiv:math.AT/0211216, euclid:1143642908)

• E. Diaconescu, Dan Freed, Greg Moore, The $M$-theory 3-form and $E_8$-gauge theory, chapter in Haynes Miller, Douglas Ravenel (eds.) Elliptic Cohomology Geometry, Applications, and Higher Chromatic Analogues, Cambridge University Press 2007 (arXiv:hep-th/0312069, doi:10.1017/CBO9780511721489)

• Dan Freed, Greg Moore, Setting the quantum integrand of M-theory, Communications in Mathematical Physics, Volume 263, Number 1, 89-132, (arXiv:hep-th/0409135, doi:10.1007/s00220-005-1482-7)

• Greg Moore, Anomalies, Gauss laws, and Page charges in M-theory, Comptes Rendus Physique 6 (2005) 251-259 (arXiv:hep-th/0409158)

• Domenico Fiorenza, Hisham Sati, Urs Schreiber, The moduli 3-stack of the C-field, Communications in Mathematical Physics, Volume 333, Issue 1 (2015), Page 117-151 (arXiv:1202.2455, doi:10.1007/s00220-014-2228-1)

Suggestion that an actual E8-principal bundle on 11d spacetime plays a role here:

• D. Diaconescu, Gregory Moore, Edward Witten, $E_8$ Gauge Theory, and a Derivation of K-Theory from M-Theory, Adv. Theor. Math. Phys. 6:1031-1134, 2003 (arXiv:hep-th/0005090)

• Diaconescu-Freed-Moore 03, Section 3

• Allan Adams, Jarah Evslin, The loop group of $E_8$ and K-theory from 11d, JHEP 02 (2003) (arXiv:hep-th/0203218)

• Hisham Sati, $E_8$ Gauge Theory and Gerbes in String Theory, Adv. Theor. Math. Phys. 14:1-39, 2010 (arXiv:hep-th/0608190)

The observation that the condition is implied by C-field charge quantization in J-twisted Cohomotopy (Hypothesis H):

• Domenico Fiorenza, Hisham Sati, Urs Schreiber, Twisted Cohomotopy implies M-theory anomaly cancellation,

  Comm. Math. Phys. 377 (2020) 1961-2025 (doi:10.1007/s00220-020-03707-2, arXiv:1904.10207)

• Domenico Fiorenza, Hisham Sati, Urs Schreiber, Twisted Cohomotopy implies M5 WZ term level quantization, Comm. Math. Phys. 384 403–432 (2021) (doi:10.1007/s00220-021-03951-0, arXiv:1906.07417)

surveyed in:

• Domenico Fiorenza, Hisham Sati, Urs Schreiber, Sec. 5.3 of: The Character Map in Twisted Non-Abelian Cohomology (arXiv:2009.11909)

Discussion of the Page charge in relation to the Myers effect in M-theory for M2-branes polarizing into M5-branes of fuzzy 3-sphere-shape:

• Krzysztof Pilch, Alexander Tyukov, Nicholas Warner, Flowing to Higher Dimensions: A New Strongly-Coupled Phase on M2 Branes, JHEP11 (2015) 170 (arXiv:1506.01045)

Relation to Freed-Witten anomaly

On relating the Freed-Witten anomaly to the shifted C-field flux quantization:

On D4-branes:

• Edward Witten, Section 2 of: Duality Relations Among Topological Effects In String Theory, JHEP 0005:031, 2000 (arXiv:hep-th/9912086)

On D6-branes:

• Sergei Gukov, James Sparks, p. 21 of: M-Theory on $Spin(7)$ Manifolds, Nucl. Phys. B625 (2002) 3-69 (arXiv:hep-th/0109025)

• James Sparks, Global Worldsheet Anomalies from M-Theory, JHEP 0408:037, 2004 (arXiv:hep-th/0310147)