nLab quantum circuit diagram
Context
Quantum systems
quantum algorithms:
Computation
constructive mathematics, realizability, computability
propositions as types, proofs as programs, computational trinitarianism
Constructive mathematics
Realizability
Computability
Monoidal categories
With braiding
With duals for objects
-
category with duals (list of them)
-
dualizable object (what they have)
-
ribbon category, a.k.a. tortile category
With duals for morphisms
-
monoidal dagger-category?
With traces
Closed structure
Special sorts of products
Semisimplicity
Morphisms
Internal monoids
Examples
Theorems
In higher category theory
Contents
Idea
Broadly a quantum logic circuit is a logic circuit but in the context of quantum information theory/quantum computation. Concretely, due to the linear logic/linear type theory underlying quantum physics:
In the context of quantum computation, a quantum circuit diagram (originally: “quantum computational network”, Deutsch 1989) is a kind of string diagram (Abramsky & Coecke 2004) in finite-dimensional Hilbert spaces, typically used to express a sequence of low-level quantum gates mapping between spaces of pure quantum states.
A generic pure quantum circuit might look as follows:
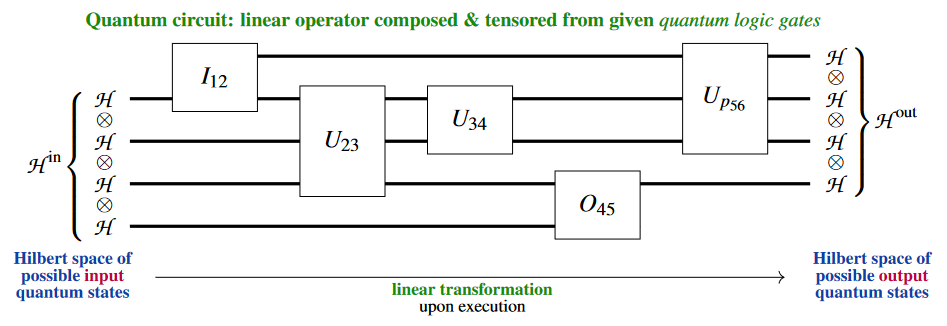
[figure from Myers et al. 2023]
Here, for instance, the “quantum gate” is a linear operator on the tensor product Hilbert space .
Notice that the quantum circuit is understood to be the actual string diagram, up to the usual admissible topological deformations, not just the composite linear transformation which it encodes: The compositeness of the diagram encodes how (e.g. in which order) available quantum gate-operations would be operated on an actual quantum computer, and the composite linear map only encodes the inpute-to-output-specification of the resulting quantum computation. In this sense, quantum circuits constitute a quantum programming language and one also speaks of the “quantum circuit model of quantum computation” (e.g. Nielsen & Chuang 2000, §II.4.6; Miszczak 2011, §3, 2012, §4.3; Beneti & Casati 2018, §3.2).
Accordingly, many existing quantum programming languages are actually domain specific programming languages for quantum circuits, and as such they are often embedded into ambient type theories (for instance Quipper and QWIRE).
Often the basic Hilbert space building block here is taken to be complex 2-dimensional, , in which case one speaks of a quantum circuit on q-bits.
Sometimes all quantum gates involved, and hence also the resulting composite linear maps, are assumed to be invertible, as befits reversible computation by unitary quantum state evolution in quantum mechanics.
But more generally and certainly in the broader context of quantum information theory (such as in formulating the quantum teleportation protocol and similar), quantum circuits are admitted to also contain crucial classical/quantum mechanics-interaction, in the form of:
-
quantum measurement-gates,
-
quantum state preparation-gates,
-
classically controlled quantum gates.
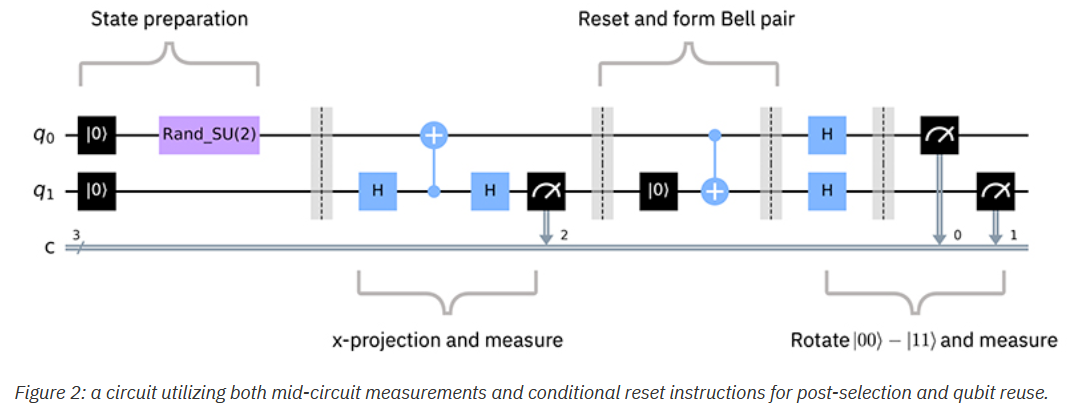
Here quantum measurement, in particular, is not only non-reversible (due to the quantum state collapse involved) but also non-deterministic, meaning that it is not immediately represented by a fixed linear map at all – at least not between the original Hilbert spaces.
One may model the -tuple of projection operators corresponding to the possible set of measurement outcomes as a linear map between the original Hilbert space and its -indexed direct sum (one rare place where this is made explicit, albeit without comment, is Selinger 2004, p. 39):
Therefore, as soon as these three operations crossing the classical/quantum physics-boundary are involved (and made explicit), quantum circuits are no longer just string diagrams in finite-dimensional HilbertSpaces, but something richer, involving besides tensor products also some kind of reflection of direct sums of spaces of quantum states.
For a critical assessment of the (lack of) literature on this issue see Gurevich & Blass 2021.
One approach for handling these more general quantum circuits is (Aharonov, Kitaev & Nisan 1998, Selinger 2004) to understand them, in the tradition on quantum probability theory, as diagrams of “quantum operations” on spaces of mixed quantum states, namely as a kind of string diagrams of completely positive maps between convex spaces of density matrices.
Other approaches for giving categorical semantics for quantum circuits in this general sense have been proposed (and implemented) in the discussion of the quantum programming language Quipper (see the references there). A natural formulation in terms of Quantum Modal Logic in terms of dependent linear type theory is discussed at:
These turn out to be related: From a suitably rich formulation of quantum circuits of pure states with measurement and classical control, the density matrix-formulation may be recovered (…).
At the time of writing (2021) most of the actual programming of experimental quantum computers is conceived through quantum circuit diagrams, while more high-level quantum programming languages are are awaiting the rise of more powerful quantum hardware.
Examples
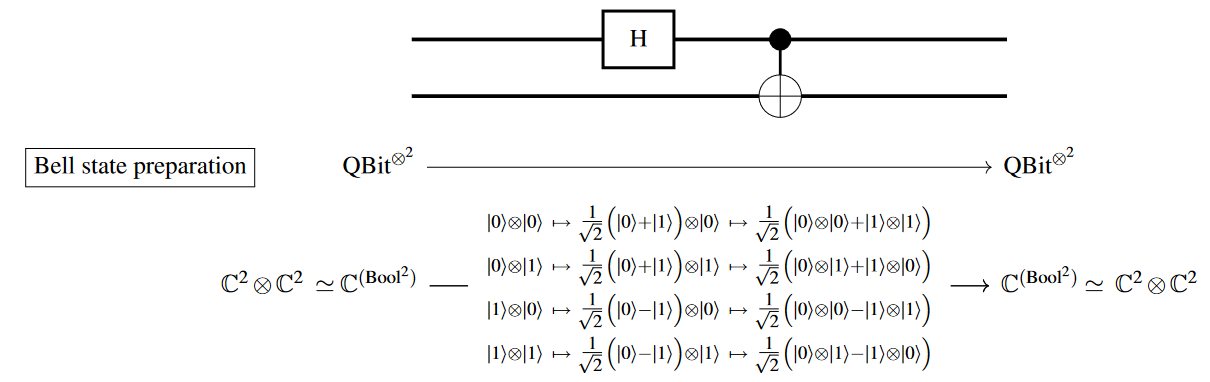
Bell state preparation
In qbit-based quantum computation, the elementary Bell state is usually prepared via the following small quantum circuit consisting of a Hadamard gate followed by a quantum CNOT gate:
Quantum teleportation
The standard (cf. GLRSV13, p. 5) qbit-form of the quantum teleportation-protocol is the following quantum ciruit on qbits (where “” denotes the Hadamard gate, the circles denote the quantum CNOT gates and the boxed pointers denote quantum measurement in the qbit-basis):

Properties
Deferred measurement principle
See at deferred measurement principle.
Related concepts
References
Quantum circuit diagrams
The notion of quantum gates and quantum circuits acting on pure quantum states originates with:
-
Richard Feynman, Quantum mechanical computers, Foundations of Physics 16 (1986) 507–531 [doi:10.1007/BF01886518]
-
David E. Deutsch, Quantum computational networks, Proceedings of the Royal Society A, 425 1868 (1989) 73-90 [doi:10.1098/rspa.1989.0099, jstor:2398494]
-
Adriano Barenco, Charles H. Bennett, Richard Cleve, David P. DiVincenzo, Norman Margolus, Peter Shor, Tycho Sleator, John A. Smolin, Harald Weinfurter, Elementary gates for quantum computation, Phys. Rev. A52 (1995) 3457 [arXiv:quant-ph/9503016, doi:10.1103/PhysRevA.52.3457]
On quantum circuits for mixed quantum states (with density matrices) and rigorous propsals for the classical/quantum interaction:
-
Dorit Aharonov, Alexei Kitaev, Noam Nisan, Quantum Circuits with Mixed States, Proceedings of the Thirtieth Annual ACM Symposium on Theory of Computation (STOC) (1998) 20-30 [arXiv:quant-ph/9806029, doi:10.1145/276698.276708]
-
Peter Selinger, Towards a quantum programming language, Mathematical Structures in Computer Science 14 4 (2004) 527–586 [doi:10.1017/S0960129504004256, pdf, web]
-
Yuri Gurevich, Andreas Blass, Quantum circuits with classical channels and the principle of deferred measurements, Theoretical Computer Science 920 (2022) 21–32 [arXiv:2107.08324, doi:10.1016/j.tcs.2022.02.002]
Standard textbook accounts:
-
Michael A. Nielsen, Isaac L. Chuang, Section II.4 in: Quantum computation and quantum information, Cambridge University Press (2000) [doi:10.1017/CBO9780511976667, pdf, pdf]
-
Jarosław Adam Miszczak, Sec. 3 of: Models of quantum computation and quantum programming languages, Bull. Pol. Acad. Sci.-Tech. Sci., 59 3 (2011)305-324 [arXiv:1012.6035, doi:10.2478/v10175-011-0039-5]
-
Jarosław Adam Miszczak, Section 4.3 in: High-level Structures for Quantum Computing, Morgan&Claypool (2012) [doi:10.2200/S00422ED1V01Y201205QMC006, pdf]
-
Quantum Circuit Model of Computation, 2015 (pdf)
-
Giuliano Benenti, Giulio Casati, Davide Rossini, Chapter 3 of: Principles of Quantum Computation and Information, World Scientific (2018) [doi:10.1142/10909, 2004 pdf]
Standard lecture notes:
-
John Preskill, Classical and quantum circuits (pdf), Chapter 5 in: Quantum Computation, lecture notes (web)
-
Ryan O’Donnell, Introduction to the Quantum Circuit Model (2015) (pdf)
-
Scott Aaronson, §4.2 in: Introduction to Quantum Information Science (2018) [pdf, webpage]
Survey of simulating and designing quantum circuits:
- Alwin Zulehner and Robert Wille: Simulation and Design of Quantum Circuits, in: Reversible Computation: Extending Horizons of Computing. RC 2020 Lecture Notes in Computer Science 12070, Springer (2020) [doi:10.1007/978-3-030-47361-7_3]
The (dagger-compact monoidal) category theoretic formulation is due to:
- Samson Abramsky, Bob Coecke, A categorical semantics of quantum protocols, Proceedings of the 19th IEEE conference on Logic in Computer Science (LiCS’04). IEEE Computer Science Press (2004) [arXiv:quant-ph/0402130, doi:10.1109/LICS.2004.1319636]
with exposition and further development in:
-
Bob Coecke, Kindergarten Quantum Mechanics, in Quantum Theory: Reconsideration of Foundations (QTRF 3) Vaxjo, Sweden, June 6-11, 2005, AIP Conf. Proc. 810 (2006) [arXiv:quant-ph/0510032, doi:10.1063/1.2158713]
-
Bob Coecke, Quantum Picturalism, Contemporary Physics 51 (2010) 59-83 [arXiv:0908.1787, doi:10.1080/00107510903257624]
For more on this see at finite quantum mechanics in terms of dagger-compact categories.
See also:
-
Wikipedia, Quantum circuit
-
Stephen P. Jordan, Sec. 1.2 in: Quantum Computation Beyond the Circuit Model (arXiv:0809.2307)
On quantum circuits as (geodesic, if optimal) computational paths:
-
Michael A. Nielsen, Mark R. Dowling, Mile Gu, Andrew C. Doherty, Quantum Computation as Geometry, Science, 311 5764 (2006) 1133-1135 [doi:10.1126/science.1121541, arXiv:quant-ph/0603161]
-
Mark R. Dowling, Michael A. Nielsen, The geometry of quantum computation, Quantum Information & Computation 8 10 (2008) 861–899 [doi:10.5555/2016985.2016986, arXiv:quant-ph/0701004]
Survey, examples, and implementations:
-
Michal Charemza, Examples of Quantum Circuit Diagrams, 2006 (pdf)
-
Qiskit, Defining Quantum Circuits
-
South Korea Qiskit Hackathon’20 - Qiskit Metal exercise
(tutorial for a 2-qbit quantum chip using Qiskit)
-
Microsof Build, Quantum circuit diagrams
-
Vladimir P. Gerdt, Alexander N. Prokopenya, The Circuit Model of Quantum Computation and Its Simulation with Mathematica, In: Adam G., Buša J., Hnatič M. (eds.) Mathematical Modeling and Computational Science MMCP 2011. Lecture Notes in Computer Science, vol 7125. Springer 2011 (doi:10.1007/978-3-642-28212-6_4)
With an eye towards quantum complexity theory:
- Richard Cleve, Section 1.2 in: An Introduction to Quantum Complexity Theory (pdf)
Formal quantum programming language-perspective on quantum circuits:
- Yuri Gurevich, Andreas Blass, Software science view on quantum circuit algorithms [arXiv:2209.13731]
See also:
- M. Amy, M. Crawford, A. N. Glaudell, M. L. Macasieb, S. S. Mendelson, Neil J. Ross, Catalytic Embeddings of Quantum Circuits [arXiv:2305.07720]
Parameterized quantum circuits
Discussion of classically-parameterized quantum circuits:
(…)
Discussion of quantumly-parameterized quantum circuits:
- Evan Peters, Prasanth Shyamsundar, Qarameterized circuits: Quantum parameters for QML [web]
following
-
Guillaume Verdon, Jason Pye, Michael Broughton, A Universal Training Algorithm for Quantum Deep Learning [arXiv:1806.09729]
-
Prasanth Shyamsundar, Non-Boolean Quantum Amplitude Amplification and Quantum Mean Estimation [arXiv:2102.04975]
Quantum information theory via String diagrams
General
The observation that a natural language for quantum information theory and quantum computation, specifically for quantum circuit diagrams, is that of string diagrams in †-compact categories (see quantum information theory via dagger-compact categories):
-
Samson Abramsky, Bob Coecke, A categorical semantics of quantum protocols, Proceedings of the 19th IEEE conference on Logic in Computer Science (LiCS’04). IEEE Computer Science Press (2004) arXiv:quant-ph/0402130, doi:10.1109/LICS.2004.1319636
-
Samson Abramsky, Bob Coecke, Abstract Physical Traces, Theory and Applications of Categories, 14 6 (2005) 111-124. [tac:14-06, arXiv:0910.3144]
-
Samson Abramsky, Bob Coecke, Categorical quantum mechanics, in Handbook of Quantum Logic and Quantum Structures, Elsevier (2008) arXiv:0808.1023, ISBN:9780080931661, doi:10.1109/LICS.2004.1319636
-
Bob Coecke, De-linearizing Linearity: Projective Quantum Axiomatics from Strong Compact Closure, Proceedings of the 3rd International Workshop on Quantum Programming Languages (2005), Electronic Notes in Theoretical Computer Science 170 (2007) 49-72 [doi:10.1016/j.entcs.2006.12.011, arXiv:quant-ph/0506134]
On the relation to quantum logic/linear logic:
-
Samson Abramsky, Ross Duncan, A Categorical Quantum Logic, Mathematical Structures in Computer Science 16 3 (2006) arXiv:quant-ph/0512114, doi:10.1017/S0960129506005275
-
Ross Duncan, Types for quantum mechanics, 2006 pdf, slides
Early exposition with introduction to monoidal category theory:
-
Bob Coecke, Kindergarten quantum mechanics arXiv:quant-ph/0510032
-
Bob Coecke, Introducing categories to the practicing physicist arXiv:0808.1032
-
John Baez, Mike Stay, Physics, topology, logic and computation: a rosetta stone in: New Structures for Physics, Bob Coecke (ed.), Lecture Notes in Physics 813, Springer (2011) 95-174 arxiv/0903.0340
-
Bob Coecke, Eric Oliver Paquette, Categories for the practising physicist, in: New Structures for Physics, Lecture Notes in Physics 813, Springer (2010) arXiv:0905.3010, doi:10.1007/978-3-642-12821-9_3
-
Bob Coecke, Quantum Picturalism, Contemporary Physics 51 1 (2010) arXiv:0908.1787, doi:10.1080/00107510903257624
Review in contrast to quantum logic:
- Samson Abramsky, Bob Coecke, Physics from Computer Science: a Position Statement, International Journal of Unconventional Computing 3 3 (2007) pdf, ijuc-3-3-p-179-197
and with emphasis on quantum computation:
- Jamie Vicary, The Topology of Quantum Algorithms, (LICS 2013) Proceedings of 28th Annual ACM/IEEE Symposium on Logic in Computer Science (2013) 93-102 arXiv:1209.3917, doi:10.1109/LICS.2013.14
Generalization to quantum operations on mixed states (completely positive maps of density matrices):
-
Peter Selinger, Dagger compact closed categories and completely positive maps, Electronic Notes in Theoretical Computer Science 170 (2007) 139-163 doi:10.1016/j.entcs.2006.12.018, web, pdf
-
Bob Coecke, Chris Heunen, Pictures of complete positivity in arbitrary dimension, Information and Computation 250 50-58 (2016) arXiv:1110.3055, doi:10.1016/j.ic.2016.02.007
-
Bob Coecke, Chris Heunen, Aleks Kissinger,
Categories of Quantum and Classical Channels, EPTCS 158 (2014) 1-14 arXiv:1408.0049, doi:10.4204/EPTCS.158.1
Textbook accounts (with background on relevant monoidal category theory):
-
Bob Coecke, Aleks Kissinger, Picturing Quantum Processes – A First Course in Quantum Theory and Diagrammatic Reasoning, Cambridge University Press (2017) ISBN:9781107104228
-
Chris Heunen, Jamie Vicary, Categories for Quantum Theory, Oxford University Press 2019 ISBN:9780198739616
based on:
Chris Heunen, Jamie Vicary, Lectures on categorical quantum mechanics (2012) pdf, pdf
-
Bob Coecke, Stefano Gogioso, Quantum in Pictures, Quantinuum Publications (2023) ISBN 978-1739214715, Quantinuum blog
(focus on ZX-calculus)
Measurement & Classical structures
Formalization of quantum measurement via Frobenius algebra-structures (“classical structures”):
-
Bob Coecke, Duško Pavlović, Quantum measurements without sums, in Louis Kauffman, Samuel Lomonaco (eds.), Mathematics of Quantum Computation and Quantum Technology, Taylor & Francis (2008) 559-596 arXiv:quant-ph/0608035, doi:10.1201/9781584889007
-
Bob Coecke, Eric Oliver Paquette, POVMs and Naimark’s theorem without sums, Electronic Notes in Theoretical Computer Science 210 (2008) 15-31 arXiv:quant-ph/0608072, doi:10.1016/j.entcs.2008.04.015
-
Bob Coecke, Eric Oliver Paquette, Duško Pavlović, Classical and quantum structuralism, in: Semantic Techniques in Quantum Computation, Cambridge University Press (2009) 29-69 arXiv:0904.1997, doi:10.1017/CBO9781139193313.003
-
Bob Coecke, Duško Pavlović, Jamie Vicary, A new description of orthogonal bases, Mathematical Structures in Computer Science 23 3 (2012) 555- 567 arXiv:0810.0812, doi:10.1017/S0960129512000047
and the evolution of the “classical structures”-monad into the “spider”-diagrams (terminology for special Frobenius normal form, originating in Coecke & Paquette 2008, p. 6, Coecke & Duncan 2008, Thm. 1) of the ZX-calculus:
-
Bob Coecke, Ross Duncan, §3 in: Interacting Quantum Observables, in Automata, Languages and Programming. ICALP 2008, Lecture Notes in Computer Science 5126, Springer (2008) doi:10.1007/978-3-540-70583-3_25
-
Aleks Kissinger, §§2 in: Graph Rewrite Systems for Classical Structures in -Symmetric Monoidal Categories, MSc thesis, Oxford (2008) pdf, pdf
-
Aleks Kissinger, §4 in: Exploring a Quantum Theory with Graph Rewriting and Computer Algebra, in: Intelligent Computer Mathematics. CICM 2009, Lecture Notes in Computer Science 5625 (2009) 90-105 doi:10.1007/978-3-642-02614-0_12
-
Bob Coecke, Ross Duncan, Def. 6.4 in: Interacting Quantum Observables: Categorical Algebra and Diagrammatics, New J. Phys. 13 (2011) 043016 arXiv:0906.4725, doi:10.1088/1367-2630/13/4/043016
ZX-Calculus
Evolution of the “classical structures”-Frobenius algebra (above) into the “spider”-ingredient of the ZX-calculus for specific control of quantum circuit-diagrams:
-
Bob Coecke, Ross Duncan, §3 in: Interacting Quantum Observables, in Automata, Languages and Programming. ICALP 2008, Lecture Notes in Computer Science 5126, Springer (2008) doi:10.1007/978-3-540-70583-3_25
-
Aleks Kissinger, Graph Rewrite Systems for Classical Structures in -Symmetric Monoidal Categories, MSc thesis, Oxford (2008) pdf, pdf
-
Aleks Kissinger, Exploring a Quantum Theory with Graph Rewriting and Computer Algebra, in: Intelligent Computer Mathematics. CICM 2009, Lecture Notes in Computer Science 5625 (2009) 90-105 doi:10.1007/978-3-642-02614-0_12
-
Bob Coecke, Ross Duncan, Interacting Quantum Observables: Categorical Algebra and Diagrammatics, New J. Phys. 13 (2011) 043016 arXiv:0906.4725, doi:10.1088/1367-2630/13/4/043016
Relating the ZX-calculus to braided fusion categories for anyon braiding:
- Fatimah Rita Ahmadi, Aleks Kissinger, Topological Quantum Computation Through the Lens of Categorical Quantum Mechanics arXiv:2211.03855
Quantum programming languages
The first proposal towards formalizing quantum programming languages was:
- Emanuel Knill, Conventions for quantum pseudocode, Los Alamos Technical Report (1996) LA-UR-96-2724, doi:10.2172/366453, pdf, pdf
and early formalization via quantum lambda-calculus invoking linear logic/linear types (cf. Pratt 1992 etc.):
-
Benoît Valiron, A functional programming language for quantum computation with classical control, MSc thesis, University of Ottawa (2004) doi:10.20381/ruor-18372, pdf
-
Peter Selinger, Benoît Valiron, A lambda calculus for quantum computation with classical control, Proc. of TLCA 2005 arXiv:cs/0404056, doi:10.1007/11417170_26
-
Peter Selinger, Benoît Valiron, Quantum Lambda Calculus, in: Semantic Techniques in Quantum Computation, Cambridge University Press (2009) 135-172 doi:10.1017/CBO9781139193313.005, pdf
[Selinger (2016):] When the QPL workshop series was first founded, it was called “Quantum Programming Languages”. One year I wasn’t participating, and while I wasn’t looking they changed the name to “Quantum Physics and Logic” — same acronym!
Back in those days in the early 21st century we were actually trying to do programming languages for quantum computing Selinger & Valiron 2004, but the sad thing is: In those days nobody really cared.
Now it’s 15 years later and several of these parameters have changed: There has been a renewed interest, from government agencies and also from companies who are actually building quantum computers. .
So now people are working on quantum programming languages again.
Exposition of the general idea of quantum programming languages for classically controlled quantum computation with an eye towards the Quipper-language:
- Benoît Valiron, Neil J. Ross, Peter Selinger, D. Scott Alexander, Jonathan M. Smith, Programming the quantum future, Communications of the ACM 58 8 (2015) 52–61 doi:10.1145/2699415, pdf, web, promo vid:YT
On quantum programming languages (programming languages for quantum computation):
General:
-
Jarosław Adam Miszczak, Models of quantum computation and quantum programming languages, Bull. Pol. Acad. Sci.-Tech. Sci., Vol. 59, No. 3 (2011), pp. 305-324 (arXiv:1012.6035)
-
Jarosław Adam Miszczak, High-level Structures for Quantum Computing, Morgan&Claypool 2012 (doi:10.2200/S00422ED1V01Y201205QMC006, pdf)
See also:
- Wikipedia, Quantum programming
Surveys of existing languages:
-
Simon Gay, Quantum programming languages: Survey and bibliography, Mathematical Structures in Computer Science16(2006) (doi:10.1017/S0960129506005378, pdf)
-
Sunita Garhwal, Maryam Ghorani , Amir Ahmad, Quantum Programming Language: A Systematic Review of Research Topic and Top Cited Languages, Arch Computat Methods Eng 28, 289–310 (2021) (doi:10.1007/s11831-019-09372-6)
-
B. Heim et al., Quantum programming languages, Nat Rev Phys 2 (2020) 709–722 doi:10.1038/s42254-020-00245-7
Quantum programming via quantum logic understood as linear type theory interpreted in symmetric monoidal categories:
-
Vaughan Pratt, Linear logic for generalized quantum mechanics, in Proc. of Workshop on Physics and Computation (PhysComp’92), Dallas (1992) pdf, Pratt-LinearLogic.pdf, web
-
Samson Abramsky, Bob Coecke, A categorical semantics of quantum protocols , Proceedings of the 19th IEEE conference on Logic in Computer Science (LiCS’04). IEEE Computer Science Press (2004) (arXiv:quant-ph/0402130)
-
Samson Abramsky, Ross Duncan, A Categorical Quantum Logic, Mathematical Structures in Computer Science, 16 3 (2006) 469-489 arXiv:quant-ph/0512114, doi:10.1017/S0960129506005275
-
Ross Duncan, Types for Quantum Computing, (2006) pdf
-
Ugo Dal Lago, Claudia Faggian, On Multiplicative Linear Logic, Modality and Quantum Circuits, EPTCS 95 (2012) 55-66 arXiv:1210.0613, doi:10.4204/EPTCS.95.6
-
Sam Staton, Algebraic Effects, Linearity, and Quantum Programming Languages, POPL ‘15: Proceedings of the 42nd Annual ACM SIGPLAN-SIGACT Symposium on Principles of Programming Languages (2015) doi:10.1145/2676726.2676999, pdf
“A quantum programming language captures the ideas of quantum computation in a linear type theory.”
The corresponding string diagrams are known in quantum computation as quantum circuit diagrams:
-
Giuliano Benenti, Giulio Casati, Davide Rossini, Chapter 3 of: Principles of Quantum Computation and Information, World Scientific 2018 (doi:10.1142/10909, 2004 pdf)
Typedfunctional programming languages for quantum computation:
QPL:
- Peter Selinger, Towards a quantum programming language, Mathematical Structures in Computer Science 14 4 (2004) 527–586 doi:10.1017/S0960129504004256, pdf, web
QML:
-
Thorsten Altenkirch, Jonathan Grattage, A functional quantum programming language, Logic in Computer Science, 2005. Proceedings. 20th Annual IEEE Symposium on, 26-29 June 2005 Page(s):249 - 258 (arXiv:quant-ph/0409065, doi:10.1109/LICS.2005.1, pdf)
-
Jonathan Grattage, An overview of QML with a concrete implementation in Haskell, talk at Quantum Physics and Logic 2008, ENTCS: Proceedings of QPL V - DCV IV, 157-165, Reykjavik, Iceland, 2008 (arXiv:0806.2735)
- Thorsten Altenkirch, Alexander Green, The quantum IO monad, Ch. 5 of: Simon Gay, Ian Mackie (eds.): Semantic Techniques in Quantum Computation (2010) 173-205 pdf, doi:10.1017/CBO9781139193313.006
-
Peter Selinger, The Quipper Language (web)
-
Alexander Green, Peter LeFanu Lumsdaine, Neil Ross, Peter Selinger, Benoît Valiron, Quipper: A Scalable Quantum Programming Language, ACM SIGPLAN Notices 48 6 (2013) 333-342 arXiv:1304.3390
-
Alexander Green, Peter LeFanu Lumsdaine, Neil Ross, Peter Selinger, Benoît Valiron, An Introduction to Quantum Programming in Quipper, Lecture Notes in Computer Science 7948:110-124, Springer, 2013 (arXiv:1304.5485)
-
Jonathan Smith, Neil Ross, Peter Selinger, Benoît Valiron, Quipper: Concrete Resource Estimation in Quantum Algorithms, QAPL 2014 (arXiv:1412.0625)
-
Francisco Rios, Peter Selinger, A Categorical Model for a Quantum Circuit Description Language, EPTCS 266, 2018, pp. 164-178 (arXiv:1706.02630)
-
Jennifer Paykin, Robert Rand, Steve Zdancewic, QWIRE: a core language for quantum circuits, POPL 2017: Proceedings of the 44th ACM SIGPLAN Symposium on Principles of Programming Languages (2017) 846–858 (doi:10.1145/3009837.3009894)
(using the exponential modality between linear type theory and intuitionistic type theory)
-
Jennifer Paykin, Linear/non-Linear Types For Embedded Domain-Specific Languages, 2018 (upenn:2752)
-
Jennifer Paykin, Steve Zdancewic, A HoTT Quantum Equational Theory, talk at QPL2019 arXiv:1904.04371, talk slides: pdf, pdf
(using ambient homotopy type theory)
CoqQ:
- Li Zhou, Gilles Barthe, Pierre-Yves Strub, Junyi Liu, Mingsheng Ying, CoqQ: Foundational Verification of Quantum Programs arXiv:2207.11350
On Q Sharp:
- Kartik Singhal, Kesha Hietala, Sarah Marshall, Robert Rand, Q# as a Quantum Algorithmic Language, Proceedings of Quantum Physics and Logic (2022) arXiv:2206.03532
On classically controlled quantum computation:
- Bernhard Ömer, Structured Quantum Programming, 2003/2009 (pdf)
Quantum programming via dependent linear type theory/indexed monoidal (∞,1)-categories:
-
Urs Schreiber, Quantization via Linear Homotopy Types (arXiv:1402.7041)
-
Peng Fu, Kohei Kishida, Peter Selinger, Linear Dependent Type Theory for Quantum Programming Languages, LICS ‘20: Proceedings of the 35th Annual ACM/IEEE Symposium on Logic in Computer ScienceJuly 2020 Pages 440–453 (arXiv:2004.13472, doi:10.1145/3373718.3394765, pdf, video)
specifically with Quipper:
- Peng Fu, Kohei Kishida, Neil Ross, Peter Selinger, A Tutorial Introduction to Quantum Circuit Programming in Dependently Typed Proto-Quipper, in I. Lanese, M. Rawski (eds.) Reversible Computation RC 2020. Lecture Notes in Computer Science, vol 12227 (arXiv:2005.08396, doi:10.1007/978-3-030-52482-1_9)
See also QS.
On quantum software engineering:
- Manuel A. Serrano, Ricardo Pérez-Castillo, Mario Piattini, Quantum Software Engineering, Springer (2022) doi:10.1007/978-3-031-05324-5
with QWIRE:
-
Robert Rand, Jennifer Paykin, Steve Zdancewic, QWIRE Practice: Formal Verification of Quantum Circuits in Coq, EPTCS 266, 2018, pp. 119-132 (arXiv:1803.00699)
-
Robert Rand, Jennifer Paykin, Dong-Ho Lee, Steve Zdancewic, ReQWIRE: Reasoning about Reversible Quantum Circuits, EPTCS 287 (2019) 299-312 arXiv:1901.10118, doi:10.4204/EPTCS.287.17
- Linda Anticoli, Carla Piazza, Leonardo Taglialegne, Paolo Zuliani, Towards Quantum Programs Verification: From Quipper Circuits to QPMC, In: Devitt S., Lanese I. (eds.) Reversible Computation. RC 2016, Lecture Notes in Computer Science 9720 Springer (2016) arXiv:1708.06312, doi:10.1007/978-3-319-40578-0_16
with CoqQ: Ying et al. (2022)
Last revised on February 5, 2024 at 08:08:42. See the history of this page for a list of all contributions to it.