nLab orientifold plane
Context
String theory
Ingredients
Critical string models
Extended objects
Topological strings
Backgrounds
Phenomenology
Contents
Idea
In type II string theory on orientifolds (Dai-Leigh-Polchinski 89), one says O-plane for the fixed point locus of the -involution (see at real space).
O-planes carry D-brane charges in KR-theory (Witten 98), see (DMR 13) for a mathematical account. They serve RR-field tadpole cancellation and as such play a key role in the construction of intersecting D-brane models for string phenomenology.
Properties
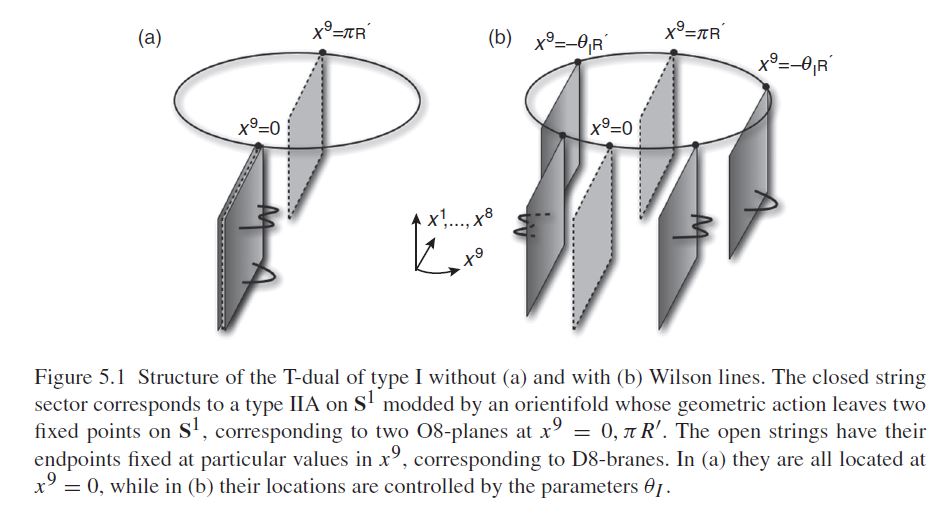
T-Duality with type I string theory
Under T-duality, type I string theory is dual to type II string theory with orientifold planes (reviewed e.g. in Ibanez-Uranga 12, section 5.3.2 - 5.3.4):
O-Plane charge
O-planes carry effective negative RR-charge which may (must) cancel against the actual RR- D-brane charge via RR-field tadpole cancellation.
For flat orientifolds
The charge of the spacetime-filling -plane of plain type I string theory (type II string theory on the orientifold with trival spacetime -action) is found by worldsheet-computation to be in units of D9-brane charge:
(e.g. Blumenhagen-Lüst-Theisen 13 (9.83)).
Remark
counting of D-branes on orientifolds
Beware that there is some convention involved in assigning an absolute value of unit D-brane charge . A common choice in the literature is to mean by “one D-brane” one of the two pre-images on the covering space, in which case its obsolute charge is to be
(e.g. BDHKMMS 01, p. 46-47). From BLT 13, p. 318:

This means that RR-field tadpole cancellation here requires the presence of 32 D-branes (or rather, by Remark : 16 and their -mirror images), hence a space-filling D9-brane with Chan-Paton bundle of rank , corresponding to a gauge group SO(32). For more on this see at type I string theory – Tadpole cancellation and SO(32)-GUT.
From this the O-brane charge for follows from T-duality (as above) with respect to KK-compactification on a d-torus with -action given by canonical coordinate reflection
This results in -planes with worldvolume . But since the orbifold now has singularities /fixed points (this Example) there are now such -planes.
Since the number of D-branes does not change under T-duality, the total O-plane charge should be the same as before
which means that the -plane charge is
or equivalently
(e.g. Ibáñez-Uranga 12 (5.52), Blumenhagen-Lüst-Theisen 13 (10.212))
In summary, we have the following table of O-plane charges on flat orbifolds:
| O-plane species | charge | transverse d-torus | fixed points |
|---|---|---|---|
In particular the O4-plane has negative unit charge (in units of D4-brane charge ), so that the total charge of here comes entirely from the number of fixed points of the -action on .
O-plane charges of different dimension may be present
graphics grabbed from Johnson 97
In the presence of discrete torsion
In the presence of discrete torsion in the B-field and/or the RR-fields, this charge structure of orientifold planes on flat orbifolds gets further modified (Hanany-Kol 00, Sec. 2.1, see Bergman-Gimon-Sugimoto 01, Sec. 1):
graphics grabbed from Bergman-Gimon-Sugimoto 01
(In comparing this last table with the above table, notice that this shows the Op-plane charge in units of as in (2).)
In differential equivariant KR-theory
A proposal for a formalization of a much more general formula for O-plane charge, regarded in differential equivariant KR-theory is briefly in Distler-Freed-Moore 09, p. 6.
Duality with M-Theory
The possible O-planes in M-theory are (M-wave), MO5 (M5-brane) and MO9 (Hanany-Kol 00 around (3.2), HSS 18, Prop. 4.7).
Under the duality between M-theory and type IIA string theory the O8-plane is identified with the MO9 of Horava-Witten theory:
graphics grabbed from GKSTY 02, section 3
while the O4-plane is dual to the MO5 (Hori 98, Gimon 98, Sec. III, AKY 98, Sec. II B, Hanany-Kol 00, 3.1.1)
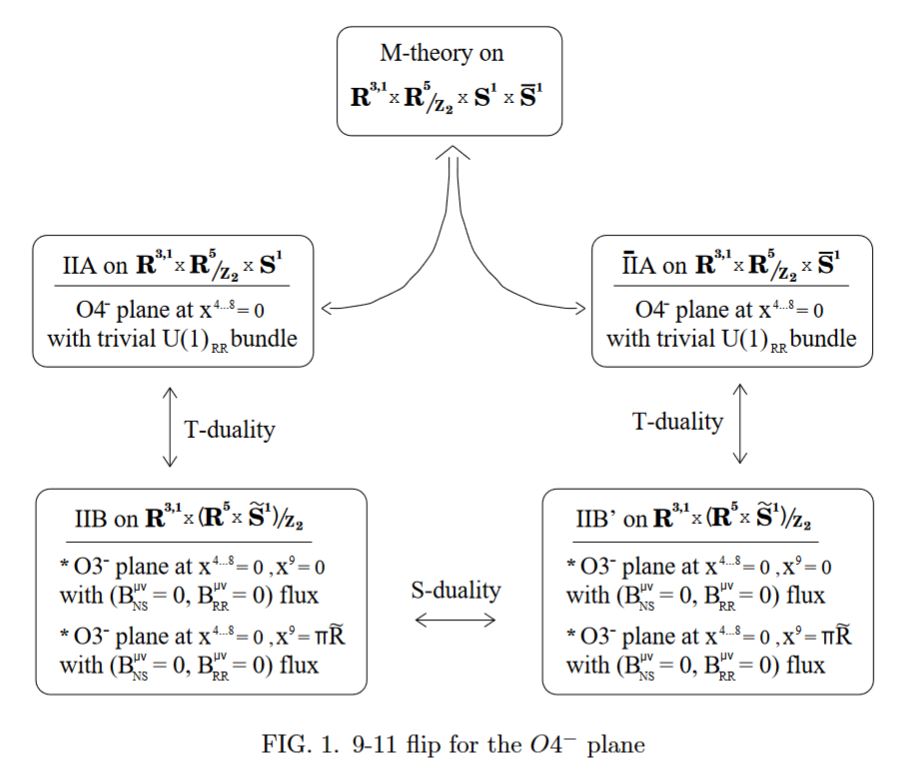
graphics grabbed from Gimon 98
and the to the MO1 (Hanany-Kol 00 3.3)
Fractional branes at O-planes
By the discussion at D-branes ending on NS5 branes, a black D6-brane may end on a black NS5-brane, and in fact a priori each brane NS5-brane has to be the junction of two black D6-branes.
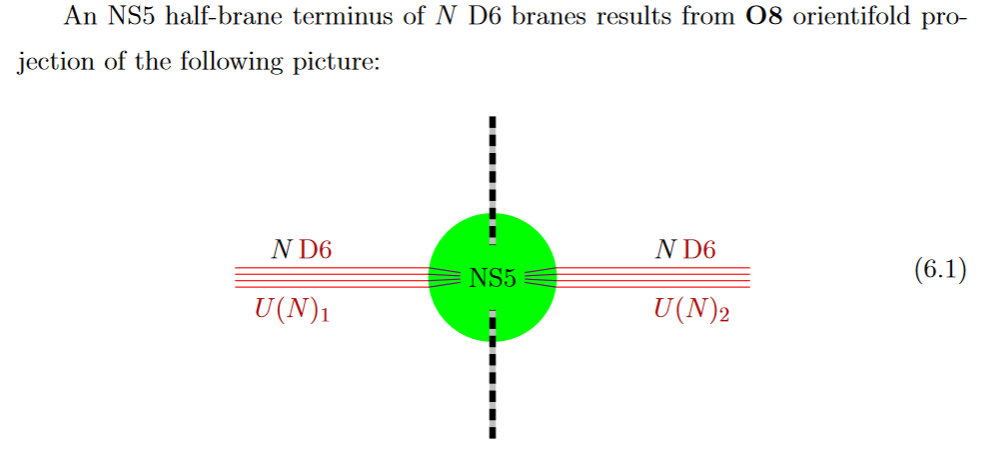
from GKSTY 02
If in addition the black NS5-brane sits at an O8-plane, hence at the orientifold fixed point-locus, then in the ordinary -quotient it appears as a “half-brane” with only one copy of D6-branes ending on it:
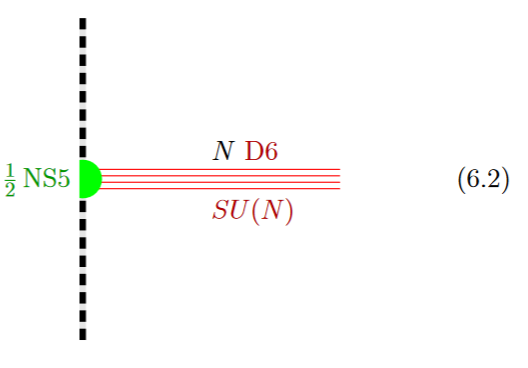
from GKSTY 02
(In Hanany-Zaffaroni 99 this is interpreted in terms of the 't Hooft-Polyakov monopole.)
The lift to M-theory of this situation is an M5-brane intersecting an M9-brane:
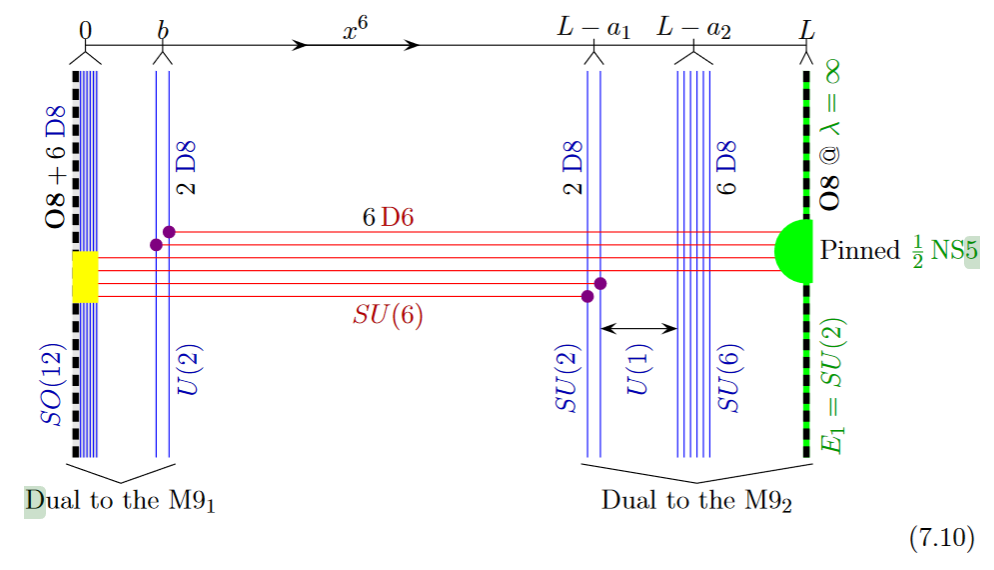
from GKSTY 02
Alternatively the O8-plane may intersect the black D6-branes away from the black NS5-brane:
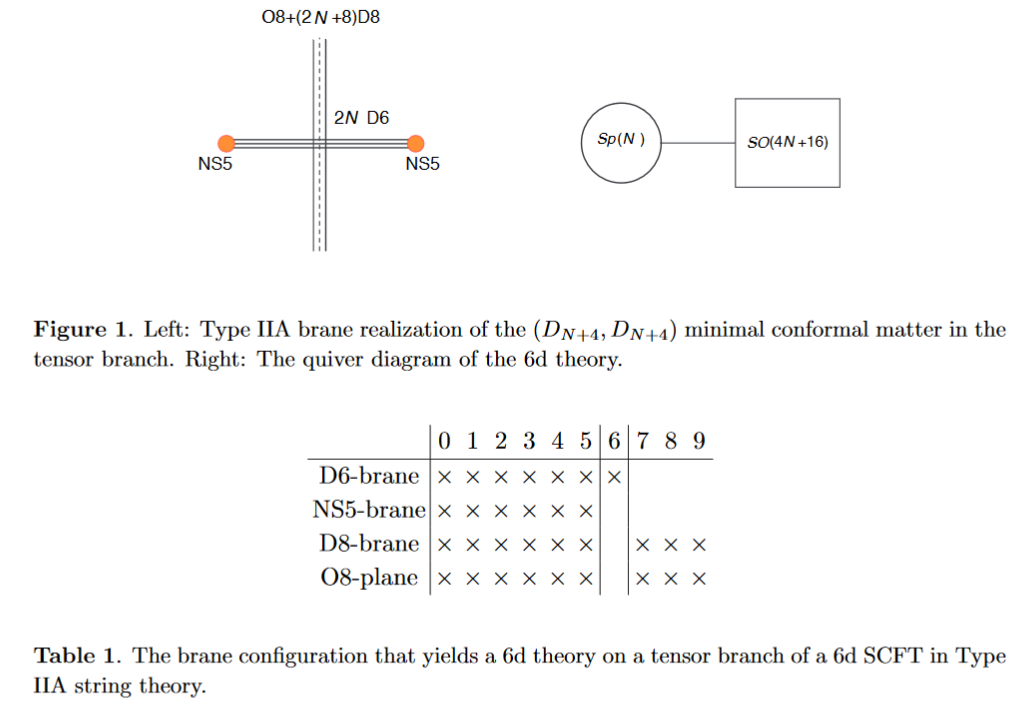
from HKLY 15
In general, some of the NS5 sit away from the O8-plane, while some sit on top of it:
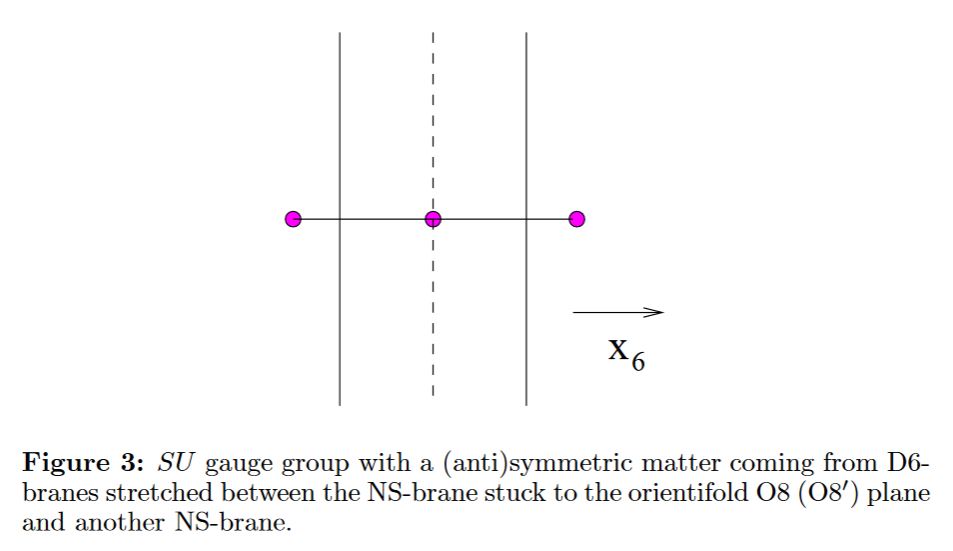
from Hanany-Zaffaroni 98
See also at intersecting D-brane models the section Intersection of D6s with O8s.
Related concepts
References
General
The term “orientifold” originates around
- Jin Dai, R.G. Leigh, Joseph Polchinski, p. 12 of New Connections Between String Theories, Mod.Phys.Lett. A4 (1989) 2073-2083 (spire:25758)
Other early accounts include
-
Clifford Johnson, Anatomy of a Duality, Nucl.Phys. B521 (1998) 71-116 (arXiv:hep-th/9711082)
-
Amihay Hanany, Alberto Zaffaroni, Branes and Six Dimensional Supersymmetric Theories, Nucl.Phys. B529 (1998) 180-206 (arXiv:hep-th/9712145)
-
Edward Witten, section 5 of D-branes and K-theory, J. High Energy Phys., 1998(12):019, 1998 (arXiv:hep-th/9810188)
-
Sunil Mukhi, Nemani V. Suryanarayana, Gravitational Couplings, Orientifolds and M-Planes, JHEP 9909 (1999) 017 (arXiv:hep-th/9907215)
-
Yoshifumi Hyakutake, Yosuke Imamura, Shigeki Sugimoto, Orientifold Planes, Type I Wilson Lines and Non-BPS D-branes, JHEP 0008 (2000) 043 (arXiv:hep-th/0007012)
-
Jan de Boer, Robbert Dijkgraaf, Kentaro Hori, Arjan Keurentjes, John Morgan, David Morrison, Savdeep Sethi, section 3 of Triples, Fluxes, and Strings, Adv.Theor.Math.Phys. 4 (2002) 995-1186 (arXiv:hep-th/0103170)
Textbook accounts:
-
Luis Ibáñez, Angel Uranga, section 10 of String Theory and Particle Physics – An Introduction to String Phenomenology, Cambridge 2012
-
Ralph Blumenhagen, Dieter Lüst, Stefan Theisen, Section 9.4 and 10.6 of Basic Concepts of String Theory Part of the series Theoretical and Mathematical Physics, Springer 2013
See also
- Wikipedia, Orientifold
With discrete torsion
O-Plane charge in the presence of discrete torsion:
-
Oren Bergman, Eric Gimon, Shigeki Sugimoto, Orientifolds, RR Torsion, and K-theory, JHEP 0105:047, 2001 (arXiv:hep-th/0103183)
-
Atish Dabholkar, Jaemo Park, Strings on Orientifolds, Nucl. Phys. B477 (1996) 701-714 (arXiv:hep-th/9604178)
In terms of KO-theory
O-Plane charge in differential equivariant KR-theory:
-
Charles Doran, Stefan Mendez-Diez, Jonathan Rosenberg, T-duality For Orientifolds and Twisted KR-theory (arXiv:1306.1779)
-
Jacques Distler, Dan Freed, Greg Moore, Orientifold Précis in: Hisham Sati, Urs Schreiber (eds.) Mathematical Foundations of Quantum Field and Perturbative String Theory Proceedings of Symposia in Pure Mathematics, AMS (2011) (arXiv:0906.0795, slides)
-
Jacques Distler, Dan Freed, Greg Moore, Spin structures and superstrings (arXiv:1007.4581)
reviewed/surveyed in
-
Daniel Freed, Dirac charge quantiation, K-theory, and orientifolds, talk at a workshop Mathematical methods in general relativity and quantum field theories, Paris, November 2009 (pdf, pdf)
-
Greg Moore, The RR-charge of an orientifold, Oberwolfach talk 2010 (pdf, pdf, ppt)
-
Daniel Freed, Lectures on twisted K-theory and orientifolds, lecures at K-Theory and Quantum Fields, ESI 2012 (pdf)
Actual construction of twisted differential orthogonal K-theory and its relation to D-brane charge in type I string theory (on orientifolds):
- Daniel Grady, Hisham Sati, Twisted differential KO-theory (arXiv:1905.09085)
Examples / Models
The Witten-Sakai-Sugimoto model for QCD on O-planes:
- Toshiya Imoto, Tadakatsu Sakai, Shigeki Sugimoto, and QCD from String Theory, Prog.Theor.Phys.122:1433-1453, 2010 (arXiv:0907.2968)
Lift to M-theory
-
Kentaro Hori, Consistency Conditions for Fivebrane in M Theory on Orbifold, Nucl.Phys.B539:35-78, 1999 (arXiv:hep-th/9805141)
-
Eric Gimon, On the M-theory Interpretation of Orientifold Planes (arXiv:hep-th/9806226, spire:472499)
-
Changhyun Ahn, Hoil Kim, Hyun Seok Yang, SCFT and M Theory on , Phys.Rev. D59 (1999) 106002 (arXiv:hep-th/9808182)
-
E. Gorbatov, V.S. Kaplunovsky, J. Sonnenschein, Stefan Theisen, S. Yankielowicz, section 3 of On Heterotic Orbifolds, M Theory and Type I’ Brane Engineering, JHEP 0205:015, 2002 (arXiv:hep-th/0108135)
-
Amihay Hanany, Barak Kol, On Orientifolds, Discrete Torsion, Branes and M Theory, JHEP 0006 (2000) 013 (arXiv:hep-th/0003025)
-
Hirotaka Hayashi, Sung-Soo Kim, Kimyeong Lee, Futoshi Yagi, 6d SCFTs, 5d Dualities and Tao Web Diagrams (arXiv:1509.03300)
-
John Huerta, Hisham Sati, Urs Schreiber, Real ADE-equivariant (co)homotopy and Super M-branes (arXiv:1805.05987)
The intersection with (p,q)5-brane webs:
-
Hirotaka Hayashi, Sung-Soo Kim, Kimyeong Lee, Masato Taki, Futoshi Yagi, More on 5d descriptions of 6d SCFTs, JHEP10 (2016) 126 (arXiv:1512.08239)
-
Amihay Hanany, Alberto Zaffaroni, Issues on Orientifolds: On the brane construction of gauge theories with global symmetry, JHEP 9907 (1999) 009 (arXiv:hep-th/9903242)
-
Gabi Zafrir, Brane webs in the presence of an -plane and 4d class S theories of type D, JHEP07 (2016) 035 (arXiv:1602.00130)
Last revised on November 1, 2023 at 12:10:22. See the history of this page for a list of all contributions to it.