nLab multi-trace operator
Context
Quantum Field Theory
algebraic quantum field theory (perturbative, on curved spacetimes, homotopical)
Concepts
quantum mechanical system, quantum probability
interacting field quantization
Theorems
States and observables
Operator algebra
Local QFT
Perturbative QFT
Contents
Idea
A multi trace observable in a gauge theory is a polynomial in single trace operators (see there for more background).
Properties
Under AdS/CFT correspondence
Under the AdS/CFT correspondence, single trace observables in the gauge theory correspond to single particle/string excitations on the gravity-side, while multi-trace observables correspond to multi-particle/string excitations (Liu 98, p. 6 (7 of 39), Andrianapoli-Ferrara 99, p. 13, Chalmers-Schalm 00, Section 7, Aharony-Gubser-Maldacena-Ooguri-Oz 99, p. 75)
The asymptotic boundary conditions for fields on the AdS-side
that correspond to multi-trace observables have coefficients given by the derivative of the multi-trace polynomial by its single-trace variables :
Examples
Chord diagrams as multi-trace observables in the BMN matrix model
The supersymmetric states of the BMN matrix model are temporally constant complex matrices which are complex metric Lie representations of su(2) (interpreted as fuzzy 2-sphere noncommutative geometries of giant gravitons or equivalently as fuzzy funnels of D0-D2 brane bound states).
A fuzzy 2-sphere-rotation invariant multi-trace observable on these supersymmetric states is hence an expression of the following form:
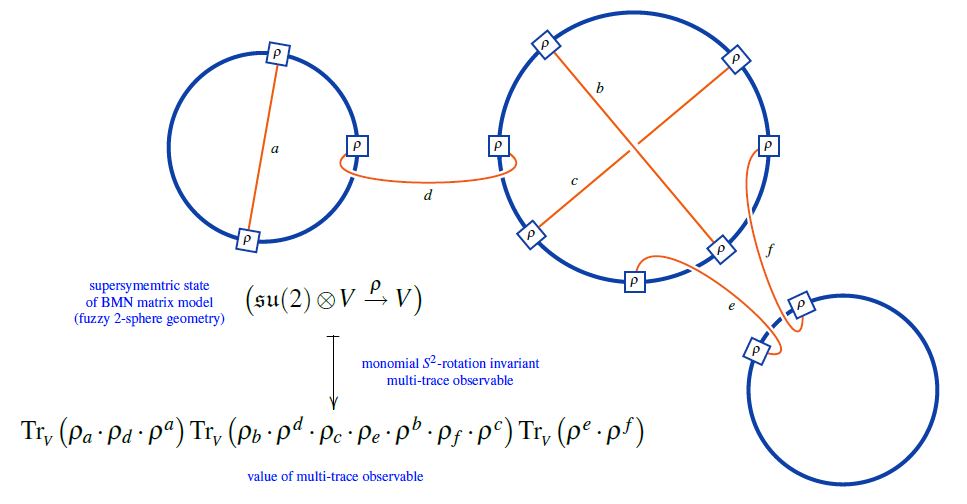
(from Sati-Schreiber 19c)
Here we are showing the corresponding string diagram/Penrose notation for metric Lie representations, which makes manifest that
-
these multi-trace observables are encoded by Sullivan chord diagrams
-
their value on the supersymmetric states is the evaluation of the corresponding Lie algebra weight system on .
Or equivalently, if is a horizontal chord diagram whose -permuted closure is (see here) then the values of the invariant multi-trace observables on the supersymmetric states of the BMN matrix model are the evaluation of on , as shown here:
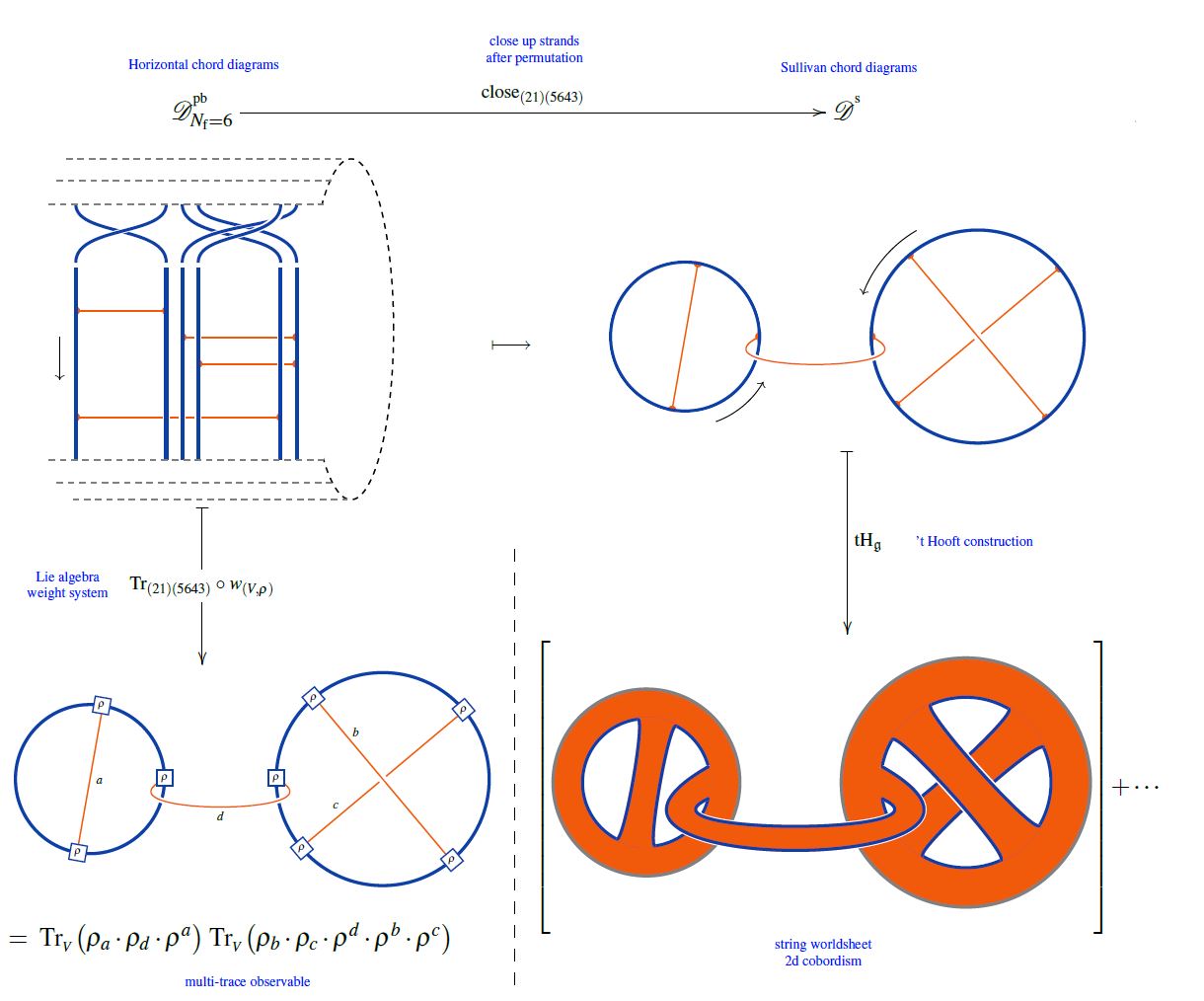
(from Sati-Schreiber 19c)
But since all horizontal weight systems are partitioned Lie algebra weight systems this way, this identifies supersymmetric states of the BMN matrix model as seen by invariant multi-trace observables as horizontal chord diagrams evaluated in Lie algebra weight systems.
References
Discussion of multi-trace operators in super Yang-Mills theory and of their AdS-CFT dual gravity/string theory incarnation:
-
Tom Banks, Michael Douglas, Gary Horowitz, Emil Martinec, AdS Dynamics from Conformal Field Theory (arXiv:hep-th/9808016, spire:474214)
-
Hong Liu, Scattering in Anti-de Sitter Space and Operator Product Expansion, Phys. Rev. D 60, 106005 (1999) (arXiv:hep-th/9811152)
-
Laura Andrianopoli, Sergio Ferrara, On short and long multiplets in the AdS/CFT correspondence, Lett. Math.Phys. 48 (1999) 145-161 (arXiv:hep-th/9812067)
-
Gordon Chalmers, Koenraad Schalm, Holographic Normal Ordering and Multi-particle States in the AdS/CFT Correspondence, Phys. Rev. D61:046001, 2000 (arXiv:hep-th/9901144)
-
Ofer Aharony, Steven Gubser, Juan Maldacena, Hirosi Ooguri, Yaron Oz, Large Field Theories, String Theory and Gravity, Phys. Rept. 323:183-386, 2000 (arXiv:hep-th/9905111)
-
Massimo Bianchi, Stefano Kovacs, Giancarlo Rossi, Yassen S. Stanev, On the logarithmic behaviour in SYM theory, JHEP 9908 (1999) 020 (arXiv:hep-th/9906188)
-
Witold Skiba, Correlators of Short Multi-Trace Operators in Supersymmetric Yang-Mills, Phys. Rev. D 60, 105038 (1999) (arXiv:hep-th/9907088)
-
Eric D'Hoker, Daniel Freedman, Samir Mathur, A. Matusis, Leonardo Rastelli, Extremal Correlators in the AdS/CFT Correspondence, in: The many faces of the superworld (arXiv:hep-th/9908160)
-
Gleb Arutyunov, Sergey Frolov, A. C. Petkou, Perturbative and instanton corrections to the OPE of CPOs in , Nucl. Phys. B602:238-260, 2001; Erratum-ibid. B609:540, 2001 (arXiv:hep-th/0010137)
-
Ofer Aharony, Micha Berkooz, Eva Silverstein, Multiple-Trace Operators and Non-Local String Theories, JHEP 0108:006, 2001 (arXiv:hep-th/0105309)
-
Ofer Aharony, Micha Berkooz, Eva Silverstein, Non-local string theories on times and stable non-supersymmetric backgrounds, Phys. Rev. D65:106007, 2002 (arXiv:hep-th/0112178)
-
L. Hoffmann, L. Mesref, A. Meziane, W. Rühl, Multi-trace quasi-primary fields of from AdS -point functions, Nucl. Phys. B641 (2002) 188-222 (arXiv:hep-th/0112191)
-
Edward Witten, Multi-Trace Operators, Boundary Conditions, And AdS/CFT Correspondence (arXiv:hep-th/0112258)
-
Steven Gubser, Indrajit Mitra, Double-trace operators and one-loop vacuum energy in AdS/CFT, Phys. Rev. D67 (2003) 064018 (arXiv:hep-th/0210093)
-
Vijay Balasubramanian, Jan de Boer, Bo Feng, Yang-Hui He, Min-xin Huang, Vishnu Jejjala, Asad Naqvi, Multi-Trace Superpotentials vs. Matrix Models, Commun. Math. Phys. 242:361-392, 2003 (arXiv:hep-th/0212082)
-
Steven Gubser, Igor Klebanov, A universal result on central charges in the presence of double-trace deformations, Nucl. Phys. B656 (2003) 23-36 (arXiv:hep-th/0212138)
-
P. J. Heslop, Paul Howe, Aspects of =4 SYM, JHEP 0401 (2004) 058 (arXiv:hep-th/0307210)
-
Thomas Hartman, Leonardo Rastelli, Double-Trace Deformations, Mixed Boundary Conditions and Functional Determinants in AdS/CFT, JHEP 0801:019, 2008 (arXiv:hep-th/0602106)
Textbook account:
-
Sean Hartnoll, Andrew Lucas, Subir Sachdev, Section 1.7.3 of: Holographic quantum matter, MIT Press 2018 (arXiv:1612.07324, publisher)
(with an eye towards AdS/CFT in condensed matter physics)
Last revised on February 5, 2020 at 10:44:50. See the history of this page for a list of all contributions to it.