nLab little string

Idea

There is, by the brane scan, a superstring propagating in the 6-dimensional worldvolume of an NS5-brane. This is often called the little string of little string theory, with respect to the superstrings in the ambient 10-dimensional heterotic supergravity and type II supergravity that in turn the NS5-brane is propagating in.

Related concepts

• little string theory

The brane scan.

The Green-Schwarz type super $p$-brane sigma-models (see at table of branes for further links and see at The brane bouquet for the full classification):

$\stackrel{d}{=}$	$p =$	1	2	3	4	5	6	7	8	9
11			M2			M5
10	D0	F1, D1	D2	D3	D4	NS5, D5	D6	D7	D8	D9
9					*
8				*
7			M2${}_{top}$
6		F1${}_{little}$, S1${}_{sd}$		S3
5			*
4		*	*
3		*

(The first columns follow the exceptional spinors table.)

The corresponding exceptional super L-∞ algebra cocycles (schematically, without prefactors):

$\stackrel{d}{=}$	$p =$	1	2	3	4	5	6	7	8	9
11			$\Psi^2 E^2$ on sIso(10,1)			$\Psi^2 E^5 + \Psi^2 E^2 C_3$ on m2brane
10		$\Psi^2 E^1$ on sIso(9,1)	$B_2^2 + B_2 \Psi^2 + \Psi^2 E^2$ on StringIIA	$\cdots$ on StringIIB	$B_2^3 + B_2^2 \Psi^2 + B_2 \Psi^2 E^2 + \Psi^2 E^4$ on StringIIA	$\Psi^2 E^5$ on sIso(9,1)	$B_2^4 + \cdots + \Psi^2 E^6$ on StringIIA	$\cdots$ on StringIIB	$B_2^5 + \cdots + \Psi^2 E^8$ in StringIIA	$\cdots$ on StringIIB
9					$\Psi^2 E^4$ on sIso(8,1)
8				$\Psi^2 E^3$ on sIso(7,1)
7			$\Psi^2 E^2$ on sIso(6,1)
6		$\Psi^2 E^1$ on sIso(5,1)		$\Psi^2 E^3$ on sIso(5,1)
5			$\Psi^2 E^2$ on sIso(4,1)
4		$\Psi^2 E^1$ on sIso(3,1)	$\Psi^2 E^2$ on sIso(3,1)
3		$\Psi^2 E^1$ on sIso(2,1)

The Brane molecule

Furthermore, there exists a more general classification of possible supermembranes in spacetime with $S$ spatial dimensions and $T$ time dimensions, appearing in (Blencowe-Duff 88). In this sense, the brane scan is but the $T=1$ branch of the brane molecule. The objects appearing here are expected to be related to other generalizations of string theory. See D=12 supergravity and bosonic M-theory.

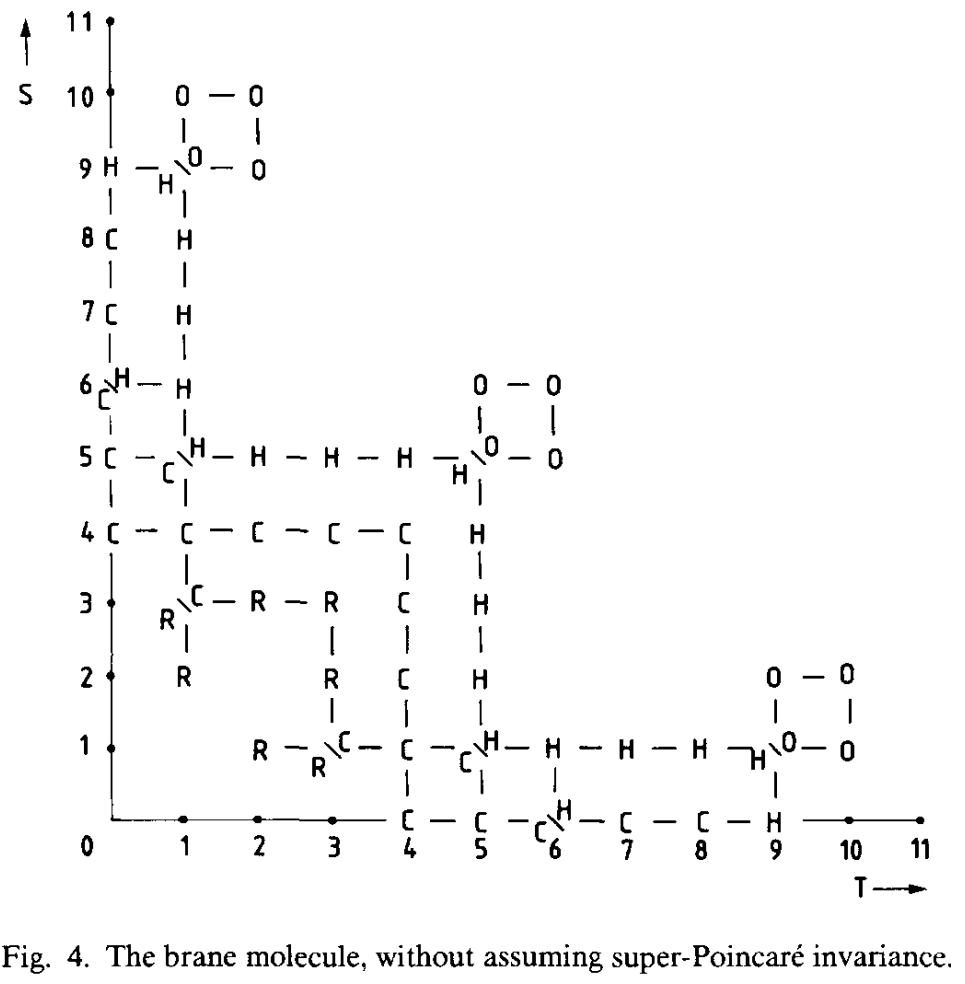
Compare:

• Miles Blencowe, Mike Duff, Supermembranes and the Signature of Space-time, Nucl. Phys. B310 (1988) 387-404 (spire:262142, 10.1016/0550-3213(88)90155-1, pdf)

• brane bouquet

References

See also

• Wikipedia, Little string theory

On D=3 N=4 super Yang-Mills theories with compact hyperkähler manifold Coulomb branches obtained by KK-compactification of little string theories:

• Kenneth Intriligator, Compactified Little String Theories and Compact Moduli Spaces of Vacua, Phys. Rev. D61:106005, 2000 (arXiv:hep-th/9909219)