nLab gluing function

Definition

Definition

(local chart and atlas and gluing function)

Given an $n$-dimensional topological manifold $X$ (def. ), then

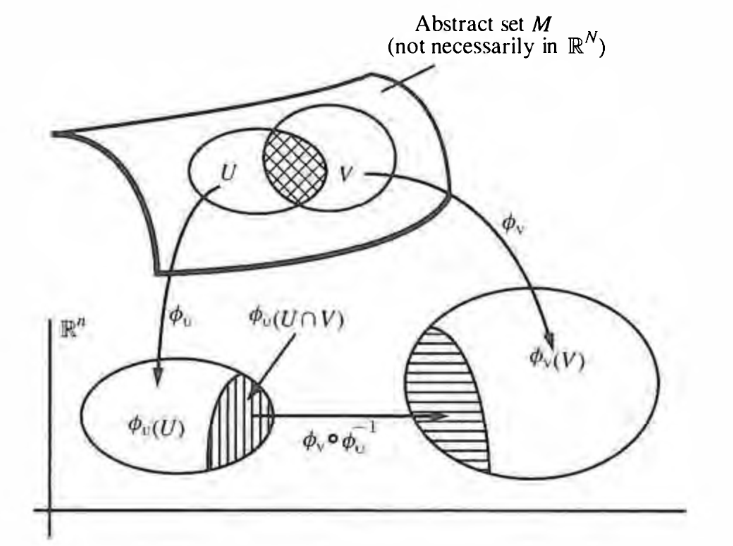
1. an open subset $U \subset X$ and a homeomorphism $\phi \colon \mathbb{R}^n \overset{\phantom{A}\simeq\phantom{A}}{\to} U$ is also called a local coordinate chart of $X$.

2. an open cover of $X$ by local charts $\left\{ \mathbb{R}^n \overset{\phi_i}{\to} U \subset X \right\}_{i \in I}$ is called an atlas of the topological manifold.

3. denoting for each $i,j \in I$ the intersection of the $i$th chart with the $j$th chart in such an atlas by

   $$U_{i j} \coloneqq U_i \cap U_j$$

   then the induced homeomorphism

   $$\mathbb{R}^n \supset \phantom{AA} \phi_i^{-1}(U_{i j}) \overset{\phantom{A}\phi_i\phantom{A}}{\longrightarrow} U_{i j} \overset{\phantom{A}\phi_j^{-1}\phantom{A}}{\longrightarrow} \phi_j^{-1}(U_{i j}) \phantom{AA} \subset \mathbb{R}^n$$

   is called the gluing function or coordinate transformation from chart $i$ to chart $j$.

graphics grabbed from Frankel

Related concepts

• transition function