nLab globe
Context
Higher category theory
Basic concepts
Basic theorems
- homotopy hypothesis-theorem
- delooping hypothesis-theorem
- periodic table
- stabilization hypothesis-theorem
- exactness hypothesis
- holographic principle
Applications
Models
- (n,r)-category
- Theta-space
- ∞-category/∞-category
- (∞,n)-category
- (∞,2)-category
- (∞,1)-category
- (∞,0)-category/∞-groupoid
- n-category = (n,n)-category
- n-poset = (n-1,n)-category
- n-groupoid = (n,0)-category
- categorification/decategorification
- geometric definition of higher category
- algebraic definition of higher category
- stable homotopy theory
Morphisms
Functors
Universal constructions
Extra properties and structure
1-categorical presentations
Contents
Idea
The cellular -globe is the globular analog of the cellular -simplex. It is one of the basic geometric shapes for higher structures.
Definition
The cellular -globe is the globular set represented by the object in the globe category :
Examples
The 0-globe is the singleton set, the category with a single morphism.
The 1-globe is the interval category.
The 3-globe looks like this
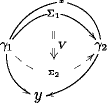
Properties
-Category structure
There is a unique structure of a strict omega-category, an n-category in fact, on the -globe. This makes the collection of -globes arrange themselves into a co-globular -category, i.e. a functor
Relation to simplices
The orientals translate between simplices and globes.
References
See the references at strict omega-category and at oriental.
Last revised on July 25, 2022 at 22:20:26. See the history of this page for a list of all contributions to it.