nLab cone (Riemannian geometry)
For other, related, concepts of a similar name see at cone.
Context
Riemannian geometry
Contents
Idea
In (pseudo-)Riemannian geometry, a cone is a part of a (pseudo-)Riemannian manifold where the metric tensor is locally of the form . The point that would correspond to is the “conical singularity”.
Examples
Spherical cones
The metric cone on the round sphere is simply Euclidean space
and hence may in fact be continued non-singularly also at the cone tip.
For a finite group with a free action on the round sphere , the quotient space exists as a Riemannian manifold. The metric cone on this is singular at the origin as soon as is not the trivial group.
If here is a cyclic group one says that this cone is obtained from flat Euclidean space by introducing a “deficit angle”.
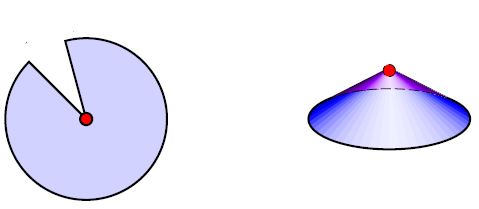
If one passes beyond smooth manifolds to orbifolds, then the cone tip in may be included. The result is the orbifold which is the homotopy quotient of Euclidean space by the linear -action (-representation).
Such conical singularities appear for instance in the far-horizon geometry of BPS black branes. Special cases are ADE-singularities.
-manifolds
-
Three examples of cones admitted by simply-connected G2-manifolds seem to be known: cones on , and . (Atiyah-Witten 01)
-
The metric cone over complex projective 3-space carries the structure of a G2-manifold whose Riemannian metric is invariant under the canonical Sp(2) action by left-matrix multiplication on homomogeneous coordinates in (Byant-Salamon 89, see also Acharya-Bryant-Salamon 20).
Related concepts
References
General
Discussion in the context of 3-manifolds and orbifolds:
- Daryl Cooper, Craig Hodgson, Steve Kerckhoff, Three-dimensional Orbifolds and Cone-Manifolds, MSJ Memoirs Volume 5, 2000 (pdf, euclid:1389985812)
Black brane conical singularities
Discussion of supergravity black brane-solutions at conical singularities (cone branes) includes the following (see also at far-horizon geometry)
-
Bobby Acharya, Jose Figueroa-O'Farrill, Chris Hull, B. Spence, Branes at conical singularities and holography, Adv. Theor.Math. Phys.2:1249-1286, 1999 (arXiv:hep-th/9808014)
-
Jose Figueroa-O'Farrill, Near-horizon geometries of supersymmetric branes, talk at SUSY 98 (arXiv:hep-th/9807149, talk slides)
-
Michael Atiyah, Edward Witten, -Theory dynamics on a manifold of -holonomy, Adv. Theor. Math. Phys. 6 (2001) (arXiv:hep-th/0107177)
A suggestion that there is an analogue of AdS-CFT duality for conical bulk spacetimes and their conical singularities:
- Rong-Xin Miao, Codimension- Holography for the Cones (arXiv:2101.10031)
-conifolds
On G2-conifolds (G2-manifolds with conical singularities):
Survey:
-
Spiro Karigiannis, -conifolds: A survey, 2014 (pdf)
-
Mark Haskins, Exotic Einstein metrics on and nearly Kähler 6-manifolds and -holonomy cones, 2016 (pdf)
Three simply connected -cones are known: the
-
metric cone on
-
metric cone on
-
Robert Bryant, Simon Salamon, On the construction of some complete metrics with exceptional holonomy, Duke Math. J. Volume 58, Number 3 (1989), 829-850 (euclid:euclid.dmj/1077307681)
-
Gary Gibbons, Don Page, Christopher Pope, Einstein metrics on , and bundles, Comm. Math. Phys. Volume 127, Number 3 (1990), 529-553 (euclid:cmp/1104180218)
More on the metric cone over complex projective 3-space as a G2-manifold:
- Bobby Acharya, Robert Bryant, Simon Salamon, A circle quotient of a cone, Differential Geometry and its Applications Volume 73, December 2020, 101681 (arXiv:1910.09518, doi:10.1016/j.difgeo.2020.101681)
Last revised on January 26, 2021 at 02:44:14. See the history of this page for a list of all contributions to it.