nLab comonoid

Definition

A comonoid (or comonoid object) in a monoidal category $\mathcal{M}$ is a monoid object $C$ in the opposite category $\mathcal{M}^{op}$ (which canonically becomes a monoidal category via the same tensor product operation as in $\mathcal{M}$).

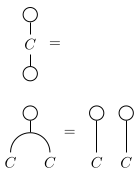
With the usual definition of monoids as having a unit, this means that a comonoid $C$ is equipped with a counit, which in string diagram-notation for $\mathcal{M}$ is of this form:

One speaks of a unital comonoid (or unital comonoid object; internal to Vect also called an augmented coalgebra) if $C$ is in addition equipped with a morphism $\eta \colon I \rightarrow C$

which verifies the properties that the unit would verify if $C$ was a bimonoid, ie. in string diagrams:

Examples

Example

(coassociative coalgebras) A comonoid object in VectorSpaces (with its usual tensor product of vector spaces) is called a coalgebra.

(Beware though that the term “coalgebra” is overused in many ways, for instance in coalgebras for endofunctor?. To be more specific to the linear-algebraic context one can say coassociative coalgebra.)

Example

(cartesian comonoids)
Every set carries a unique structure of a comonoid in the category of Sets with respect to the usual cartesian product.

Generally, every object $X \,\in\, \mathcal{C}$ in a cartesian monoidal category $(\mathcal{C}, \ast, \times)$ becomes (see also there) a (cocommutative) comonoid by taking the

• counit to be the terminal morphism $X \xrightarrow{\exists !} \ast$

• coproduct to be the diagonal morphism $diag_X \,\colon\, X \to X \times X$.

The analogous statement remains true for cartesian monoidal (infinity,1)-categories (see there).

Obvious as Exp. may be, it plays a somewhat profound role in various contexts:

Example

(suspension coring spectra)
In the case of topological spaces or other models of classical homotopy types, and using that the suspension spectrum-construction is a strong monoidal functor, Exp. implies the remarkable fact that suspension spectra carry coring spectrum-structure via smash-monoidal diagonals.

Related concepts

• coalgebra

• co-associativity

• co-unitality

(co)monad name	underlying endofunctor	(co)monad structure induced by
reader monad	$W \to (\text{-})$ on cartesian types	unique comonoid structure on $W$
coreader comonad	$W \times (\text{-})$ on cartesian types	unique comonoid structure on $W$
writer monad	$A \otimes (\text{-})$ on monoidal types	chosen monoid structure on $A$
cowriter comonad	$\array{A \to (\text{-}) \\ \\ A \otimes (\text{-})}$ on monoidal types	chosen monoid structure on $A$ chosen comonoid structure on $A$
Frobenius (co)writer	$\array{A \to (\text{-}) \\ A \otimes (\text{-})}$ on monoidal types	chosen Frobenius monoid structure