nLab cohomotopy charge map
Context
Manifolds and cobordisms
manifolds and cobordisms
cobordism theory, Introduction
Definitions
Genera and invariants
Classification
Theorems
Homotopy theory
homotopy theory, (∞,1)-category theory, homotopy type theory
flavors: stable, equivariant, rational, p-adic, proper, geometric, cohesive, directed…
models: topological, simplicial, localic, …
see also algebraic topology
Introductions
Definitions
Paths and cylinders
Homotopy groups
Basic facts
Theorems
Cohomology
Special and general types
-
group cohomology, nonabelian group cohomology, Lie group cohomology
-
-
cohomology with constant coefficients / with a local system of coefficients
Special notions
Variants
-
differential cohomology
Extra structure
Operations
Theorems
Contents
Idea
General
The Cohomotopy charge map is the function that assigns to a configuration of normally framed submanifolds of codimension their total charge as measured in -Cohomotopy-cohomology theory.
Concretely, this is the function which assigns to a normally framed submanifold its asymptotic normal distance function, namely the distance from the submanifold measured
-
in direction perpendicular to the submanifold, as encoded by the normal framing;
-
asymptotically, regarding all points outside a tubular neighbourhood as being at infinity.
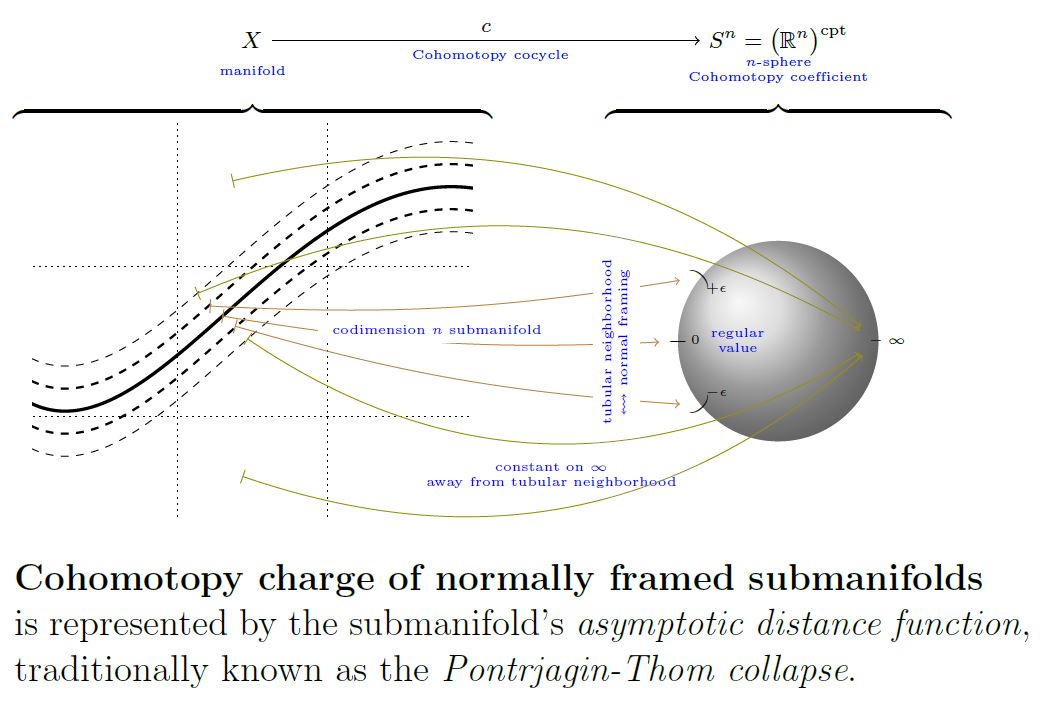
graphics grabbed from SS 19
For general this is known as the “Pontrjagin-Thom collapse construction”.
For charged points
For maximal codimension inside an oriented manifold, hence for 0-dimensional submanifolds, hence for configurations of points and with all points regarded as equipped with positive normal framing, the Cohomotopy charge map is alternatively known as the “electric field map” (Salvatore 01 following Segal 73, Section 1, see also Knudsen 18, p. 49) or the “scanning map” (Kallel 98, Manthorpe-Tillmann 13):
In maximal codimension , the Cohomotopy charge map is thus the continuous function
from the configuration space of points in the Euclidean space to the -Cohomotopy cocycle space vanishing at infinity on the Euclidean space(which is equivalently the space of pointed maps from the one-point compactification to itself, and hence equivalently the -fold iterated based loop space of the D-sphere), which sends a configuration of points in , each regarded as carrying unit charge to their total charge as measured in Cohomotopy-cohomology theory (Segal 73, Section 3).
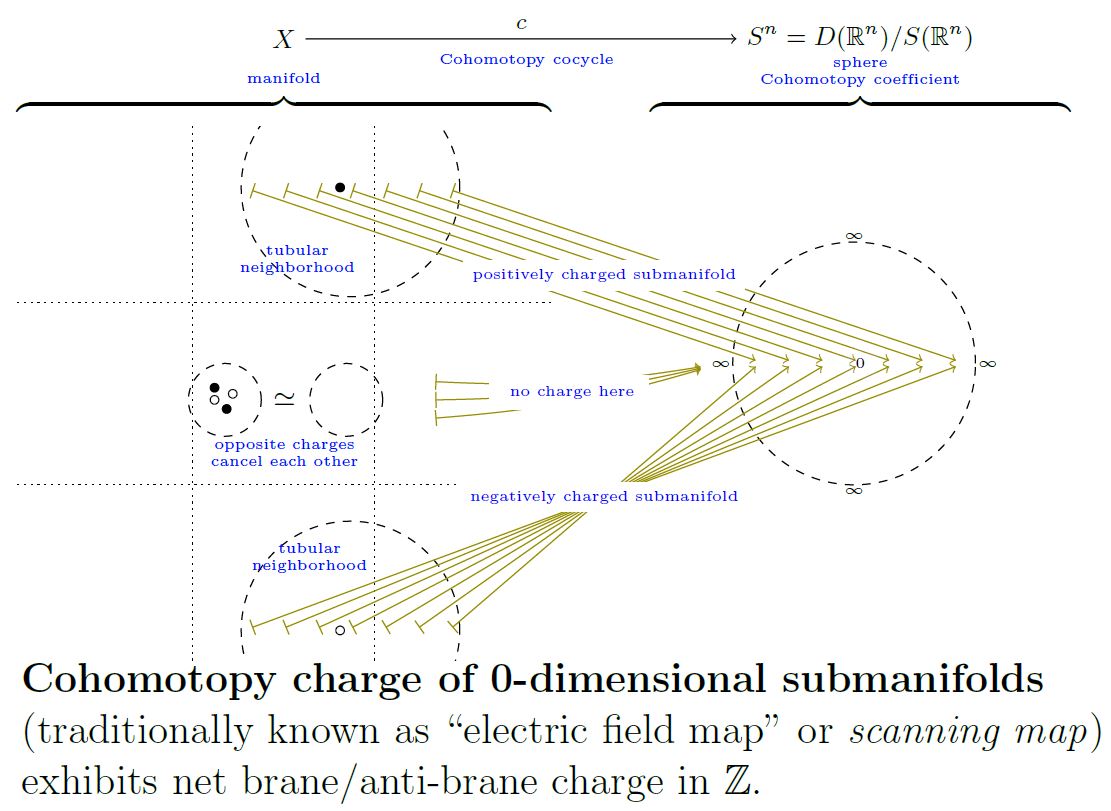
graphics grabbed from SS 19
(See also at cobordism – Relation to Cohomotopy.)
This has evident generalizations to other manifolds than just Euclidean spaces, to spaces of labeled configurations and to equivariant Cohomotopy. The following graphics illustrates the Cohomotopy charge map on G-space tori for with values in -equivariant Cohomotopy:
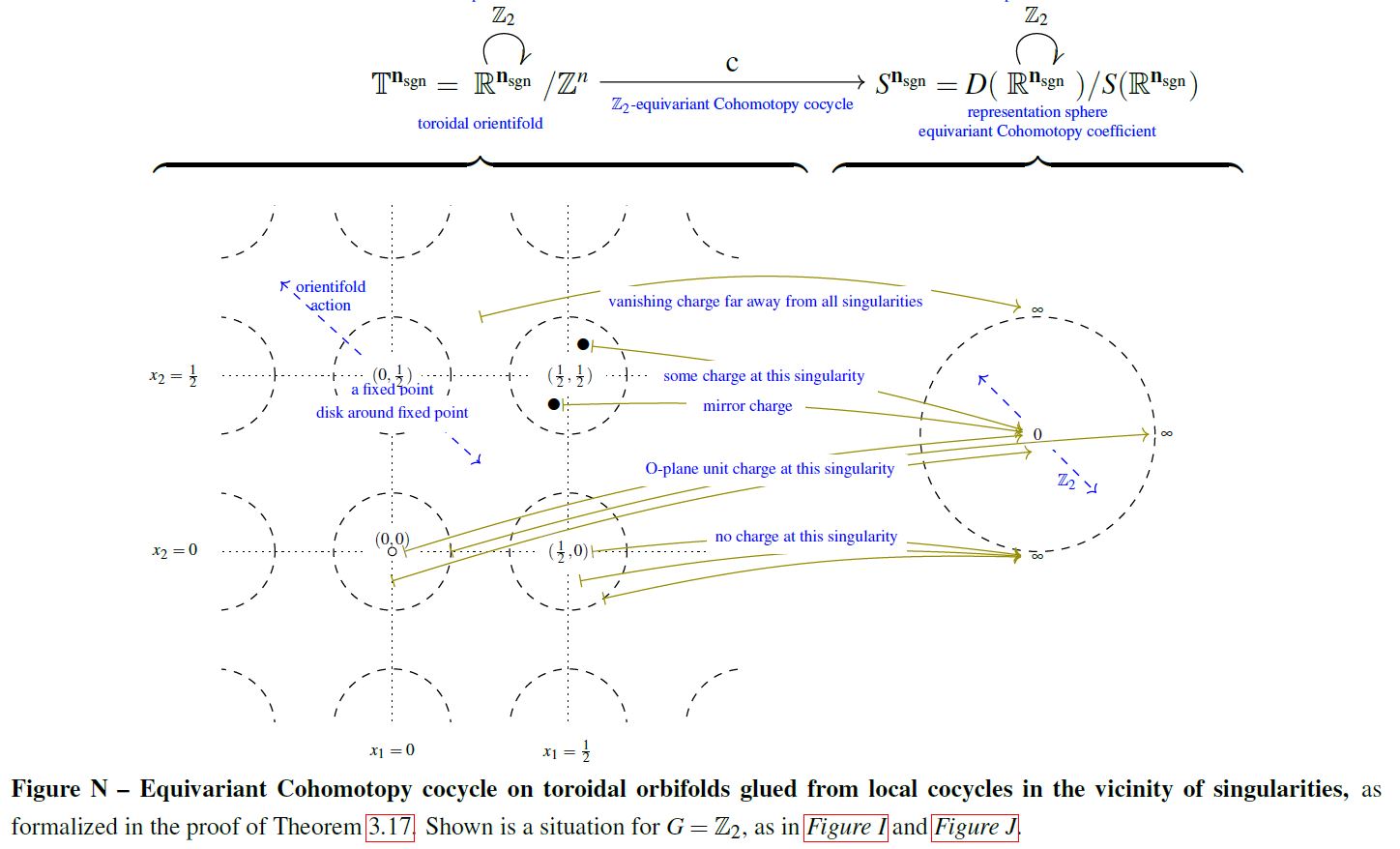
graphics grabbed from SS 19
Properties
Characterization of cobordism classes by their Cohomotopy charge
The unstable Pontrjagin-Thom theorem states that Cohomotopy charge faithfully reflects configurations of normally framed submanifolds up to normally framed embedded cobordism, hence that the Pontrjagin-Thom collapse construction induces a bijection between cobordism classes of normally framed submanifolds and the Cohomotopy set in degree the respective codimension:
For more details see here.
In good situations this bijection of sets of homotopy classes enhances to a weak equivalence of configuration spaces/cocycle spaces. See Characterization of point configurations by their Cohomotopy charge below.
Characterization of point configurations by their Cohomotopy charge
In some situations the Cohomotopy charge map is a weak homotopy equivalence and hence exhibits, for all purposes of homotopy theory, the Cohomotopy cocycle space of Cohomotopy charges as an equivalent reflection of the configuration space of points.
On Euclidean spaces via plain Cohomotopy
Proposition
(group completion on configuration space of points is iterated based loop space)
from the full unordered and unlabeled configuration space (here) of Euclidean space to the -fold iterated based loop space of the D-sphere, exhibits the group completion (here) of the configuration space monoid
Proposition
(Cohomotopy charge map is weak homotopy equivalence on sphere-labeled configuration space of points)
For with , the Cohomotopy charge map (1)
is a weak homotopy equivalence from the configuration space (here) of unordered points with labels in and vanishing at the base point of the label space to the -fold iterated loop space of the D+k-sphere.
On closed manifolds via twisted Cohomotopy
The May-Segal theorem generalizes from Euclidean space to closed smooth manifolds if at the same time one passes from plain Cohomotopy to twisted Cohomotopy, twisted, via the J-homomorphism, by the tangent bundle:
Proposition
Let
-
be a smooth closed manifold of dimension ;
Then the Cohomotopy charge map constitutes a weak homotopy equivalence
between
-
the J-twisted (n+k)-Cohomotopy space of , hence the space of sections of the -spherical fibration over which is associated via the tangent bundle by the O(n)-action on
-
the configuration space of points on with labels in .
(Bödigheimer 87, Prop. 2, following McDuff 75)
Remark
In the special case that the closed manifold in Prop. is parallelizable, hence that its tangent bundle is trivializable, the statement of Prop. reduces to this:
Let
-
be a parallelizable closed manifold of dimension ;
Then the Cohomotopy charge map constitutes a weak homotopy equivalence
between
-
-Cohomotopy space of , hence the space of maps from to the (n+k)-sphere
-
the configuration space of points on with labels in .
References
Pontrjagin-Thom construction
Pontrjagin’s construction
General
The Pontryagin theorem, i.e. the unstable and framed version of the Pontrjagin-Thom construction, identifying cobordism classes of normally framed submanifolds with their Cohomotopy charge in unstable Borsuk-Spanier Cohomotopy sets, is due to:
-
Lev Pontrjagin, Classification of continuous maps of a complex into a sphere, Communication I, Doklady Akademii Nauk SSSR 19(3) (1938), 147-149
-
Lev Pontryagin, Homotopy classification of mappings of an (n+2)-dimensional sphere on an n-dimensional one, Doklady Akad. Nauk SSSR (N.S.) 19 (1950), 957–959 (pdf)
(both available in English translation in Gamkrelidze 86),
as presented more comprehensively in:
- Lev Pontrjagin, Smooth manifolds and their applications in Homotopy theory, Trudy Mat. Inst. im Steklov, No 45, Izdat. Akad. Nauk. USSR, Moscow, 1955 (AMS Translation Series 2, Vol. 11, 1959) (doi:10.1142/9789812772107_0001, pdf)
The Pontrjagin theorem must have been known to Pontrjagin at least by 1936, when he announced the computation of the second stem of homotopy groups of spheres:
- Lev Pontrjagin, Sur les transformations des sphères en sphères (pdf) in: Comptes Rendus du Congrès International des Mathématiques – Oslo 1936 (pdf)
Review:
-
Daniel Freed, Karen Uhlenbeck, Appendix B of: Instantons and Four-Manifolds, Mathematical Sciences Research Institute Publications, Springer 1991 (doi:10.1007/978-1-4613-9703-8)
-
Antoni Kosinski, chapter IX of: Differential manifolds, Academic Press (1993) [pdf, ISBN:978-0-12-421850-5]
-
John Milnor, Chapter 7 of: Topology from the differentiable viewpoint, Princeton University Press, 1997. (ISBN:9780691048338, pdf)
-
Mladen Bestvina (notes by Adam Keenan), Chapter 16 in: Differentiable Topology and Geometry, 2002 (pdf)
-
Michel Kervaire, La méthode de Pontryagin pour la classification des applications sur une sphère, in: E. Vesentini (ed.), Topologia Differenziale, CIME Summer Schools, vol. 26, Springer 2011 (doi:10.1007/978-3-642-10988-1_3)
-
Rustam Sadykov, Section 1 of: Elements of Surgery Theory, 2013 (pdf, pdf)
-
András Csépai, Stable Pontryagin-Thom construction for proper maps, Period Math Hung 80, 259–268 (2020) (arXiv:1905.07734, doi:10.1007/s10998-020-00327-0)
Discussion of the early history:
Twisted/equivariant generalizations
The (fairly straightforward) generalization of the Pontrjagin theorem to the twisted Pontrjagin theorem, identifying twisted Cohomotopy with cobordism classes of normally twisted-framed submanifolds, is made explicit in:
- James Cruickshank, Lemma 5.2 using Sec. 5.1 in: Twisted homotopy theory and the geometric equivariant 1-stem, Topology and its Applications Volume 129, Issue 3, 1 April 2003, Pages 251-271 (doi:10.1016/S0166-8641(02)00183-9)
A general equivariant Pontrjagin theorem – relating equivariant Cohomotopy to normal equivariant framed submanifolds – remains elusive, but on free G-manifolds it is again straightforward (and reduces to the twisted Pontrjagin theorem on the quotient space), made explicit in:
- James Cruickshank, Thm. 5.0.6, Cor. 6.0.13 in: Twisted Cobordism and its Relationship to Equivariant Homotopy Theory, 1999 (pdf, pdf)
In negative codimension
In negative codimension, the Cohomotopy charge map from the Pontrjagin theorem gives the May-Segal theorem, now identifying Cohomotopy cocycle spaces with configuration spaces of points:
-
Peter May, The geometry of iterated loop spaces, Springer 1972 (pdf)
-
Graeme Segal, Configuration-spaces and iterated loop-spaces, Invent. Math. 21 (1973), 213–221. MR 0331377 (pdf)
c Generalization of these constructions and results is due to
-
Dusa McDuff, Configuration spaces of positive and negative particles, Topology Volume 14, Issue 1, March 1975, Pages 91-107 (doi:10.1016/0040-9383(75)90038-5)
-
Carl-Friedrich Bödigheimer, Stable splittings of mapping spaces, Algebraic topology. Springer 1987. 174-187 (pdf, pdf)
Thom’s construction
Thom's theorem i.e. the unstable and oriented version of the Pontrjagin-Thom construction, identifying cobordism classes of normally oriented submanifolds with homotopy classes of maps to the universal special orthogonal Thom space , is due to:
- René Thom, Quelques propriétés globales des variétés différentiables, Comment. Math. Helv. 28, (1954). 17-86 (doi:10.1007/BF02566923, dml:139072, digiz:GDZPPN002056259, pdf)
Textbook accounts:
- Robert Stong, Notes on Cobordism theory, 1968 (toc pdf, publisher page)
Lashof’s construction
The joint generalization of Pontryagin 38a, 55 (framing structure) and Thom 54 (orientation structure) to any family of tangential structures (“(B,f)-structure”) is first made explicit in
- Richard Lashof, Poincaré duality and cobordism, Trans. AMS 109 (1963), 257-277 (doi:10.1090/S0002-9947-1963-0156357-4)
and the general statement that has come to be known as the Pontryagin-Thom isomorphism (identifying the stable cobordism classes of normally (B,f)-structured submanifolds with homotopy classes of maps to the Thom spectrum Mf) is really due to Lashof 63, Theorem C.
Textbook accounts:
-
Theodor Bröcker, Tammo tom Dieck, Satz 3.1 & 4.9 in: Kobordismentheorie, Lecture Notes in Mathematics 178, Springer (1970) [ISBN:9783540053415]
-
Stanley Kochman, section 1.5 of: Bordism, Stable Homotopy and Adams Spectral Sequences, AMS 1996
-
Yuli Rudyak, On Thom spectra, Orientability and Cobordism, Springer 1998 (pdf)
Lecture notes:
-
John Francis, Topology of manifolds course notes (2010) (web), Lecture 3: Thom’s theorem (pdf), Lecture 4 Transversality (notes by I. Bobkova) (pdf)
-
Cary Malkiewich, Section 3 of: Unoriented cobordism and , 2011 (pdf)
-
Tom Weston, Part I of An introduction to cobordism theory (pdf)
See also:
For point configurations
The theorem that, with due care, for point configurations the Cohomotopy charge map is in fact a weak homotopy equivalence between the configuration space of points and the Cohomotopy cocycle space originates with
-
Peter May, The geometry of iterated loop spaces, Springer 1972 (pdf)
-
Graeme Segal, Configuration-spaces and iterated loop-spaces, Invent. Math. 21 (1973), 213–221. MR 0331377 (pdf)
-
Dusa McDuff, Configuration spaces of positive and negative particles, Topology Volume 14, Issue 1, March 1975, Pages 91-107 (doi:10.1016/0040-9383(75)90038-5)
with comprehensive review in
- Carl-Friedrich Bödigheimer, Stable splittings of mapping spaces, Algebraic topology. Springer 1987. 174-187 (pdf, pdf)
See also:
-
Sadok Kallel, Spaces of particles on manifolds and Generalized Poincaré Dualities, The Quarterly Journal of Mathematics, Volume 52, Issue 1, 1 March 2001 (doi:10.1093/qjmath/52.1.45)
-
Paolo Salvatore, Configuration spaces with summable labels, In: Aguadé J., Broto C., Carles Casacuberta (eds.) Cohomological Methods in Homotopy Theory. Progress in Mathematics, vol 196. Birkhäuser, Basel, 2001 (arXiv:math/9907073)
-
Oscar Randal-Williams, section 10 of: Embedded Cobordism Categories and Spaces of Manifolds, Int. Math. Res. Not. IMRN 2011, no. 3, 572-608 (arXiv:0912.2505)
-
Richard Manthorpe, Ulrike Tillmann, Tubular configurations: equivariant scanning and splitting, Journal of the London Mathematical Society, Volume 90, Issue 3 (arxiv:1307.5669, doi:10.1112/jlms/jdu050)
-
Ben Knudsen, Configuration spaces in algebraic topology (arXiv:1803.11165)
-
Hisham Sati, Urs Schreiber, Equivariant Cohomotopy implies orientifold tadpole cancellation (arXiv:1909.12277)
Last revised on May 9, 2022 at 13:08:46. See the history of this page for a list of all contributions to it.