nLab braid group statistics
Context
Topological physics
Topological Physics – Phenomena in physics controlled by the topology (often: the homotopy theory) of the physical system.
General theory:
In metamaterials:
-
topological phononics (sound waves?)
For quantum computation:
Contents
- Anyon braiding
- As generalized boson/fermion statistics?
- Braiding of anyonic quanta – via “fictitious” AB-phases
- Braiding of anyonic defects – via adiabatic Berry phases
- Related concepts
- References
- General
- Anyonic topological order in terms of braided fusion categories
- Anyons in the quantum Hall liquids
- Anyons in topological superconductors
- Experimental detection of anyons
- Defect anyons
- Anyons in momentum-space
- Topological quantum computation with anyons
- Braid group representations (as topological quantum gates)
- Compilation to braid gate circuits
Anyon braiding
In quantum physics, braid group statistics or anyon statistics (sometimes: plektons) refers to an exotic phenomenon where the braiding of the worldlines of certain effective particles (“anyons”) in an effectively 2+1-dimensional spacetime has the effect of transforming the quantum state of the total quantum system by unitary operators which constitute a linear representation of the braid group – a braid representation.
Often this is motivated as a generalization of the boson- or fermion-“statistics” which enters the spin-statistics theorem, see below.
But the actual mathematical nature of anyons must be different from that of elements of boson/fermion-Fock spaces and often remains somewhat vague in existing discussions. One may recognize two different more concrete conceptualizations of anyons in the literature:
-
anyonic quanta much like boson/fermion quanta but subject to an additional global interaction by Aharonov-Bohm phases due to a flat fictitious gauge field which is sourced by and coupled to each of the quanta;
(this goes back to Arovas, Schrieffer, Wilczek & Zee 1985, further developed in Chen, Wilczek, Witten & Halperin 1989, see below)
-
anyonic defects like vortices or other solitons, whose position is a classical parameter to the quantum system, the adiabatic movement of which acts by Berry phases on the quantum ground state.
(e.g. Avros, Schrieffer & Wilczek 1984, see further below)
The concept of anyons is particularly well motivated in solid state physics, where effectively 2-dimensional quantum materials are common place (eg. graphene) or where particles may otherwise be constrained to move in a plane, such as in the quantum Hall effect. There is a multitude of models in condensed matter theory (mostly lattice models, such as string-net models) which theoretically realize anyon braid group statistics, and there are some first experimental indications of anyonic phenomena in actual materials (see the references under Experimental Realization) below.
Specifically, in the context of topological phases of matter, the (potential) presence of anyons has come to be known as the case of topological order, see there for more.
Besides general curiosity, much of the interest in anyonic braid group statistics lies in the fact that these braid representations are imagined to potentially serve as quantum gates in topological quantum computers. See there for more.
As generalized boson/fermion statistics?
In quantum field theory, one speaks of the “statistics” of a particle species when referring to the linear representation that -particle wavefunctions form under the the symmetric group which permutes the particles.
While there is a rich representation theory of the symmetric group, the spin-statistics theorem says, when it applies, that for field quanta only the simplest two possibilities may occur:
-
bosons (such as photons) transform under the trivial representation of ,
-
fermions (such as electrons) transform under the sign representation of .
(see also at Slater determinant)
Now, the braid group on strands covers the symmetric group
which allows one to regard any linear representation of the symmetric group also as a particular braid group representation. But by its definition, the braid group may be understood as the group of isotopy-classes of disjoint timelike worldlines in an effectively 2+1 dimensional spacetime, with the group operation being concatenation of worldlines.
In this sense, one may imagine that any braid group representations may generalize the boson/fermion statistics in 2+1 dimensions. Texts typically suggest that this applies to quasiparticles.
The term anyon (due to Wilczek 1982b) is a pun on this state of affairs that any statistics “in between” boson- and fermion-statistics may be allowed.
On the other hand, anyonic braiding is conceptually different from boson/fermion statistics – if it were on the same footing then the spin-statistics theorem would rule out anyonic braiding. This is acknowledged by Chen, Wilczek, Witten & Halperin 1989, p. 352 (cf. also Wilczek 1990, §I.2, pp. 11):
Once the permutation group is replaced by the braid group, the simple construction of passing from the solution to the one-particle problems to the solution of many-particle problems, familiar from the free bosons and free fermions, does not work anymore.
Braiding of anyonic quanta – via “fictitious” AB-phases
A concrete model for anyonic quanta via otherwise free fermions in 2d interacting through a flat “fictitious gauge field” was proposed in Arovas, Schrieffer, Wilczek & Zee 1985 and developed in Chen, Wilczek, Witten & Halperin 1989 and Iengo & Lechner 1992 (the model has been advertized in early reviews, e.g. Wilczek 1990, §I.3 and Wilczek 1991, but seems not to have been developed much since):
This model regards anyons as a priori free fermions, but equipped now with a non-local mutual interaction via a “fictitious gauge field” (CWWH89, §2), in that each of the particles is modeled as the singular source of a flat circle connection (a vector potential with vanishing field strength), which hence exerts no Lorentz force but has the effect that globally each other particle is subject to the same Aharonov-Bohm effect as would be caused by a tuple of infinite solenoids piercing through each of the other particle’s positions.
For emphasis, from CWWH89, p. 359:
Here the particles are to be regarded (in the absence of interactions) as fermions; the interaction then makes them anyons with statistical parameter .
It follows (Wu 1984, Imbo, Imbo & Sudarshan 1990) that (quoting from Fröhlich, Gabbiani & Marchetti 1990, p. 20):
If the Hilbert space of anyon wave functions must be chosen to be a space of multi-valued functions with half-monodromies given by the phase factors . Such wave functions can be viewed as single-valued functions on the universal cover of the configuration space of points.
Further discussion of anyon-wavefunctions as multi-valued functions on a configuration space of points, hence equivariant functions on its universal cover: BCMS93, §1, Mund & Schrader 1995, DFT97, §1 Myrheim 1999, DMV03, Murthy & Shankar 2009
Incidentally, the quasi-particle-excitations of (or in) a gas of such Aharonov-Bohm phased anyons are argued to be vortices (CWWH89, p. 457):
we are led to conclude that in anyon superconductivity, charged quasi-particles and vortices do not constitute two separate sorts of elementary excitations - they are one and the same.
This seamlessly leads over to:
Braiding of anyonic defects – via adiabatic Berry phases
In practice, many (most?) incarnations of the concept of anyons are anyonic defects – non-perturbative solitonic defects (of codimension=2), akin to vortices in fluids:
Anyonic particles are best viewed as a kind of topological defects that reveal non-trivial properties of the ground state. Kitaev 2006, p. 4
Anyons can arise in two ways: as localised excitations of an interacting quantum Hamiltonian or as defects in an ordered system. Das Sarma, Freedman & Nayak 2015, p. 1
(Compare also the original discussions in Goldin, Menikoff & Sharp 1981, §III, Wilczek 1982a & Wilczek 1990, p. 5, which offer a quantum particle “bound” to a classical & infinite solenoid – hence a 2d magnetic monopole defect – as a decent model for an anyon.)
But defects are a kind of boundary conditions, hence external parameters or background fields for the actual quantum field.
Concretely, a widely appreciated proposal (Moore & Read 1991, Read & Rezayi 1999) identifies anyonic ground state wavefunctions with conformal blocks of a 2d CFT – hence with Chern-Simons theory states – with prescribed poles at the location of the anyons.
Now the quantum adiabatic theorem says that the sufficiently slow motion of such external parameters transforms the quantum ground state by unitary operators (“Berry phases”, see also at adiabatic quantum computation). This suggests (Avros, Schrieffer & Wilczek 1984, p. 1, Freedman, Kitaev, Larsen & Wang 2003, pp. 6, Nayak, Simon, Stern & Freedman 2008, §II.A.2 (p. 6), Cheng, Galitski & Das Sarma 2011, p. 1) that:
Definition
(adiabatic defect braiding)
Anyon braiding statistics is the braid group representation on a quantum ground state induced by adiabatic braiding of topological codimension=2 defects in their configuration space.
Here
-
for point-defects the “configuration space” is the configuration space of points in a surface (as briefly touched upon already in Leinaas & Myrheim 1977, pp. 22, Wilczek 1982b, p. 959), such as in the plane, in which case its fundamental group is the braid group;
-
“topological” is meant as in topological quantum field theory: The induced adiabatic unitary transformation is demanded/assumed to depend only on the isotopy-class of the defect-worldlines, hence only on the underlying braid-pattern.
This notion of anyon “statistics” is at least tacitly implicit in much of the literature on anyons in topological quantum computation, such as in the popular graphics depicting anyon worldlines as the Wilson lines in Chern-Simons theory. (see the graphics below).
Indeed, the effects of adiabatic braiding of defects in quantum materials has been understood and discussed before and in parallel to the term “anyon” becoming established: Mermin 1979, Lo & Preskill 1993.
A concrete realistic example of defect anyons are vortex anyons see below. But the notion of codimension=2 defects subsumes situations that are quite different from the quasiparticle-excitations imagined in traditional texts on anyons, such as:
Vortex anyons
Specifically, vortex anyons are realized in Bose-Einstein condensates (MPSS19, following PFCZ01) and in (other) superfluids (MMN21).
In fact, defect-type vortex anyons generically appear in condensates of non-defect anyons (CDLR19):
A theoretical model of vortex anyons in a Higgs field coupled to Chern-Simons theory is discussed in Fröhlich & Marchetti 1988. An instructive lattice model of vortex anyons is analyzed in detail in Kitaev 2006.
Much attention in current efforts towards realizing topological quantum computation is being paid to anyons realized as Majorana zero modes bound to vortices (Das Sarma, Freedman & Nayak 2015, cf. MMBDRSC19).
This situation may generalize to parafermion-su(2)-anyons, where
each (anti)soliton carries parafermion zero mode which supplies it with the non-Abelian statistics Tsvelik 2014a, p. 2, cf. Borcherding 2018, pp. 3.
Braiding of nodal points in momentum space (graphics from MMBDRSC19, Fig. 1):
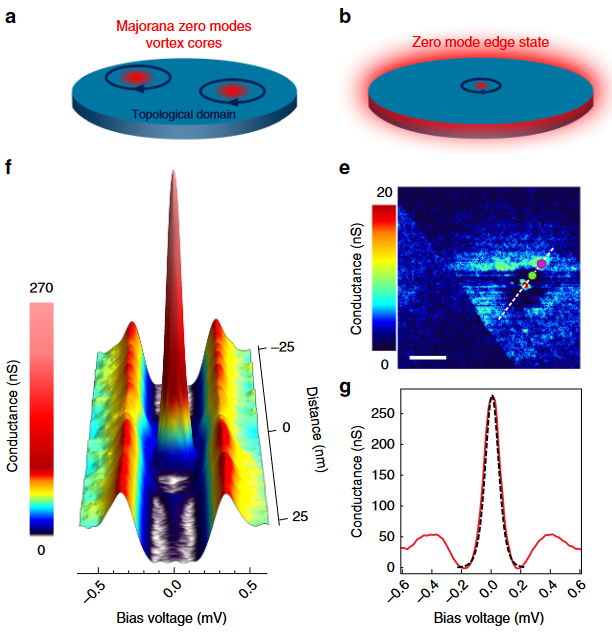
Anyonic band nodes?
Around 2020 the view has been emerging that also defects “in momentum/reciprocal space” may behave as anyonic defects under braiding in momentum space. This applies concretely to nodal points (where electron bands touch or cross) in the momentum space Brillouin torus of topological semi-metals:
here are band crossing points, henceforth called vortices Ahnm Park & Yang 2019
a new type non-Abelian “braiding” of nodal-line rings inside the momentum space Tiwari & Bzdušek 2020
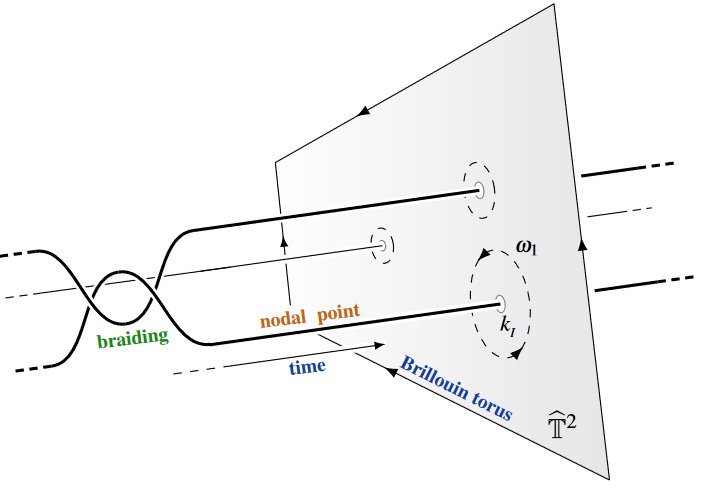
(graphics from SS22)
Curiously, these reciprocal/momemtum space anyons lend themselves to tractable laboratory manipulation in a way that has remained notoriously elusive for “position space” anyons:
Our work opens up routes to readily manipulate Weyl nodes using only slight external parameter changes, paving the way for the practical realization of reciprocal space braiding CBSM22,
specifically
it is possible to controllably braid Kagome band nodes in monolayer using strain and/or an external electric field PBMS22,
leading to:
new opportunities for exploring non-Abelian braiding of band crossing points (nodes) in reciprocal space, providing an alternative to the real space braiding exploited by other strategies.
Real space braiding is practically constrained to boundary states, which has made experimental observation and manipulation difficult; instead, reciprocal space braiding occurs in the bulk states of the band structures and we demonstrate in this work that this provides a straightforward platform for non-Abelian braiding. PBSM22.
Defect branes
In string theory, defect branes are D-branes or M-branes of codimension=2, such as D7-branes in type IIB string theory or M5-brane-intersections on “M3-branes” in M-theory.
It has been suggest in deBoer & Shigemori 2012, p. 65 that these could behave like anyons. This is further substantiated in SS22. See there for more.
Related concepts
References
General
The concept of anyons satisfying braid group statistics originated independently in:
-
Jon Magne Leinaas, Jan Myrheim, On the theory of identical particles, К теории тождествениых частиц, Nuovo Cim B 37, 1–23 (1977) (doi:10.1007/BF02727953)
-
G. A. Goldin, R. Menikoff, D. H. Sharp, Representations of a local current algebra in nonsimply connected space and the Aharonov–Bohm effect, J. Math. Phys. 22 1664 (1981) doi:10.1063/1.525110
-
Frank Wilczek, Magnetic Flux, Angular Momentum, and Statistics, Phys. Rev. Lett. 48 (1982) 1144 (reprinted in Wilczek 1990, p. 163-165) doi:10.1103/PhysRevLett.48.1144
The term anyon was introduced in:
- Frank Wilczek, Quantum Mechanics of Fractional-Spin Particles, Phys. Rev. Lett. 49 (1982) 957 (reprinted in Wilczek 1990, p. 166-168) doi:10.1103/PhysRevLett.49.957
Identification of anyon phases (specifically in the quantum Hall effect) as Berry phases of an adiabatic transport of anyon positions:
- Daniel P. Arovas, John Robert Schrieffer, Frank Wilczek, Fractional Statistics and the Quantum Hall Effect, Phys. Rev. Lett. 53, 722 (1984) doi:10.1103/PhysRevLett.53.722
The “fictitious gauge field”-method for modelling anyons:
-
Daniel P. Arovas, Robert Schrieffer, Frank Wilczek, Anthony Zee, Statistical mechanics of anyons, Nuclear Physics B 251 (1985) 117-126 (reprinted in Wilczek 1990, p. 173-182) doi:10.1016/0550-3213(85)90252-4
-
Yi-Hong Chen, Frank Wilczek, Edward Witten, Bertrand Halperin, On Anyon Superconductivity, International Journal of Modern Physics B 03 07 (1989) 1001-1067 (reprinted in Wilczek 1990, p. 342-408) doi:10.1142/S0217979289000725, pdf
-
Frank Wilczek, States of Anyon Matter, International Journal of Modern Physics B 05 09 (1991) 1273-1312 [doi:10.1142/S0217979291000626]
and with specific emphasis on the resulting (abelian!) Chern-Simons theory:
- Roberto Iengo, Kurt Lechner, Anyon quantum mechanics and Chern-Simons theory, Physics Reports 213 4 (1992) 179-269 [doi:10.1016/0370-1573(92)90039-3]
The suggestion that the anyonic ground state-wavefunctions are essentially conformal blocks of 2d CFT (notably for su(2)-anyons):
-
Gregory Moore, Nicholas Read, Nonabelions in the fractional quantum hall effect, Nuclear Physics B 360 2–3 (1991) 362-396 doi:10.1016/0550-3213(91)90407-O, pdf
-
Nicholas Read, Edward Rezayi, Beyond paired quantum Hall states: Parafermions and incompressible states in the first excited Landau level, Phys. Rev. B 59 (1999) 8084 doi:10.1103/PhysRevB.59.8084
More comprehensive accounts of anyons:
-
Frank Wilczek, Fractional Statistics and Anyon Superconductivity, World Scientific (1990) [doi:10.1142/0961]
-
Alexei Kitaev, Anyons in an exactly solved model and beyond, Annals of Physics 321 1 (2006) 2-111 [doi:10.1016/j.aop.2005.10.005]
-
Eduardo Fradkin, Anyon superconductivity, Chapter 11 in: Field Theories of Condensed Matter Physics, Cambridge University Press (2013) 414-431 [ISBN: 9781139015509, doi:10.1017/CBO9781139015509.013]
See also:
- Martin Greiter, Frank Wilczek, Fractional Statistics [arXiv:2210.02530]
Rigorous discussion in terms of superselection sectors in algebraic quantum field theory:
-
Jürg Fröhlich, Pieralberto Marchetti, Quantum field theory of anyons, Lett. Math. Phys. 16 (1988) 347–358 (reprinted in Wilczek 1990, p. 202-213) doi:10.1007/BF00402043
-
Jürg Fröhlich, Fabrizio Gabbiani, Braid statistics in local quantum theory, Reviews in Mathematical Physics, 2 03 (1990) 251-353 doi:10.1142/S0129055X90000107
-
Jürg Fröhlich, Fabrizio Gabbiani, Pieralberto Marchetti, Braid statistics in three-dimensional local quantum field theory, in: H.C. Lee (ed.) Physics, Geometry and Topology NATO ASI Series, 238 Springer (1990) doi:10.1007/978-1-4615-3802-8_2, pdf
-
Klaus Fredenhagen, Karl-Henning Rehren, Bert Schroer, Superselection sectors with braid group statistics and exchange algebras – I: General theory, Comm. Math. Phys. Volume 125, Number 2 (1989), 201-226. (euclid:cmp/1104179464)
-
Klaus Fredenhagen, Karl-Henning Rehren, Bert Schroer, Superselection sectors with braid group statistics and exchange algebras – II: Geometric aspects and conformal covariance, Reviews in Mathematical PhysicsVol. 04, No. spec01, pp. 113-157 (1992) (doi:10.1142/S0129055X92000170 pdf)
Discussion of anyon-wavefunctions as multi-valued functions on a configuration space of points:
-
Yong-Shi Wu, Multiparticle Quantum Mechanics Obeying Fractional Statistics, Phys. Rev. Lett. 53 (1984) 111 doi:10.1103/PhysRevLett.53.111, pdf
-
Tom Imbo, Chandni Shah Imbo, E. C. G. Sudarshan, Identical particles, exotic statistics and braid groups, Physics Letters B 234 1–2, (1990) 103-107 doi:10.1016/0370-2693(90)92010-G, pdf
-
Garth A. Baker, Geoff S. Canright, Shashikant B. Mulay, Carl Sundberg, On the spectral problem for anyons, Communications in Mathematical Physics 153 (1993) 277–295 doi:10.1007/BF02096644
-
J. Mund, Robert Schrader, Hilbert Spaces for Nonrelativistic and Relativistic “Free” Plektons (Particles with Braid Group Statistics), in Advances in dynamical systems and quantum physics (Capri, 1993), World Sci. (1995) 235–259 arXiv:hep-th/9310054
followed up by:
Klaus Fredenhagen, Matthias Gaberdiel and Stefan M. Rüger, Scattering states of plektons (particles with braid group statistics) in 2+1 dimensional quantum field theory, Communications in Mathematical Physics 175 (1996) 319–335 doi:10.1007/BF02102411
-
Gianfausto Dell’Antonio, Rodolfo Figari & Alessandro Teta, Statistics in Space Dimension Two, Letters in Mathematical Physics 40 (1997) 235–256 doi:10.1023/A:1007361832622
-
Jan Myrheim, Anyons, p. 265-414 in: Topological aspects of low dimensional systems, Les Houches LXIX, Springer (1999) doi:10.1007/3-540-46637-1, pdf
-
M.V.N. Murthy, Ramamurti Shankar, Exclusion Statistics: From Pauli to Haldane (1999, 2009) dspace:123456789/334, pdf, pdf
-
G. Date, M.V.N. Murthy, Radhika Vathsan, Classical and Quantum Mechanics of Anyons arXiv:cond-mat/0302019
The topic of quantum measurement of non-abelian anyons is crucial to their identification in experiment but has received little attenion, exceptions being:
-
Parsa Bonderson, Kirill Shtengel, Joost Slingerland, Decoherence of Anyonic Charge in Interferometry Measurements, Phys. Rev. Lett. 98 (2007) 070401 [doi:10.1103/PhysRevLett.98.070401, arXiv:quant-ph/0608119]
-
Parsa Bonderson, Kirill Shtengel, Joost Slingerland, Interferometry of non-Abelian Anyons, Annals Phys. 323 (2008) 2709-2755 [doi:10.1016/j.aop.2008.01.012, arXiv:0707.4206]
-
Andrey Morozov, On measuring the topological charge of anyons [arXiv:2403.07847]
Anyonic topological order in terms of braided fusion categories
Claim and status
In condensed matter theory it is folklore that species of anyonic topological order correspond to braided unitary fusion categories/modular tensor categories.
The origin of the claim is:
- Alexei Kitaev, Section 8 and Appendix E of: Anyons in an exactly solved model and beyond, Annals of Physics 321 1 (2006) 2-111 doi:10.1016/j.aop.2005.10.005
Early accounts re-stating this claim (without attribution):
-
Chetan Nayak, Steven H. Simon, Ady Stern, Michael Freedman, Sankar Das Sarma, pp. 28 of: Non-Abelian Anyons and Topological Quantum Computation, Rev. Mod. Phys. 80 1083 (2008) arXiv:0707.1888, doi:10.1103/RevModPhys.80.1083
-
Zhenghan Wang, Section 6.3 of: Topological Quantum Computation, CBMS Regional Conference Series in Mathematics 112, AMS (2010) ISBN-13: 978-0-8218-4930-9, pdf
Further discussion (mostly review and mostly without attribution):
-
Simon Burton, A Short Guide to Anyons and Modular Functors arXiv:1610.05384
(this one stands out as still attributing the claim to Kitaev (2006), Appendix E)
-
Eric C. Rowell, Zhenghan Wang, Mathematics of Topological Quantum Computing, Bull. Amer. Math. Soc. 55 (2018), 183-238 (arXiv:1705.06206, doi:10.1090/bull/1605)
-
Tian Lan, A Classification of (2+1)D Topological Phases with Symmetries arXiv:1801.01210
-
From categories to anyons: a travelogue arXiv:1811.06670
-
Colleen Delaney, A categorical perspective on symmetry, topological order, and quantum information (2019) pdf, uc:5z384290
-
Colleen Delaney, Lecture notes on modular tensor categories and braid group representations (2019) pdf, pdf
-
Liang Wang, Zhenghan Wang, In and around Abelian anyon models, J. Phys. A: Math. Theor. 53 505203 (2020) doi:10.1088/1751-8121/abc6c0
-
Parsa Bonderson, Measuring Topological Order, Phys. Rev. Research 3, 033110 (2021) arXiv:2102.05677, doi:10.1103/PhysRevResearch.3.033110
-
Zhuan Li, Roger S.K. Mong, Detecting topological order from modular transformations of ground states on the torus arXiv:2203.04329
-
Eric C. Rowell, Braids, Motions and Topological Quantum Computing arXiv:2208.11762
-
Sachin Valera, A Quick Introduction to the Algebraic Theory of Anyons, talk at CQTS Initial Researcher Meeting (Sep 2022) pdf
-
Willie Aboumrad, Quantum computing with anyons: an F-matrix and braid calculator arXiv:2212.00831
Emphasis that the expected description of anyons by braided fusion categories had remained folklore, together with a list of minimal assumptions that would need to be shown:
- Sachin J. Valera, Fusion Structure from Exchange Symmetry in (2+1)-Dimensions, Annals of Physics 429 (2021)
An argument that the statement at least for SU(2)-anyons does follow from an enhancement of the K-theory classification of topological phases of matter to interacting topological order:
- Hisham Sati, Urs Schreiber, Anyonic topological order in TED K-theory, Rev. Math. Phys. (20223) arXiv:2206.13563, doi:10.1142/S0129055X23500010
Further discussion
Relation to ZX-calculus:
- Fatimah Rita Ahmadi, Aleks Kissinger, Topological Quantum Computation Through the Lens of Categorical Quantum Mechanics arXiv:2211.03855
On detection of topological order by observing modular transformations on the ground state:
- Zhuan Li, Roger S. K. Mong, Detecting topological order from modular transformations of ground states on the torus, Phys. Rev. B 106 (2022) 235115 doi:10.1103/PhysRevB.106.235115, arXiv:2203.04329
See also:
- Liang Kong, Topological Wick Rotation and Holographic Dualities, talk at CQTS (Oct 2022) pdf
Anyons in the quantum Hall liquids
References on anyon-excitations (satisfying braid group statistics) in the quantum Hall effect (for more on the application to topological quantum computation see the references there):
The prediction of abelian anyon-excitations in the quantum Hall effect (i.e. satisfying braid group statistics in 1-dimensional linear representations of the braid group):
-
B. I. Halperin, Statistics of Quasiparticles and the Hierarchy of Fractional Quantized Hall States, Phys. Rev. Lett. 52, 1583 (1984) (doi:10.1103/PhysRevLett.52.1583)
Erratum Phys. Rev. Lett. 52, 2390 (1984) (doi:10.1103/PhysRevLett.52.2390.4)
-
Daniel Arovas, J. R. Schrieffer, Frank Wilczek, Fractional Statistics and the Quantum Hall Effect, Phys. Rev. Lett. 53, 722 (1984) doi:10.1103/PhysRevLett.53.722
The original discussion of non-abelian anyon-excitations in the quantum Hall effect (i.e. satisfying braid group statistics in higher dimensional linear representations of the braid group, related to modular tensor categories):
- Gregory Moore, Nicholas Read, Nonabelions in the fractional quantum Hall effect, Nucl. Phys. 360B(1991)362 (pdf, doi:10.1016/0550-3213(91)90407-O)
Review:
- Ady Stern, Anyons and the quantum Hall effect – A pedagogical review, Annals of Physics Volume 323, Issue 1, January 2008, Pages 204-249 (doi:10.1016/j.aop.2007.10.008, arXiv:0711.4697)
Anyons in topological superconductors
On anyon-excitations in topological superconductors.
via Majorana zero modes:
Original proposal:
- Nicholas Read, Dmitry Green, Paired states of fermions in two dimensions with breaking of parity and time-reversal symmetries, and the fractional quantum Hall effect, Phys. Rev. B61:10267, 2000 (arXiv:cond-mat/9906453)
Review:
-
Sankar Das Sarma, Michael Freedman, Chetan Nayak, Majorana Zero Modes and Topological Quantum Computation, npj Quantum Information 1, 15001 (2015) (nature:npjqi20151)
-
Nur R. Ayukaryana, Mohammad H. Fauzi, Eddwi H. Hasdeo, The quest and hope of Majorana zero modes in topological superconductor for fault-tolerant quantum computing: an introductory overview (arXiv:2009.07764)
-
Yusuke Masaki, Takeshi Mizushima, Muneto Nitta, Non-Abelian Anyons and Non-Abelian Vortices in Topological Superconductors [arXiv:2301.11614]
Further developments:
-
Meng Cheng, Victor Galitski, Sankar Das Sarma, Non-adiabatic Effects in the Braiding of Non-Abelian Anyons in Topological Superconductors, Phys. Rev. B 84, 104529 (2011) (arXiv:1106.2549)
-
Javad Shabani et al., Two-dimensional epitaxial superconductor-semiconductor heterostructures: A platform for topological superconducting networks, Phys. Rev. B 93 155402 (2016) [doi:10.1103/PhysRevB.93.155402, arXiv:1511.01127]
-
Javad Shabani et al., Zero-Energy Modes from Coalescing Andreev States in a Two-Dimensional Semiconductor-Superconductor Hybrid Platform, Phys. Rev. Lett. 119 (2017) 176805 [doi:10.1103/PhysRevLett.119.176805, arXiv:1703.03699]
-
Javad Shabani et al., Fusion of Majorana Bound States with Mini-Gate Control in Two-Dimensional Systems, Nature Communications 13 (2022) 1738-1747 [doi:10.1038/s41467-022-29463-6, arXiv:2101.09272]
-
Javad Shabani et al., Quasiparticle dynamics in epitaxial Al-InAs planar Josephson junctions, PRX Quantum 4 030339 (2023) [doi:10.1103/PRXQuantum.4.030339, arXiv:2303.04784]
via Majorana zero modes restricted to edges of topological insulators:
- Biao Lian, Xiao-Qi Sun, Abolhassan Vaezi, Xiao-Liang Qi, and Shou-Cheng Zhang, Topological quantum computation based on chiral Majorana fermions, PNAS October 23, 2018 115 (43) 10938-10942; first published October 8, 2018 (doi:10.1073/pnas.1810003115)
See also:
- Yusuke Masaki, Takeshi Mizushima, Muneto Nitta, Non-Abelian Anyons and Non-Abelian Vortices in Topological Superconductors arXiv:2301.11614
Experimental detection of anyons
While the occurrence of anyon-excitations in the quantum Hall effect is a robust theoretical prediction (see the references above), and while the quantum Hall effect itself has long been established in experiment, the actual observation of anyons in these systems is subtle:
An early claim of the observation of non-abelian anyons seems to remain unconfirmed:
- Sanghun An, P. Jiang, H. Choi, W. Kang, S. H. Simon, L. N. Pfeiffer, K. W. West, K. W. Baldwin, Braiding of Abelian and Non-Abelian Anyons in the Fractional Quantum Hall Effect (arXiv:1112.3400)
The claimed observation of abelian anyons is apparently more securely established:
-
H. Bartolomei, M. Kumar, R. Bisognin, A. Marguerite, J.-M. Berroir, E. Bocquillon, B. Plaçais, A. Cavanna, Q. Dong, U. Gennser, Y. Jin, G. Fève:
Fractional statistics in anyon collisions, Science 368, 173-177 (2020) (arXiv:2006.13157)
-
James Nakamura, Shuang Liang, Geoffrey C. Gardner, Michael J. Manfra, Direct observation of anyonic braiding statistics, Nat. Phys. 16, 931–936 (2020). (arXiv:2006.14115, doi:10.1038/s41567-020-1019-1)
-
Bob Yirka, Best evidence yet for existence of anyons, PhysOrg News July 10, 2020 (phys.org/news/2020-07)
Defect anyons
Often the concept of anyons is introduced as if a generalization of perturbative quanta like fundamental bosons and fermions. But many (concepts of) types of anyons are really solitonicdefects such as vortices.
The general concept of braiding of defects in solid state physics:
-
N. David Mermin, The topological theory of defects in ordered media, Rev. Mod. Phys. 51 (1979) 591 doi:10.1103/RevModPhys.51.591
(including a review of basic homotopy theory)
and more specifically for vortices:
- Hoi-Kwong Lo, John Preskill, Non-Abelian vortices and non-Abelian statistics, Phys. Rev. D 48 (1993) 4821 doi:10.1103/PhysRevD.48.4821
Explicit discussion in terms of anyons:
-
Alexei Kitaev, Anyons in an exactly solved model and beyond, Annals of Physics 321 1 (2006) 2-111 doi:10.1016/j.aop.2005.10.005
Anyonic particles are best viewed as a kind of topological defects that reveal nontrivial properties of the ground state. p. 4
Concrete vortexanyons in Bose-Einstein condensates:
-
B. Paredes, P. Fedichev, J. I. Cirac, P. Zoller 1/2-Anyons in small atomic Bose-Einstein condensates, Phys. Rev. Lett. 87 (2001) 010402 arXiv:cond-mat/0103251, doi:10.1103/PhysRevLett.87.010402
-
Julien Garaud, Jin Dai, Antti J. Niemi, Vortex precession and exchange in a Bose-Einstein condensate, J. High Energ. Phys. 2021 157 (2021) arXiv:2010.04549
-
Thomas Mawson, Timothy Petersen, Joost Slingerland, Tapio Simula, Braiding and fusion of non-Abelian vortex anyons, Phys. Rev. Lett. 123 (2019) 140404 doi:10.1103/PhysRevLett.123.140404
and in (other) superfluids:
- Yusuke Masaki, Takeshi Mizushima, Muneto Nitta, Non-Abelian Half-Quantum Vortices in 3P2 Topological Superfluids arXiv:2107.02448
and in condensates of non-defect anyons:
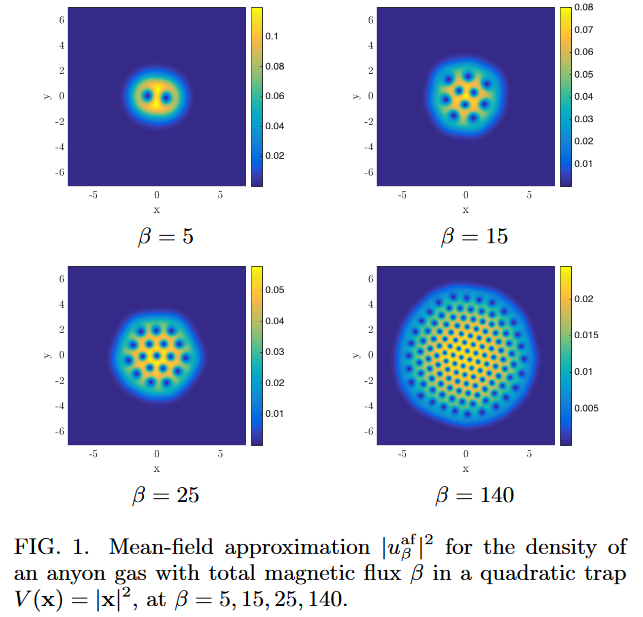
- Michele Correggi, Romain Duboscq, Douglas Lundholm, Nicolas Rougerie, Vortex patterns in the almost-bosonic anyon gas, Europhys. Lett. 126 (2019), 20005 arXiv:1901.10739, doi:10.1209/0295-5075/126/20005
See also Ahn, Park & Yang 19 who refer to the band nodes in the Brillouin torus of a semi-metal as “vortices in momentum space”.
And see at defect brane.
Anyons in momentum-space
On non-trivial braiding of nodal points in the Brillouin torus of topological semi-metals (“braiding in momentum space”):
-
Junyeong Ahn, Sungjoon Park, Bohm-Jung Yang, Failure of Nielsen-Ninomiya theorem and fragile topology in two-dimensional systems with space-time inversion symmetry: application to twisted bilayer graphene at magic angle, Phys. Rev. X 9 (2019) 021013 doi:10.1103/PhysRevX.9.021013, arXiv:1808.05375
“here are band crossing points, henceforth called vortices”
-
QuanSheng Wu, Alexey A. Soluyanov, Tomáš Bzdušek, Non-Abelian band topology in noninteracting metals, Science 365 (2019) 1273-1277 arXiv:1808.07469, doi:10.1126/science.aau8740
fundamental group of complement of nodal points/lines considered above (3)
-
Apoorv Tiwari, Tomáš Bzdušek, Non-Abelian topology of nodal-line rings in PT-symmetric systems, Phys. Rev. B 101 (2020) 195130 doi:10.1103/PhysRevB.101.195130
“a new type non-Abelian ‘braiding’ of nodal-line rings inside the momentum space”
- Adrien Bouhon, QuanSheng Wu, Robert-Jan Slager, Hongming Weng, Oleg V. Yazyev, Tomáš Bzdušek, Non-Abelian reciprocal braiding of Weyl points and its manifestation in ZrTe, Nature Physics 16 (2020) 1137-1143 arXiv:1907.10611, doi:10.1038/s41567-020-0967-9
“Here we report that Weyl points in three-dimensional (3D) systems with symmetry carry non-Abelian topological charges. These charges are transformed via non-trivial phase factors that arise upon braiding the nodes inside the reciprocal momentum space.”
Braiding of Dirac points in twisted bilayer graphene:
-
Jian Kang, Oskar Vafek, Non-Abelian Dirac node braiding and near-degeneracy of correlated phases at odd integer filling in magic angle twisted bilayer graphene, Phys. Rev. B 102 (2020) 035161 arXiv:2002.10360, doi:10.1103/PhysRevB.102.035161
-
Bin Jiang, Adrien Bouhon, Zhi-Kang Lin, Xiaoxi Zhou, Bo Hou, Feng Li, Robert-Jan Slager, Jian-Hua Jiang Experimental observation of non-Abelian topological acoustic semimetals and their phase transitions, Nature Physics 17 (2021) 1239-1246 arXiv:2104.13397, doi:10.1038/s41567-021-01340-x
(analog realization in phononic crystals)
Here, we consider an exotic type of topological phases beyond the above paradigms that, instead, depend on topological charge conversion processes when band nodes are braided with respect to each other in momentum space or recombined over the Brillouin zone. The braiding of band nodes is in some sense the reciprocal space analog of the non-Abelian braiding of particles in real space.
…
we experimentally observe non-Abelian topological semimetals and their evolutions using acoustic Bloch bands in kagome acoustic metamaterials. By tuning the geometry of the metamaterials, we experimentally confirm the creation, annihilation, moving, merging and splitting of the topological band nodes in multiple bandgaps and the associated non-Abelian topological phase transitions
-
Haedong Park, Stephan Wong, Xiao Zhang, and Sang Soon Oh, Non-Abelian Charged Nodal Links in a Dielectric Photonic Crystal, ACS Photonics 8 (2021) 2746–2754 [doi:10.1021/acsphotonics.1c00876]
-
Siyu Chen, Adrien Bouhon, Robert-Jan Slager, Bartomeu Monserrat, Non-Abelian braiding of Weyl nodes via symmetry-constrained phase transitions (formerly: Manipulation and braiding of Weyl nodes using symmetry-constrained phase transitions), Phys. Rev. B 105 (2022) L081117 arXiv:2108.10330, doi:10.1103/PhysRevB.105.L081117
“Our work opens up routes to readily manipulate Weyl nodes using only slight external parameter changes, paving the way for the practical realization of reciprocal space braiding.”
-
Bo Peng, Adrien Bouhon, Robert-Jan Slager, Bartomeu Monserrat, Multi-gap topology and non-Abelian braiding of phonons from first principles, Phys. Rev. B 105 (2022) 085115 (arXiv:2111.05872, doi:10.1103/PhysRevB.105.085115)
(analog realization in phononic crystals)
new opportunities for exploring non-Abelian braiding of band crossing points (nodes) in reciprocal space, providing an alternative to the real space braiding exploited by other strategies.
Real space braiding is practically constrained to boundary states, which has made experimental observation and manipulation difficult; instead, reciprocal space braiding occurs in the bulk states of the band structures and we demonstrate in this work that this provides a straightforward platform for non-Abelian braiding.
-
Bo Peng, Adrien Bouhon, Bartomeu Monserrat, Robert-Jan Slager, Phonons as a platform for non-Abelian braiding and its manifestation in layered silicates, Nature Communications 13 423 (2022) doi:10.1038/s41467-022-28046-9
(analog realization in phononic crystals)
it is possible to controllably braid Kagome band nodes in monolayer using strain and/or an external electric field.
-
Haedong Park, Wenlong Gao, Xiao Zhang, Sang Soon Oh, Nodal lines in momentum space: topological invariants and recent realizations in photonic and other systems, Nanophotonics 11 11 (2022) 2779–2801 doi:10.1515/nanoph-2021-0692
(analog realization in photonic crystals)
-
Adrien Bouhon, Robert-Jan Slager, Multi-gap topological conversion of Euler class via band-node braiding: minimal models, PT-linked nodal rings, and chiral heirs arXiv:2203.16741
See also:
-
Robert-Jan Slager, Adrien Bouhon, Fatma Nur Ünal, Floquet multi-gap topology: Non-Abelian braiding and anomalous Dirac string phase arXiv:2208.12824
-
Huahui Qiu et al., Minimal non-abelian nodal braiding in ideal metamaterials, Nature Communications 14 1261 (2023) doi:10.1038/s41467-023-36952-9
-
Wojciech J. Jankowski, Mohammedreza Noormandipour, Adrien Bouhon, Robert-Jan Slager, Disorder-induced topological quantum phase transitions in Euler semimetals arXiv:2306.13084
Incidentally, references indicating that the required toroidal (or yet higher genus) geometry for anyonic topological order in position space is dubious (as opposed to the evident toroidal geometry of the momentum-space Brillouin torus): Lan 19, p. 1, ….
Knotted nodal lines in 3d semimetals
Beware that various authors consider braids/knots formed by nodal lines in 3d semimetals, i.e. knotted nodal lines in 3 spatial dimensions, as opposed to worldlines (in 2+1 spacetime dimensions) of nodal points in effectively 2d semimetals needed for the anyon-braiding considered above.
An argument that these nodal lines in 3d space, nevertheless, may be controlled by Chern-Simons theory:
- Biao Lian, Cumrun Vafa, Farzan Vafa, Shou-Cheng Zhang, Chern-Simons theory and Wilson loops in the Brillouin zone, Phys. Rev. B 95 (2017) 094512 [doi:10.1103/PhysRevB.95.094512]
Topological quantum computation with anyons
The idea of topological quantum computation via a Chern-Simons theory with anyon braiding defects is due to:
-
Alexei Kitaev, Fault-tolerant quantum computation by anyons, Annals Phys. 303 (2003) 2-30 arXiv:quant-ph/9707021, doi:10.1016/S0003-4916(02)00018-0
-
Michael Freedman, P/NP, and the quantum field computer, Proc. Nat. Acad. Sci. 95 1 (1998) 98-101 doi:10.1073/pnas.95.1.9
-
Michael Freedman, Alexei Kitaev, Michael Larsen, Zhenghan Wang, Topological quantum computation, Bull. Amer. Math. Soc. 40 (2003), 31-38 (arXiv:quant-ph/0101025, doi:10.1090/S0273-0979-02-00964-3, pdf)
-
Michael Freedman, Michael Larsen, Zhenghan Wang, A modular functor which is universal for quantum computation, Communications in Mathematical Physics. 227 3 (2002) 605-622 arXiv:quant-ph/0001108, doi:10.1007/s002200200645
(specifically via su(2)-anyons)
-
Chetan Nayak, Steven H. Simon, Ady Stern, Michael Freedman, Sankar Das Sarma, Non-Abelian Anyons and Topological Quantum Computation, Rev. Mod. Phys. 80 1083 (2008) arXiv:0707.1888, doi:10.1103/RevModPhys.80.1083
-
Dmitry Melnikov, Andrei Mironov, Sergey Mironov, Alexei Morozov, Andrey Morozov, Towards topological quantum computer, Nucl. Phys. B926 (2018) 491-508 (arXiv:1703.00431, doi:10.1016/j.nuclphysb.2017.11.016)
and via a Dijkgraaf-Witten theory (like Chern-Simons theory but with discrete gauge group):
-
R. Walter Ogburn, John Preskill, Topological Quantum Computation, in: Quantum Computing and Quantum Communications, Lecture Notes in Computer Science 1509, Springer (1998) doi:10.1007/3-540-49208-9_31
-
Carlos Mochon, Anyons from non-solvable finite groups are sufficient for universal quantum computation, Phys. Rev. A 67 022315 (2003) arXiv:quant-ph/0206128, doi:10.1103/PhysRevA.67.022315
-
Carlos Mochon, Anyon computers with smaller groups, Phys. Rev. A 69 032306 (2004) arXiv:quant-ph/0306063, doi:10.1103/PhysRevA.69.032306
Textbook accounts:
-
Zhenghan Wang, Topological Quantum Computation, CBMS Regional Conference Series in Mathematics 112, AMS 2010 (ISBN-13: 978-0-8218-4930-9, pdf)
-
Jiannis K. Pachos, Introduction to Topological Quantum Computation, Cambridge University Press (2012) doi:10.1017/CBO9780511792908
-
Tudor D. Stanescu, Part IV of: Introduction to Topological Quantum Matter & Quantum Computation, CRC Press 2020 (ISBN:9780367574116)
-
Steven H. Simon, Topological Quantum, 2021 pdf, webpage
Review:
-
Louis Kauffman, Quantum Topology and Quantum Computing, in: Samuel J. Lomonaco (ed.), Quantum Computation: A Grand Mathematical Challenge for the Twenty-First Century and the Millennium, Proceedings of Symposia in Applied Mathematics 58, AMS (2002) [pdf, doi:10.1090/psapm/058]
(in relation to quantum topology)
-
Gavin K. Brennen, Jiannis K. Pachos, Why should anyone care about computing with anyons?, Proc. R. Soc. A 464 (2008) 1-24 arXiv:0704.2241, doi:10.1098/rspa.2007.0026
-
Ady Stern, Netanel H. Lindner, Topological Quantum Computation – From Basic Concepts to First Experiments, Science 339 6124 (2013) 1179-1184 (doi:10.1126/science.1231473)
-
Eric C. Rowell, An Invitation to the Mathematics of Topological Quantum Computation, J. Phys.: Conf. Ser. 698 (2016) 012012 (doi:10.1088/1742-6596/698/1/012012)
-
Ananda Roy, David P. DiVincenzo, Topological Quantum Computing, Lecture notes of the 48th IFF Spring School (2017) arXiv:1701.05052
-
Ville Lahtinen, Jiannis K. Pachos, A Short Introduction to Topological Quantum Computation, SciPost Phys. 3 021 (2017) arXiv:1705.04103, doi:10.21468/SciPostPhys.3.3.021
-
Eric C. Rowell, Zhenghan Wang, Mathematics of Topological Quantum Computing, Bull. Amer. Math. Soc. 55 (2018), 183-238 (arXiv:1705.06206, doi:10.1090/bull/1605)
-
Bernard Field, Tapio Simula, Introduction to topological quantum computation with non-Abelian anyons, Quantum Science and Technology 3 (2018) 045004 arXiv:1802.06176, doi:10.1088/2058-9565/aacad2
-
Muhammad Ilyas, Quantum Field Theories, Topological Materials, and Topological Quantum Computing arXiv:2208.09707
-
Eric C. Rowell, Braids, Motions and Topological Quantum Computing arXiv:2208.11762
Focus on abelian anyons:
-
Jiannis K. Pachos, Quantum computation with abelian anyons on the honeycomb lattice, International Journal of Quantum Information 4 6 (2006) 947-954 (arXiv:quant-ph/0511273)
-
James Robin Wootton, Dissecting Topological Quantum Computation, 2010 (pdf, pdf)
“non-Abelian anyons are usually assumed to be better suited to the task. Here we challenge this view, demonstrating that Abelian anyon models have as much potential as some simple non-Abelian models.”
-
Wade Bloomquist, Zhenghan Wang, On Topological Quantum Computing With Mapping Class Group Representations, J. Phys. A: Math. Theor. 52 (2019) 015301 (arXiv:1805.04622, doi:10.1088/1751-8121/aaeea1)
-
Seth Lloyd, Quantum computation with abelian anyons, Quantum Information Processing 1 1/2 (2002) (arXiv:quant-ph/0004010, doi:10.1023/A:1019649101654)
Realization in experiment:
-
Daniel Nigg, Markus Mueller, Esteban A. Martinez, Philipp Schindler, Markus Hennrich, Thomas Monz, Miguel A. Martin-Delgado, Rainer Blatt,
Experimental Quantum Computations on a Topologically Encoded Qubit, Science 18 Jul 2014: Vol. 345, Issue 6194, pp. 302-305 (arXiv:1403.5426, doi:10.1126/science.1253742)
(for quantum error correction)
Simulation of Ising anyons in a lattice of ordinary superconducting qbits:
- T. Andersen et al. Observation of non-Abelian exchange statistics on a superconducting processor arXiv:2210.10255
Braid group representations (as topological quantum gates)
On linear representations of braid groups (see also at braid group statistics and interpretation as quantum gates in topological quantum computation):
- Ivan Marin, On the representation theory of braid groups, Annales mathématiques Blaise Pascal, 20 2 (2013) 193-260 (arXiv:math/0502118, dml:275607)
Review:
-
Chen Ning Yang, M. L. Ge (eds.). Braid Group, Knot Theory and Statistical Mechanics, Advanced Series in Mathematical Physics 9, World Scientific (1991) doi:10.1142/0796
(focus on quantum Yang-Baxter equation)
-
Camilo Arias Abad, Introduction to representations of braid groups, Rev. colomb. mat. vol.49 no.1 (2015) (arXiv:1404.0724, doi:10.15446/recolma.v49n1.54160)
-
Toshitake Kohno, Introduction to representation theory of braid groups, Peking 2018 (pdf, pdf)
in relation to modular tensor categories:
- Colleen Delaney, Lecture notes on modular tensor categories and braid group representations, 2019 (pdf, pdf)
Braid representations from the monodromy of the Knizhnik-Zamolodchikov connection on bundles of conformal blocks over configuration spaces of points:
-
Ivan Todorov, Ludmil Hadjiivanov, Monodromy Representations of the Braid Group, Phys. Atom. Nucl. 64 (2001) 2059-2068; Yad.Fiz. 64 (2001) 2149-2158 arXiv:hep-th/0012099, doi:10.1134/1.1432899
-
Ivan Marin, Sur les représentations de Krammer génériques, Annales de l’Institut Fourier, 57 6 (2007) 1883-1925 numdam:AIF_2007__57_6_1883_0
and understood in terms of anyon statistics:
- Xia Gu, Babak Haghighat, Yihua Liu, Ising- and Fibonacci-Anyons from KZ-equations, J. High Energ. Phys. 2022 15 (2022) [doi:10.1007/JHEP09(2022)015, arXiv:2112.07195]
Braid representations seen inside the topological K-theory of the braid group‘s classifying space:
-
Alejandro Adem, Daniel C. Cohen, Frederick R. Cohen, On representations and K-theory of the braid groups, Math. Ann. 326 (2003) 515-542 (arXiv:math/0110138, doi:10.1007/s00208-003-0435-8)
-
Frederick R. Cohen, Section 3 of: On braid groups, homotopy groups, and modular forms, in: J.M. Bryden (ed.), Advances in Topological Quantum Field Theory, Kluwer 2004, 275–288 (pdf)
See also:
- R. B. Zhang, Braid group representations arising from quantum supergroups with arbitrary and link polynomials, Journal of Mathematical Physics 33, 3918 (1992) (doi:10.1063/1.529840)
As quantum gates for topological quantum computation with anyons:
-
Louis H. Kauffman, Samuel J. Lomonaco, Braiding Operators are Universal Quantum Gates, New Journal of Physics, Volume 6, January 2004 (arXiv:quant-ph/0401090, doi:10.1088/1367-2630/6/1/134)
-
Samuel J. Lomonaco, Louis Kauffman, Topological Quantum Computing and the Jones Polynomial, Proc. SPIE 6244, Quantum Information and Computation IV, 62440Z (2006) (arXiv:quant-ph/0605004)
(braid group representation serving as a topological quantum gate to compute the Jones polynomial)
-
Louis H. Kauffman, Samuel J. Lomonaco, Topological quantum computing and braid group representations, Proceedings Volume 6976, Quantum Information and Computation VI; 69760M (2008) (doi:10.1117/12.778068, rg:228451452)
-
C.-L. Ho, A.I. Solomon, C.-H.Oh, Quantum entanglement, unitary braid representation and Temperley-Lieb algebra, EPL 92 (2010) 30002 (arXiv:1011.6229)
-
Louis H. Kauffman, Majorana Fermions and Representations of the Braid Group, International Journal of Modern Physics AVol. 33, No. 23, 1830023 (2018) (arXiv:1710.04650, doi:10.1142/S0217751X18300235)
-
David Lovitz, Universal Braiding Quantum Gates [arXiv:2304.00710]
Introduction and review:
-
Colleen Delaney, Eric C. Rowell, Zhenghan Wang, Local unitary representations of the braid group and their applications to quantum computing, Revista Colombiana de Matemáticas(2017), 50 (2):211 (arXiv:1604.06429, doi:10.15446/recolma.v50n2.62211)
-
Eric C. Rowell, Braids, Motions and Topological Quantum Computing arXiv:2208.11762
Realization of Fibonacci anyons on quasicrystal-states:
- Marcelo Amaral, David Chester, Fang Fang, Klee Irwin, Exploiting Anyonic Behavior of Quasicrystals for Topological Quantum Computing, Symmetry 14 9 (2022) 1780 arXiv:2207.08928, doi:10.3390/sym14091780
Realization on supersymmetric spin chains:
- Indrajit Jana, Filippo Montorsi, Pramod Padmanabhan, Diego Trancanelli, Topological Quantum Computation on Supersymmetric Spin Chains arXiv:2209.03822
See also:
- Yuanjie Ren, Peter Shor, Topological quantum computation assisted by phase transitions [arXiv:2311.00103]
Compilation to braid gate circuits
On approximating (cf. the Solovay-Kitaev theorem) given quantum gates by (i.e. compiling them to) cicuits of anyon braid gates (generally considered for su(2)-anyons and here mostly for universal Fibonacci anyons, to some extent also for non-universal Majorana anyons):
-
Nicholas E. Bonesteel, Layla Hormozi, Georgios Zikos, Steven H. Simon, Braid Topologies for Quantum Computation, Phys. Rev. Lett. 95 140503 (2005) arXiv:quant-ph/0505065, doi:10.1103/PhysRevLett.95.140503
-
Layla Hormozi, Georgios Zikos, Nicholas E. Bonesteel, Steven H. Simon, Topological Quantum Compiling, Phys. Rev. B 75 165310 (2007) arXiv:quant-ph/0610111, doi:10.1103/PhysRevB.75.165310
-
Layla Hormozi, Nicholas E. Bonesteel, Steven H. Simon, Topological Quantum Computing with Read-Rezayi States, Phys. Rev. Lett. 103 160501 (2009) doi:10.1103/PhysRevLett.103.160501, arXiv:0903.2239
-
M. Baraban, Nicholas E. Bonesteel, Steven H. Simon, Resources required for topological quantum factoring, Phys. Rev. A 81 062317 (2010) doi:10.1103/PhysRevA.81.062317, arXiv:1002.0537
(focus on compiling Shor's algorithm)
-
Vadym Kliuchnikov, Alex Bocharov, Krysta M. Svore, Asymptotically Optimal Topological Quantum Compiling, Phys. Rev. Lett. 112 140504 (2014) arXiv:1310.4150, journal: doi:10.1103/PhysRevLett.112.140504, talk recording: doi:10.48660/13100129
-
Joren W. Brunekreef, Topological Quantum Computation and Quantum Compilation, Utrecht (2014) studenttheses.uu.nl:20.500.12932/17738
-
Yuan-Hang Zhang, Pei-Lin Zheng, Yi Zhang, Dong-Ling Deng, Topological Quantum Compiling with Reinforcement Learning, Phys. Rev. Lett. 125 170501 (2020) doi:2004.04743, doi:10.1103/PhysRevLett.125.170501
-
Emil Génetay-Johansen, Tapio Simula, Section IV of: Fibonacci anyons versus Majorana fermions – A Monte Carlo Approach to the Compilation of Braid Circuits in Anyon Models, PRX Quantum 2 010334 (2021) arXiv:2008.10790, doi:10.1103/PRXQuantum.2.010334
-
Cheng-Qian Xu, D. L. Zhou, Quantum teleportation using Ising anyons, Phys. Rev. A 106 012413 (2022) arXiv:2201.11923, doi:10.1103/PhysRevA.106.012413
(focus on implemening the quantum teleportation-protocol with Ising anyons)
Approximating all topological quantum gates by just the weaves among all braids:
-
Steven H. Simon, Nick E. Bonesteel, Michael H. Freedman, N. Petrovic, Layla Hormozi, Topological Quantum Computing with Only One Mobile Quasiparticle, Phys. Rev. Lett. 96 (2006) 070503 (arXiv:quant-ph/0509175, doi:10.1103/PhysRevLett.96.070503)
-
Layla Hormozi, Georgios Zikos, Nick E. Bonesteel, Steven H. Simon, Topological quantum compiling, Phys. Rev. B 75, 165310 (doi:10.1103/PhysRevB.75.165310, arXiv:quant-ph/0610111)
-
Mohamed Taha Rouabah, Compiling single-qubit braiding gate for Fibonacci anyons topological quantum computation (arXiv:2008.03542)
Last revised on March 14, 2024 at 05:20:02. See the history of this page for a list of all contributions to it.