nLab Riemannian orbifold
Context
Riemannian geometry
Higher geometry
higher geometry / derived geometry
Ingredients
Concepts
-
geometric little (∞,1)-toposes
-
geometric big (∞,1)-toposes
Constructions
Examples
-
derived smooth geometry
Theorems
Contents
Idea
The concept of Riemannian orbifolds is the joint generalization of the concepts of Riemannian manifolds and orbifolds:
A Riemannian orbifold is an orbifold equipped with an orbifold atlas where each chart is equipped with a Riemannian metric such that the action of is by isometries, and such that the transition functions from one chart to the other are isometries.
A key aspect is that the orbifold singularities behave like carrying singular curvature, notably there are flat orbifolds (also “Euclidean orbifolds”, i.e. Riemannian orbifolds with vanishing Riemann curvature away from the singularities) whose underlying topological spaces are n-spheres (see below).
Key examples of flat orbifolds are global homotopy quotients of the n-torus equipped with its canonical flat Riemannian metric. These flat orbifolds are called toroidal orbifolds.
Properties
under construction
Every flat orbifold whose underlying metric space is connected and complete) is a global quotient of Euclidean space/Cartesian space
Examples
Non-compact orbifolds
Basic examples of non-compact Riemannian orbifolds are conical singularities.
In the flat case these are homotopy quotients of the form for a finite group and a finite-dimensional orthogonal linear representation of .
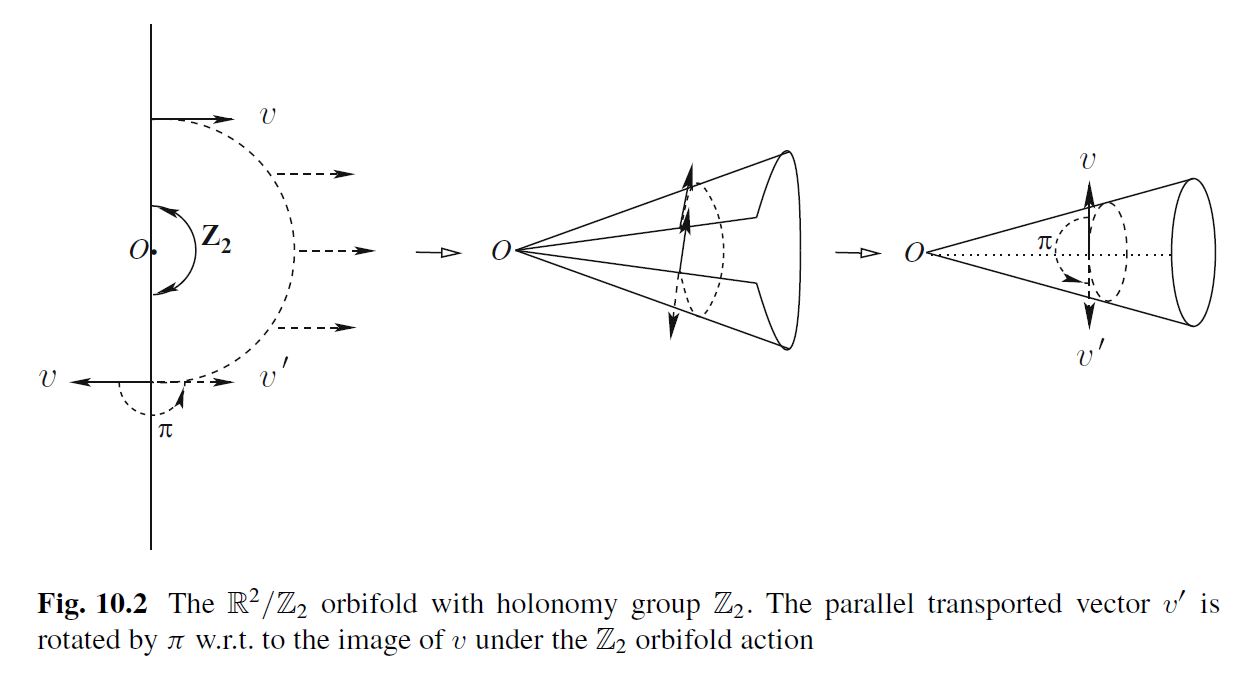
graphics grabbed from Blumenhagen-Lüst-Theisen 13
For equipped with the canonical action of finite subgroups of SU(2) these are the ADE-singularities.
Compact flat orbifolds from crystallographic groups
Example
(compact flat orbifolds from crystallographic groups)
Let be a Euclidean space and a crystallographic group acting on it, with translational normal subgroup lattice and corresponding point group .
Then the action of on descends to the quotient space torus (this Prop.)
The resulting homotopy quotient is a compact flat orbifold.
The following is the class of special cases of Example for point group being the involution-action by reflection at a point:
Example
(coordinate reflection on n-torus)
Let be the d-torus and consider the action of the cyclic group by canonical coordinate reflection
The resulting homotopy quotient orbifold has singularities/fixed points, namely the points with all coordinates in .
In applications to string theory orbifolds of the form play the role of orientifold spacetimes with Op-planes.
Flat compact 2-dimensional orbifolds
In 2 dimensions the crystallographic groups are the “wallpaper groups”. Hence, as a special case of Example , the flat compact 2-dimensional orbifolds may be classified as homotopy quotients of the 2-torus by wallpaper groups (for review see e.g. Guerreiro 09):
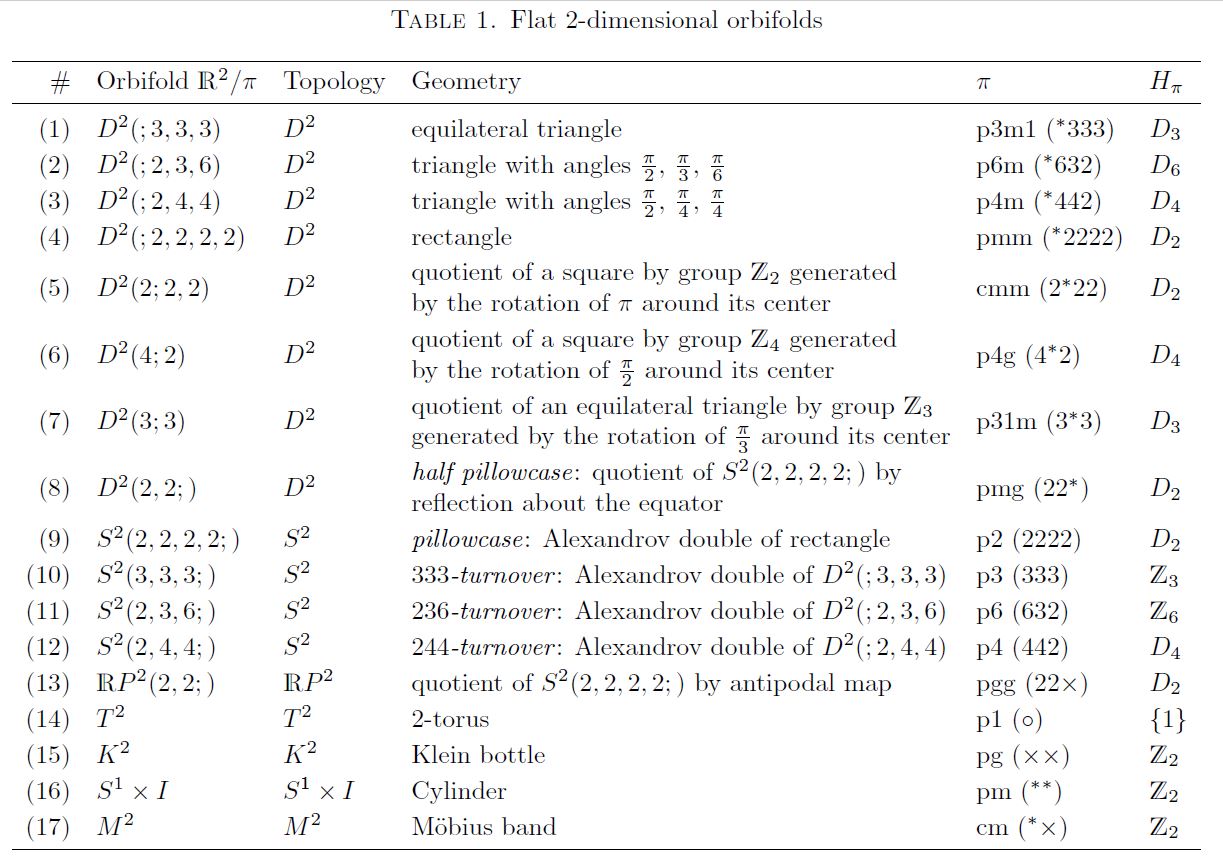
graphics grabbed from Bettiol-Derdzinski-Piccione 18
2-sphere
The 2-sphere arises, in particular, as the quotient space of the torus by the involution , exhibited by the Weierstrass elliptic function (e.g. Mukase 04, end of 1.4. This realizes the 2-sphere as the underlying coarse space of a flat orbifold with four singular points, called the pillowcase orbifold.
Flat compact 3-dimensional orbifolds
3-Sphere
Many flat compact oriented 3-dimensional orbifolds have coarse underlying topological space the 3-sphere (Dunbar 88)
Flat compact 4-dimensional orbifolds
Kummer surface
The orbifold quotient of the 4-torus by the sign involution on all four canonical coordinates is the flat compact 4-dimensional orbifold known as the Kummer surface – the special case of Example for . This is a singular K3-surface (e.g. Bettiol-Derdzinski-Piccione 18, 5.5)

graphics grabbed from Snowden 11
Also gives a toroidal orbifold. As orientifolds with D5-branes in type IIB string theory these are discussed in Buchel-Shiu-Tye 99, Sec. II.
4-Sphere
The complex projective space is an orbifold quotient of the 4-torus (see this MO comment), in generalization of how the Weierstrass elliptic function exhibits the Riemann sphere as (above).
A further -quotient of gives the 4-sphere (see at 4-sphere as quotient of complex projective plane).
Flat compact 6-dimensional orbifolds
see FRTV 12
7-Dimensional -orbifolds
see G2-orbifold
Related concepts
References
General
-
Joseph Ernest Borzellino, Riemannian Geometry of Orbifolds, Dissertation, University of California - Los Angeles, January 1, 1992, pages 1-57. 1992 (calpoly.edu/math_fac/111)
-
John Ratcliffe, Geometric Orbifolds, chapter 13 in Foundations of Hyperbolic Manifolds, Graduate Texts in Mathematics 149, Springer 2006 (doi:10.1007/978-0-387-47322-2, pdf)
-
Christian Lange, Orbifolds from a metric viewpoint, Geom Dedicata (2020) (arXiv:1801.03472, doi:10.1007/s10711-020-00521-x)
-
Renato G. Bettiol, Andrzej Derdzinski, Paolo Piccione, Teichmüller theory and collapse of flat manifolds, Annali di Matematica 197 (2018) 1247-1268 [arXiv:1705.08431, doi:10.1007/s10231-017-0723-7]
The isometry group of Riemannian orbifolds:
- A. V. Bagaev & N. I. Zhukova, The isometry groups of Riemannian orbifolds, Sib Math J 48, 579–592 (2007) (doi:10.1007/s11202-007-0060-y)
Real-analytic Riemannian orbifolds:
- Marja Kankaanrinta, On real analytic orbifolds and Riemannian metrics, Algebraic & Geometric Topology 13 (2013) 2369–2381 (doi:10.2140/agt.2013.13.2369)
The Yamabe invariant:
- Kazuo Akutagawal, Computations of the orbifold Yamabe invariant, Mathematische Zeitschrift volume 271, pages 611–625 (2012) (doi:10.1007/s00209-011-0880-0)
More generally, G-structures on orbifolds:
-
A. V. Bagaev, N. I. Zhukova , The Automorphism Groups of Finite Type -Structures on Orbifolds, Siberian Mathematical Journal 44, 213–224 (2003) (doi:10.1023/A:1022920417785)
-
Robert Wolak, Orbifolds, geometric structures and foliations. Applications to harmonic maps, Rendiconti del seminario matematico - Universita politecnico di Torino, vol. 73/1 , 3-4 (2016), 173-187 (arXiv:1605.04190)
Discussion of gravity and maybe quantum gravity on orbifolds:
- Helio V. Fagundes, Teofilo Vargas, Orbifolds, Quantum Cosmology, and Nontrivial Topology (arXiv:gr-qc/0611048)
Discussion of perturbative string theory on toroidal orbifolds
- Ralph Blumenhagen, Dieter Lüst, Stefan Theisen, Chapter 10.5 Toroidal orbifolds, of Basic Concepts of String Theory Part of the series Theoretical and Mathematical Physics pp 585-639 Springer 2013
For more see the references at orbifold.
Flat orbifolds
- John Ratcliffe, Steven T. Tschantz, The Calabi construction for compact flat orbifolds, Topology and its Applications Volume 178, 1 December 2014, Pages 87-106 (doi:10.1016/j.topol.2014.09.005)
Of dimension 2
In 2 dimensions
-
John Milnor, On Lattès Maps (arXiv:math/0402147)
-
João Guerreiro, Orbifolds and Wallpaper Patterns (pdf)
2d toroidal orientifolds:
-
Dongfeng Gao, Kentaro Hori, Section 7.3 of: On The Structure Of The Chan-Paton Factors For D-Branes In Type II Orientifolds (arXiv:1004.3972)
-
Charles Doran, Stefan Mendez-Diez, Jonathan Rosenberg, String theory on elliptic curve orientifolds and KR-theory (arXiv:1402.4885)
Of dimension 3
- William Dunbar, Geometric orbifolds, Rev. Mat. Univ. Complutense Madr. 1, No.1-3, 67-99 (1988)
Of dimension 4
Flat (toroidal) orbifolds of dimension 4:
In the the context of black holes in string theory:
- Justin R. David, Gautam Mandal, Spenta R. Wadia, Microscopic Formulation of Black Holes in String Theory, Phys.Rept.369:549-686,2002 (arXiv:hep-th/0203048)
In the context of RR-field tadpole cancellation for intersecting D-brane models on toroidal orientifolds:
Specifically K3 orientifolds () in type IIB string theory, hence for D9-branes and D5-branes:
-
Eric Gimon, Joseph Polchinski, Section 3.2 of: Consistency Conditions for Orientifolds and D-Manifolds, Phys. Rev. D54: 1667-1676, 1996 (arXiv:hep-th/9601038)
-
Eric Gimon, Clifford Johnson, K3 Orientifolds, Nucl. Phys. B477: 715-745, 1996 (arXiv:hep-th/9604129)
-
Alex Buchel, Gary Shiu, S.-H. Henry Tye, Anomaly Cancelations in Orientifolds with Quantized B Flux, Nucl.Phys. B569 (2000) 329-361 (arXiv:hep-th/9907203)
-
P. Anastasopoulos, A. B. Hammou, A Classification of Toroidal Orientifold Models, Nucl. Phys. B729:49-78, 2005 (arXiv:hep-th/0503044)
Specifically K3 orientifolds () in type IIA string theory, hence for D8-branes and D4-branes:
-
Jaemo Park, Angel Uranga, A Note on Superconformal N=2 theories and Orientifolds, Nucl. Phys. B542:139-156, 1999 (arXiv:hep-th/9808161)
-
G. Aldazabal, S. Franco, Luis Ibanez, R. Rabadan, Angel Uranga, D=4 Chiral String Compactifications from Intersecting Branes, J. Math. Phys. 42:3103-3126, 2001 (arXiv:hep-th/0011073)
-
G. Aldazabal, S. Franco, Luis Ibanez, R. Rabadan, Angel Uranga, Intersecting Brane Worlds, JHEP 0102:047, 2001 (arXiv:hep-ph/0011132)
-
H. Kataoka, M. Shimojo, Chiral Models from Intersecting D4-/D5-branes, Progress of Theoretical Physics, Volume 107, Issue 6, June 2002, Pages 1291–1296 (arXiv:hep-th/0112247, doi:10.1143/PTP.107.1291)
Systematic construction of Ricci flat Riemannian metrics on K3 orbifolds:
-
Shamit Kachru, Arnav Tripathy, Max Zimet, K3 metrics (arXiv:2006.02435)
-
Arnav Tripathy, Max Zimet, A plethora of K3 metrics (arXiv:2010.12581)
In the context of Mathieu moonshine from string sigma models on K3s:
-
Matthias Gaberdiel, Stefan Hohenegger, Roberto Volpato, Symmetries of K3 sigma models, Commun.Num.Theor.Phys. 6 (2012) 1-50 (arXiv:1106.4315)
-
Matthias Gaberdiel, Roberto Volpato, Mathieu Moonshine and Orbifold K3s (arXiv:1206.5143)
Of dimension 6
In 6 dimensions (mostly motivated as singular Calabi-Yau compactifications of heterotic string theory to 4d)
-
Jens Erler, Albrecht Klemm, Comment on the Generation Number in Orbifold Compactifications, Commun. Math. Phys. 153:579-604, 1993 (arXiv:hep-th/9207111)
-
Dieter Lüst, S. Reffert, E. Scheidegger, S. Stieberger, Resolved Toroidal Orbifolds and their Orientifolds, Adv. Theor. Math. Phys. 12:67-183, 2008 (arXiv:hep-th/0609014)
-
S. Reffert, Toroidal Orbifolds: Resolutions, Orientifolds and Applications in String Phenomenology, Munich 2006 (arXiv:hep-th/0609040, spire:725406)
-
Ron Donagi, Katrin Wendland, On orbifolds and free fermion constructions, J. Geom. Phys. 59:942-968, 2009 (arXiv:0809.0330)
-
Maximilian Fischer, Michael Ratz, Jesus Torrado, Patrick K.S. Vaudrevange, Classification of symmetric toroidal orbifolds, JHEP 1301 (2013) 084 (arXiv:1209.3906)
Last revised on March 16, 2024 at 21:17:14. See the history of this page for a list of all contributions to it.