nLab Gromoll-Meyer sphere

Idea

What is called the Gromoll-Meyer sphere (Gromoll-Meyer 74) is an example of an exotic 7-sphere. It arises as a double coset space/biquotient of the quaternionic unitary group Sp(2) $\simeq$ Spin(5) by two copies of Sp(1) $\simeq$ SU(2).

Definition

Consider the quaternion unitary group Sp(2) $\simeq$ Spin(5) and its two subgroup inclusion of Sp(1) $\simeq$ SU(2) as

$$Sp(1) \;\simeq\; \left\{ \left( \array{ q & 0 \\ 0 & q } \right) \;\vert\; q \in Sp(1) \right\} \phantom{AA} \text{and} \phantom{AA} Sp(1) \;\simeq\; \left\{ \left( \array{ q & 0 \\ 0 & 1 } \right) \;\vert\; q \in Sp(1) \right\}$$

Then the double coset space/biquotient $Sp(1)\backslash Sp(2) /Sp(1)$ with respect to the left and right multiplication action, respectively, of these two subgroups is, with respect to its canonically induced geometric structures:

1. homeomorphic to the topological 7-sphere;

2. diffeomorphic to an exotic 7-sphere.

As such, it is called the Gromoll-Meyer sphere, due to Gromoll-Meyer 74

$$Sp(1)\backslash Sp(2) /Sp(1) \;\simeq\; S^7_{exotic}$$

Properties

• The Gromoll-Meyer sphere is the only exotic 7-sphere that can be modeled by a biquotient of a compact Lie group (KZ02, Corollary C).

• The Gromoll-Meyer sphere is a 3-sphere-bundle over the 4-sphere.

• It is a generator of the group of diffeomorphism classes of oriented homotopy spheres in dimension 7, which is of order 28.

Related concepts

coset space-structures on n-spheres:

standard:
$S^{n-1} \simeq_{diff} SO(n)/SO(n-1)$	this Prop.
$S^{2n-1} \simeq_{diff} SU(n)/SU(n-1)$	this Prop.
$S^{4n-1} \simeq_{diff} Sp(n)/Sp(n-1)$	this Prop.
exceptional:
$S^7 \simeq_{diff} Spin(7)/G_2$	Spin(7)/G₂ is the 7-sphere
$S^7 \simeq_{diff} Spin(6)/SU(3)$	since Spin(6) $\simeq$ SU(4)
$S^7 \simeq_{diff} Spin(5)/SU(2)$	since Sp(2) is Spin(5) and Sp(1) is SU(2), see Spin(5)/SU(2) is the 7-sphere
$S^6 \simeq_{diff} G_2/SU(3)$	G₂/SU(3) is the 6-sphere
$S^15 \simeq_{diff} Spin(9)/Spin(7)$	Spin(9)/Spin(7) is the 15-sphere

see also Spin(8)-subgroups and reductions

homotopy fibers of homotopy pullbacks of classifying spaces:

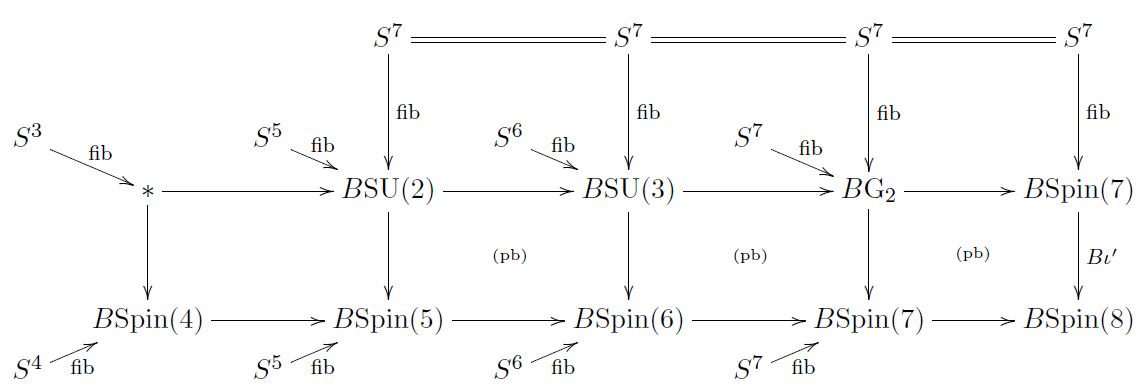
(from FSS 19, 3.4)

References

The construction is due to

• Detlef Gromoll, Wolfgang Meyer, An Exotic Sphere With Nonnegative Sectional Curvature, Annals of Mathematics Second Series, Vol. 100, No. 2 (Sep., 1974), pp. 401-406 (jstor:1971078)

Review includes

• Michael Joachim, D. J. Wraith, pages 7-8 of Exotic spheres and curvature (pdf)

Generalization of the construction to a large class of exotic 7-spheres:

• C. Duran, T. Puettmann, A. Rigas, An infinite family of Gromoll-Meyer spheres. Arch. Math. (2010) 95: 269 (arXiv:math/0610349, doi:10.1007/s00013-010-0161-x)

See also:

• Jost-Hinrich Eschenburg, Martin Kerin, Almost positive curvature on the Gromoll-Meyer sphere, Proc. Amer. Math. Soc (arXiv:0711.2987)

• Carlos Durán, Thomas Püttmann, A minimal Brieskorn 5-sphere in the Gromoll-Meyer sphere and its applications, Michigan Math. J. Volume 56, Issue 2 (2008), 419-451 (euclid)

• Llohann D. Sperança, Pulling back the Gromoll-Meyer construction and models of exotic spheres, Proceedings of the American Mathematical Society 144.7 (2016): 3181-3196 (arXiv:1010.6039)

• Llohann D. Sperança, Explicit Constructions over the Exotic 8-sphere (pdf, pdf)

• David S. Berman, Martin Cederwall, Tancredi Schettini Gherardini: Curvature of an exotic 7-sphere [arXiv:2410.01909]

For a proof that the Gromoll-Meyer sphere is the only exotic sphere that is a biquotient of a compact Lie group see

• Vitali Kapovitch, Wolfgang Ziller, Biquotients with singly generated rational cohomology, (arXiv:math/0210231)