nLab Cayley graph
Context
Group Theory
- group, ∞-group
- group object, group object in an (∞,1)-category
- abelian group, spectrum
- super abelian group
- group action, ∞-action
- representation, ∞-representation
- progroup
- homogeneous space
Classical groups
Finite groups
Group schemes
Topological groups
Lie groups
Super-Lie groups
Higher groups
Cohomology and Extensions
Related concepts
Contents
Idea
In geometric group theory, the Cayley graph (also: Cayley quiver) of a group, , equipped with a set of generators, , encodes how the chosen generating elements operate (by multiplication) on the elements of the group.
Definition
Given a group, , and a set of generators, (e.g. a finitely generated group if is a finite set), which we regard as a subset of the underlying set of , we can form a directed graph with the elements of as the vertices and with its edges labelled (some people say ‘coloured’) by the elements of with an edge joining a vertex, , to the vertex labelled by
This graph is called the Cayley graph of the group, , relative to the set of generators.
The metric induced from corresponding graph distance is also called the word metric on the group with respect to its generators .
Examples
For the symmetric group
Example
The symmetric group may be generated from, in particular:
-
all transposition permutations – the corresponding Cayley graph distance is the original Cayley distance;
-
the adjacent transpositions – the corresponding Cayley graph distance is known as the Kendall tau distance.
Specifically:
Example
(Cayley graph of Sym(3))
The following is the Cayley graph of the symmetric groups on 3 elements, , with edges corresponding to any transposition (not necessarily adjacent), hence whose graph distance is the Cayley distance:
Example
The Cayley graph of the symmetric group with edges for transpositions looks as follows:
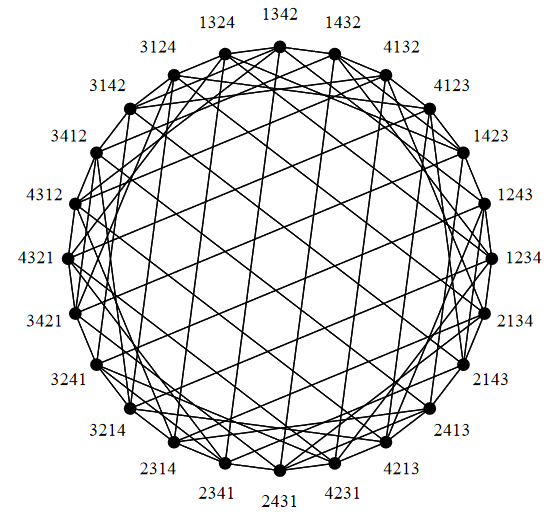
graphics from Kaski 02, p. 17
Example
Consider one of the standard presentations of the symmetric group , . Write , , .
The Cayley graph is easy to draw. There are two triangles corresponding to and to its translate by , , flipping the orientation of the second, and three 2-cycles, , and .
To understand the geometric significance of this graph we compare the algebraic information in the presentation with the homotopical information in the graph (considered as a CW-complex).
Looking at the presentation it leads to a free group, , on the generators, and , so is free of rank 2, but the normal closure of the relations is a subgroup of , so it must be free as well, by the Nielsen-Schreier theorem. Its rank will be 7, given by the Schreier index formula.
Looked at geometrically, this will be the fundamental group of the Cayley graph, of the presentation. This group is free on generators corresponding to edges outside a maximal tree, and, of course, there are 7 of these.
Related entries
References
General
Textbooks accounts:
-
Clara Löh, Section II.3 of : Geometric Group Theory, Springer 2017 (doi:10.1007/978-3-319-72254-2, pdf)
-
Cornelia Druţu, Michael Kapovich, Section 7.9 of: Geometric group theory, Colloquium Publications 63, AMS 2018 (ISBN:978-1-4704-1104-6, pdf)
Review:
- Elena Konstantinova, Some problems on Cayley graphs, Linear Algebra and its Applications Volume 429, Issues 11–12, 1 December 2008, Pages 2754-2769 (doi:10.1016/j.laa.2008.05.010)
See also:
- Wikipedia, Cayley graph
Discussion in homotopy type theory/univalent foundations of mathematics:
- Marc Bezem, Ulrik Buchholtz, Pierre Cagne, Bjørn Ian Dundas, Daniel R. Grayson: Def. 6.3.4 in: Symmetry (2021) [pdf]
Spectra
Discussion of Cayley graph spectra:
-
László Lovász, Spectra of graphs with transitive groups, Period. Math. Hungar., 6(2):191–195,1975 (doi:10.1007/BF02018821, pdf)
-
László Babai, Spectra of Cayley graphs, Journal of Combinatorial Theory, Series B Volume 27, Issue 2, October 1979, Pages 180-189 (doi:10.1016/0095-8956(79)90079-0)
-
Petteri Kaski, Eigenvectors and spectra of Cayley graphs, 2002 (pdf, pdf)
-
Briana Foster-Greenwood, Cathy Kriloff, Spectra of Cayley graphs of complex reflection groups, J. Algebraic Combin., 44(1):33–57, 2016 (arXiv:1502.07392, doi:10.1007/s10801-015-0652-8)
-
Xiaogang Liu, Sanming Zhou, Eigenvalues of Cayley graphs (arXiv:1809.09829)
-
Farzaneh Nowroozi, Modjtaba Ghorbani, On the spectrum of Cayley graphs via character table, Journal of Mathematical NanoScience, Volume 4, 1-2 (2014) (doi:10.22061/jmns.2014.477 pdf)
Distance on Cayley graphs
On graph distances in Cayley graphs (generalizing the Cayley distance for the symmetric group):
For symmetric groups (permutations):
-
Farzad Farnoud (Hassanzadeh), Lili Su, Gregory J. Puleo, Olgica Milenkovic, Computing Similarity Distances Between Rankings, Discrete Applied Mathematics Volume 232, 11 December 2017, Pages 157-175 (doi:10.1016/j.dam.2017.07.038, pdf, pdf)
-
Mohammad Hossein Ghaffri, Zohreh Mostaghim, Distance in Cayley graphs on permutations generated by cycles, Transactions on Combinatorics, Vol 6 No. 3 (2017) (pdf)
Last revised on January 17, 2023 at 16:05:02. See the history of this page for a list of all contributions to it.