nLab Cardy condition
Context
Functorial quantum field theory
Contents
Idea
The Cardy condition is part of the sewing constraint consistency condition on data that gives an open-closed 2d CFT or 2d TQFT.
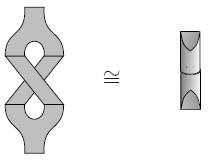
It is the algebraic reflection of the fact that the following two cobordisms are equivalent (as topological as well as as conformal cobordisms):
-
an open string coming in, closing to a closed string and then opening up again to an open string (the “zip-unzip cobordism”);
-
an open string coming in, splitting into two open strings, these crossing each other (with the endpoints of one of them at the same time making a full rotation), then both merging again to one open string.
(e.g. Lauda-Pfeiffer 05 (3.44), Kong 06, figure 3)
For instance in the classification of open-closed 2d TQFT with coefficients in Vect via Frobenius algebras, this means that for the Frobenius algebra of open string states and for the commutative Frobenius algebra of closed string states, then the canonical linear function
is equal to the canonical map
where is the coproduct, the product and the braiding (e.g. Lauda-Pfeiffer 05 (2.14)).
Related concepts
References
Discussion in 2d TQFT includes
-
Aaron Lauda, Hendryk Pfeiffer (2005), Open-closed strings: two-dimensional extended TQFTs and Frobenius algebras, Topology Appl. 155, 623-666. (arXiv:0510664)
-
Gregory W. Moore, Graeme Segal (2006), D-branes and K-theory in 2D topological field theory. (arXiv:hep-th/0609042)
-
Gregory W. Moore, Graeme Segal (2002), Lectures on Branes, K-theory and RR Charges. Lecture notes from the Clay Institute School on Geometry and String Theory held at the Isaac Newton Institute, Cambridge, UK. Available here; related notes from the ITP Miniprogram ‘The Duality Workshop’ at Santa Barbara available here.
Discussion in 2d CFT includes
- Liang Kong, Cardy condition for open-closed field algebras (arXiv:math/0612255)
Last revised on August 5, 2023 at 21:23:58. See the history of this page for a list of all contributions to it.