nLab C2-equivariant homotopy groups of spheres

Idea

$C_2$-equivariant homotopy groups of spheres are particularly amenable to study because they are computed in a range by $\mathbb{R}$-motivic homotopy groups via real Betti realization with its Galois action;

this is special to $C_2$ among finite groups, since the Artin-Schreier theorem implies that it is the only nontrivial finite group occurring as an absolute Galois groups. (…)

$\mathrm{RO}(G)$-graded vs Mackey functor homotopy groups

In general, for all real orthogonal virtual $G$-representations, we have a cofiber sequence of $G$-spectra

$$S(V)_+ \rightarrow D(V)_+ \rightarrow S^V;$$

In the case $V = \sigma$, we find that $S(V) = C_{2,+}$; hence there is a natural long exact sequence in stable homotopy in the motivic grading $\pi_{s,c}^{C_2}X \coloneqq \pi_{c + (s-c)\sigma}^{C_2} X$, this reads as

In particular, the five lemma combined with the equivariant Whitehead theorem then proves the following (see Prop 3.2 of Guillou-Isaksen 24).

Proposition

A map of $C_2$-spectra induces an isomorphism on $\mathrm{RO}(C_2)$-graded homotopy groups if and only if it induces an isomorphism on $\mathbb{Z}$-graded mackey functor homotopy groups.

The corresponding theorem is seldom true for other groups, since every other group attains two dimensional irreducible real orthogonal $G$-representations, whose compactifications will not be cofibers of $G$-sets. For instance, a counterexample due to Clover May in the case $G = C_3$ appears as Ex. 3.1 of Guillou-Isaksen 24.

Relation to motivic homotopy groups

The following diagram appears on page 3 of Guillou-Isaksen 24.

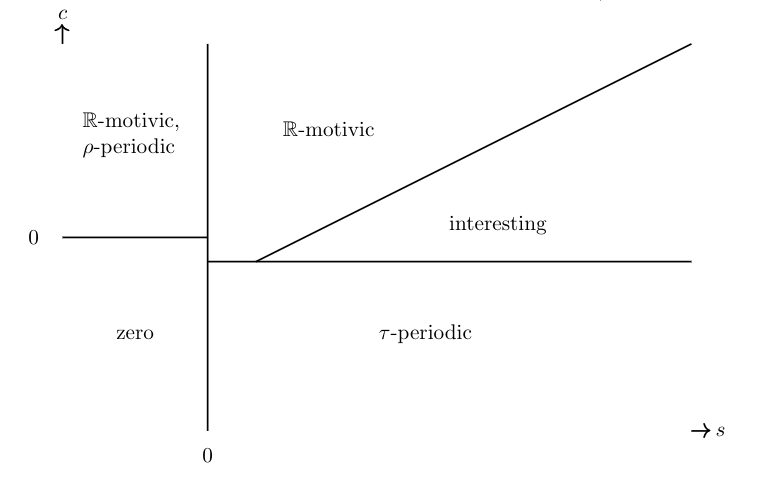
In this section, we will explain the regions. Explicitly:

• The region $c \gt \frac{1}{2}s - 5$ is described in Theorem

• (…)

The region $c \gt \frac{1}{2}s - 5$

In Heller-Ormsby 14, given a finite Galois extension $L/k$ with Galois group $G$, a symmetric monoidal functor

$$c_{\mathbb{C}/\mathbb{R}}^*:\mathrm{Sp}_{G} \rightarrow \mathrm{SH}_k$$

is constructed, which when evaluated on the endomorphism of the unit, yields the ring homomophism $A(G) \rightarrow GW(k)$ of Dress relating the Burnside ring to the Grothendieck-Witt ring?.

The following theorem is Theorem 1.1 of Heller-Ormsby 17 (with image shown in Heller-Ormsby 14).

Theorem

If $k$ is a real closed field and $L = k[i]$ its algebraic closure, then the functor

$$c_{L/k}^*:\mathrm{Sp}_{C_2} \rightarrow \mathrm{SH}_k$$

is a fully faithful symmetric left adjoint whose image is generated under tensor products and colimits by finite etale $k$-algebras.

This yields the corollary that $\pi^{\mathbb{R}}_{s,c} \rightarrow \pi^{C_2}_{s,c}$ is an isomorphism in degrees satisfying $s \geq c$ and $c \geq \frac{2}{3}s - 5/3$. (Thm 3.11 Heller-Ormsby).

By relating the $\mathbb{R}$-motivic and $C_2$-equivariant Adams $E_\infty$-pages, Belmont-Guillou-Isaksen 21 improved this to the following to the following.

Theorem

The map $\pi^{\mathbb{R}}_{s,c}(\mathbb{S}_{\mathbb{R}})^{\wedge}_{2,\eta} \rightarrow \pi_{s,c}(\mathbb{S}_{C_2})_2^{\wedge}$ is

1. an injection if $s = 2c + 5$, and

2. an isomorphism if $s \lt 2c + 5$ and $(s,c) \neq (0,-2)$.

The region $s \geq 0, c \leq -2$

Due to Bredon 67, as recalled e.g. in section 3.3 of Guillou-Isaksen 24, when $c \leq -2$ and $s \geq 0$, there are periodicity isomorphisms which recognize negative coweight $C_2$-equivariant homotopy groups as $\rho$-power torsion subgroups of positive-coweight groups. (…)

The region $(s,c) \leq (-1,-1)$

The spectral Mackey functor theorem quickly shows that any map $S^{-n - m\sigma} \rightarrow S^0$ is nullhomotopic when $n,m \in \mathbb{Z}_{\gt 0}$.

The region $-1 \leq c \leq \frac{s-5}{2}$ for small $s$

(…)

Related concepts

• equivariant homotopy group

References

• Glen Bredon, Equivariant Stable Stems, (1967) (pdf)

• Jeremiah Heller?, Kyle Ormsby?, Galois equivariance and stable motivic homotopy theory, (2014) (arXiv:1401.4728)

• Jeremiah Heller?, Kyle Ormsby?, The stable Galois correspondence for real closed fields, (2016) (arXiv:1701.09099)

• Eva Belmont?, Bertrand Guillou, Daniel Isaksen, $C_2$-equivariant and $\mathbb{R}$-motivic stable stems, II, (2020) (arXiv:2001.02251v1)

• Bertrand Guillou, Daniel Isaksen, $C_2$-Equivariant Stable Stems, (2024) (arXiv:2404.14627)