nLab subspace topology
Context
Topology
topology (point-set topology, point-free topology)
see also differential topology, algebraic topology, functional analysis and topological homotopy theory
Basic concepts
-
fiber space, space attachment
Extra stuff, structure, properties
-
Kolmogorov space, Hausdorff space, regular space, normal space
-
sequentially compact, countably compact, locally compact, sigma-compact, paracompact, countably paracompact, strongly compact
Examples
Basic statements
-
closed subspaces of compact Hausdorff spaces are equivalently compact subspaces
-
open subspaces of compact Hausdorff spaces are locally compact
-
compact spaces equivalently have converging subnet of every net
-
continuous metric space valued function on compact metric space is uniformly continuous
-
paracompact Hausdorff spaces equivalently admit subordinate partitions of unity
-
injective proper maps to locally compact spaces are equivalently the closed embeddings
-
locally compact and second-countable spaces are sigma-compact
Theorems
Analysis Theorems
Contents
Definition
Definition
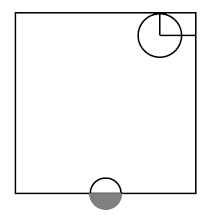
Let be a topological space, and let be a subset of its underlying set. Then the corresponding topological subspace has as its underlying set, and its open subsets are those subsets of which arise as restrictions of open subsets of (i.e. intersections of open subsets of with ):
In other words, is the smallest topology on such that the inclusion is continuous (the initial topology on that map).
The picture on the right shows two open subsets inside the square, regarded as a topological subspace of the plane :
graphics grabbed from Munkres 75
The pair is then said to be a topological subspace of . The induced topology is for that reason sometimes called the subspace topology on .
A continuous function that factors as a homeomorphism onto its image equipped with the subspace topology is called an embedding of topological spaces. Such a map is referred to as a subspace inclusion.
A property of topological spaces is said to be hereditary if its satisfaction for a topological space implies its satisfaction for all topological subspaces of .
Examples
- The open subsets of a closed interval regarded as a topological subspace of the real line equipped with its Euclidean metric topology is generated from the sub-base .

The image on the right shows open subsets in the closed square , regarded as a topological subspace of the Euclidean plane
- A subset of a metric space equipped with its induced metric is a subspace with respect to the corresponding metric topologies.
Properties
Universal property
Proposition
(universal property of subspace topology)
Let be an injective continuous function between topological spaces. Then this is a subspace inclusion (Def. ) precisely if it satisfies the following universal property:
-
For any topological space, a function (of underlying sets) is continuous precisely if the composition is continuous as a function to :
The elementary proof is spelled out, for instance, in Terilla 14, theorem 1. Of course this is just another way to speak of the initial topology.
The universal characterization of Prop. lends itself to formalization via axioms for cohesion:
Definition
(sharp modality on topological spaces)
Let
be the pair of adjoint functors given by sending a topological space to its underlying set , and by equipping a set with the codiscrete topology making it a codiscrete space .
Write
for the induced modal operator on Top (sharp modality). We write
for the unit morphism of this adjunction.
Notice that this means that for any topological space , every function of underlying sets
is continuous functions, hence that continuous functions into are in natural bijection to underlying functions of sets. This is the statement of the adjunction hom-isomorphism:
Proposition
Let be an injective continuous function between topological spaces. Then this is a subspace inclusion (Def. ) precisely if its naturality square of the -unit (Def. )
is a pullback square.
Proof
By the universal property of a pullback/fiber product and the nature of , we have precisely if continuous functions out of some topological space into are in natural bijection with continuous functions whose underlying function factors through the underlying function of . This implies the statement by Prop. .
Remark
(formulation in cohesive homotopy type theory)
The pullback square of the -unit in Prop. should correspond (after generalizing from topological spaces to suitable topological ∞-groupoids) to the categorical semantics of what in cohesive homotopy type theory is the statement that the characteristic function
to the universe of propositions factors through the universe of sharp-modal types. In this form topological subspace inclusions are characterized in Shulman 15, Remark 3.14.
General
A subspace is closed if is closed as a subset of (or if is a closed map), and is open if is open as a subset of (or if is an open map).
Proposition
Topological subspace inclusions (topological embedding) are precisely the regular monomorphisms in the category Top of all topological spaces.
For example, the equalizer of two maps in Top is computed as the equalizer at the underlying-set level, equipped with the subspace topology.
Lemma
The pushout in Top of any (closed/open) subspace along any continuous function ,
is a (closed/open) subspace .
Proof
Since is faithful, we have that monos are reflected by ; also monos and pushouts are preserved by since has both a left adjoint and a right adjoint. In , the pushout of a mono along any map is a mono, so we conclude is monic in . Furthermore, such a pushout diagram in is also a pullback, so that we have the Beck-Chevalley equality (where is the direct image map between power sets, and is the inverse image map).
To prove that is a subspace, let be any open set. Then there exists open such that because is a subspace inclusion. If and are the maps to Sierpinski space that classify these open sets, then by the universal property of the pushout, there exists a unique continuous map which extends the pair of maps . It follows that , so that is a subspace inclusion.
If moreover is an open inclusion, then for any open we have that (since is monic) and (by Beck-Chevalley) is open in . By the definition of the topology on , it follows that is open, so that is an open inclusion. The same proof, replacing the word “open” with the word “closed” throughout, shows that the pushout of a closed inclusion is a closed inclusion .
A similar (but even simpler) line of argument establishes the following result.
Lemma
Let be an ordinal, viewed as a preorder category, and let be a functor that preserves directed colimits. Then if is a (closed/open) subspace inclusion for each morphism of , then the canonical map is also a (closed/open) inclusion.
Variations
There is also a notion of a Grothendieck topology induced along a functor from a Grothendieck topology on another category (actually the input can be a somewhat more general coverage, then the topology induced along the identity functor will serve as a sort of a completion). (this will be explained later).
A topology may be induced by more than a function other than a subset inclusion, or indeed by a family of functions out of (not necessarily all with the same target). However, the term ‘induced topology’ is often (usually?) restricted to subspaces; the general concept is called a weak topology. (This construction can be done in any topological concrete category; in this generality it is often called an initial structure for a source.) The dual construction (involving functions to ) is a strong topology (or final structure for a sink); an example is the quotient topology on a quotient space.
Related concepts
examples of universal constructions of topological spaces:
References
-
Nicolas Bourbaki, Elements of Mathematics – General topology, 1971, 1990
-
James Munkres, Topology, Prentice Hall (1975, 2000)
-
John Terilla, Notes on categories, the subspace topology and the product topology 2014 (pdf)
-
Mike Shulman, Brouwer’s fixed-point theorem in real-cohesive homotopy type theory, Mathematical Structures in Computer Science Vol 28 (6) (2018): 856-941 (arXiv:1509.07584, doi:10.1017/S0960129517000147)
Last revised on December 1, 2019 at 06:42:12. See the history of this page for a list of all contributions to it.