nLab horn
Context
Homotopy theory
homotopy theory, (∞,1)-category theory, homotopy type theory
flavors: stable, equivariant, rational, p-adic, proper, geometric, cohesive, directed…
models: topological, simplicial, localic, …
see also algebraic topology
Introductions
Definitions
Paths and cylinders
Homotopy groups
Basic facts
Theorems
Contents
Idea
In simplicial homotopy theory a horn of a simplex is a simplicial incarnation of the notion of a boundary segment (as opposed to the full boundary) of a cell.
Specifically, the th horn of the -dimensional simplex (defined for , see Rem. ) is the simplicial set obtained from the boundary of the n-simplex of the standard simplicial n-simplex by discarding its th face.
The property of a morphism of simplicial set to have the right lifting property against the inclusions of horns into their simplices (have “horn fillers”) characterizes the basic types of fibrations and fibrant objects in simplicial homotopy theory:
-
Kan fibrations (hence Kan complexes, when over the point) are characterized as having the right lifting property against all horns;
-
left/right Kan fibrations are characterized as having the right lifting property against all horns except possibly the first/last horn inclusion in each dimension, respectively;
-
quasi-categories are characterized as having the right lifting property against all horns except possibly the first and last horn inclusion in each dimension, respectively.
Specifically, Kan fibrations are the simplicial analog of Serre fibrations (in a precise sense so under the Quillen equivalence between the classical model structure on simplicial sets and on topological spaces) and under this correspondence the horn inclusions into the th simplex correspond to the inclusion of the -dimensional topological disk into its cylinder:
as both are the generating cofibrations in their respective model categories (on sSet, on Top, respectively).
Definition
Let
denote the standard simplicial -simplex in SimpSet.
Definition
(horns)
For all with and , the -horn or -box is the sub-simplicial set
which is the union of all faces except the th one.
This is called an outer horn if or , otherwise it is an inner horn.
Remark
Since sSet is a presheaf topos, unions of subobjects make sense and they are calculated objectwise, thus in this case dimensionwise. This way it becomes clear what the structure of a horn as a functor must therefore be: it takes to the collection of ordinal maps which factor through some coface map which is not the th one.
Remark
(the 0-simplex has no horns)
Beware that any would-be horn of the 0-simplex (whose boundary is the empty simplicial set) is ex-cluded in Def. : The 0-simplex has no horn.
This is not a matter of convention if one sticks to the usual definition of Kan fibration as having right lifting against all horns: In particular one must not declare a would-be horn of the 0-simplex to be itself the empty simplicial set, as that would make the nerve of the empty groupoid fail to be a Kan complex (Def. ).
Conversely, the fact that every horn is inhabited means (see also this Example) that any morphism out of the empty simplicial set (an empty bundle ) is a Kan fibration (Def. ).
This is in contrast to the situation for acyclic Kan fibrations, see there.
Examples
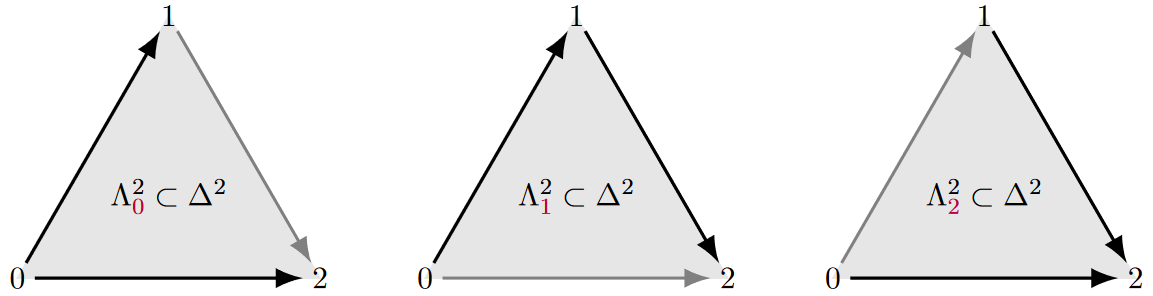
Example
The inner horn of the 2-simplex
with boundary
looks like
The two outer horns look like
and
respectively.
Lifting against horn inclusion
Definition
(Kan fibration)
A Kan fibration is a morphism of simplicial sets which has the right lifting property with respect to all horn inclusions .
Definition
(Kan complex)
A Kan complex is a simplicial set in which “all horns have fillers”: a simplicial set for which the morphism to the point is a Kan fibration (Def. ).
Definition
(quasi-category)
A quasi-category is a simplicial set in which all inner horns have fillers, hence such that the morphism to the point is an inner fibration.
Related concepts
-
The boundary of a simplex is the union of its faces.
-
The spine of a simplex is the union of all its generating 1-cells.
References
See the references at simplicial homotopy theory.
Last revised on February 5, 2024 at 12:30:45. See the history of this page for a list of all contributions to it.